47. Уравнение прямой в пространстве, проходящей через две данные точки.

Пусть прямая проходит через точки . Составим каноническое уравнение прямой, проходящей через эти точки. Для этого найдем направляющий вектор, за который примем вектор . , , Используя каноническое уравнение прямой и рассматривая ее как прямую, проходящую через точку 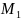, получим: .

48. Прямая как линия пересечения двух плоскостей.

Пусть даны две плоскости , причем они не параллельны, т. е. Тогда прямую можно рассматривать как прямую пересечения двух плоскостей. . Общее уравнение прямой линии в пространстве: Так как прямая принадлежит плоскости , а – вектор нормали, то . . Тогда за вектор естественно принять вектор S, равный векторному произведению векторов и 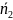. . - координаты базисного вектора, – коэффициенты плоскости , – коэффициенты плоскости . За точку на прямой можно выбрать любую точку, координаты которой удовлетворяют общим уравнениям прямой, т. е. являются решениями системы уравнений (1). Но так как уравнений два, а неизвестных – три, то такая система имеет бесчисленное число решений. Тогда одна из неизвестных принимается за параметр или приравнивается к нулю и находятся две другие координаты точки прямой.

49. Окружность. Определение. Каноническое уравнение.

Окружность – это множество всех точек плоскости, равноудаленных от заданной точки, называемой центром. Уравнение окружности с центром в точке с координатами и радиусом R: .

50. Эллипс. Определение. Каноническое уравнение. Свойства.

Эллипс – множество всех точек плоскости, для каждой из которых сумма расстояний до двух заданных фиксированных точек, называемых фокусами, есть величина постоянная. Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса): , где a и b – полуоси эллипса; – фокусы эллипса, если . . Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Эксцентриситет вычисляется по формуле 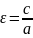. Для эллипса . Все точки эллипса лежат в прямоугольнике.

51. Гипербола. Определение. Каноническое уравнение. Свойства.

Гипербола – множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух заданных фиксированных точек, называемых фокусами, есть величина постоянная. Каноническое уравнение гиперболы (оси координат совпадают с осями гиперболы): , где a, b – соответственно действительная и мнимая полуоси гиперболы, – фокусы гиперболы ( . . Эксцентриситет вычисляется по формуле ; для гиперболы . Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах - ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.