8. Ранг матрицы. Нахождение ранга матрицы.

Рангом матрицы называется наивысший порядок миноров данной матрицы, отличных от нуля. Обозначение: . Чтобы найти ранг матрицы, необходимо найти ненулевой элемент матрицы, вычислить миноры второго порядка, окаймляющие выбранный элемент. Если среди них имеется отличный от нуля, необходимо рассмотреть все миноры третьего порядка, окаймляющие какой-нибудь минор второго порядка, не равный нулю. Продолжать так до тех пор, пока все миноры, окаймляющие ненулевой минор r-го порядка, не будут равны нулю. В этом случае ранг равен r. Есть и другой способ: привести матрицу к ступенчатому виду с помощью элементарных преобразований, тогда число строк будет равно рангу.

9. Системы линейных алгебраических уравнений.

Уравнение называется линейным, если все неизвестные входят в него в 1-ой степени и отсутствует произведение неизвестных. Система уравнений вида называется системой m линейных уравнений с n неизвестными, где числа - коэффициенты системы, – свободные члены. Система называется совместной, если имеет решение, и несовместной, если решений нет. Система называется определенной, если имеет 1 решение, и неопределенной, если множество решений. Системы называются равносильными, если имеют одинаковые решения.

10. Решение систем линейных алгебраических уравнений методом Гаусса.

Метод Гаусса заключается в том, что с помощью элементарных преобразований система приводится к равносильной системе ступенчатого вида («прямой ход»), из которой последовательно, начиная с последних переменных, находятся остальные переменные («обратный ход»). Преобразования удобнее выполнять не над уравнениями системы, а над ее расширенной матрицей. Если r=n, то система имеет единственное решение, если r<n, то множество решений (r – ранг системы, n – число неизвестных). Во втором случае неизвестные объявляются главными, а остальные – независимыми, они могут принимать любые значения.

11. Нахождение решения системы линейных алгебраических уравнений по формуле Крамера.

Теорема Крамера. Если в системе n уравнений с n неизвестными определитель отличен от нуля (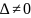 ), то система совместна и имеет единственное решение, определяемое по формуле: , где – определитель, полученный из путем замены i-го столбца столбцом свободных членов (1<i<n). Если определитель равен нулю ( ), возможны два случая: 1) если хотя бы один из определителей отличен от нуля, система не имеет решения; 2) если все равны 0, система имеет бесчисленное множество решений.

12. Нахождение решения системы линейных алгебраических уравнений методом обратной матрицы.

В матричной форме система n линейных уравнений с n неизвестными имеет вид: A= , X= , B= . Здесь А – матрица коэффициентов системы, называемая обратной матрицей, Х – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Если определитель основной матрицы не равен нулю, то система совместна и ее единственное решение находится по формуле: . Если система вырождена, т. е. , то данную систему матричным методом решить нельзя.