29. Матрица линейного оператора.

Пусть – базис линейного пространства L, в котором действует линейный оператор φ. Подействуем оператором φ на базисные векторы 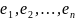и разложим образы базисных векторов по тому же базису:

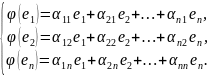
Матрицей линейного оператора φ в базисе называется квадратная матрица n-го порядка 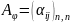, i-ый столбец которой состоит из координат вектора 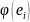в базисе , т. е.

30. Собственные значения и собственные векторы линейных операторов.

Пусть линейный оператор φ действует в линейном пространстве L и имеет в некотором базисе этого пространства матрицу 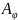. Ненулевой вектор x из L называется собственным вектором линейного оператора φ, если существует число 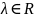такое, что . Число λ называется при этом собственным значением оператора φ. Говорят также, что собственный вектор x отвечает (или соответствует) собственному значению λ.

31. Собственные значения квадратных матриц.

Собственное значение λ линейного оператора φ называется также собственным значением матрицы . Во многих разделах математики и ее экономических приложений рассматриваются именно собственные значения матриц, вне их связи с линейными операторами. В базисе из собственных векторов матрица оператора φ имеет диагональный вид, где 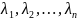– собственные значения оператора φ:

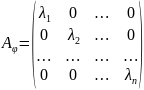
32. Квадратичные формы, их матрицы в данном базисе.

Квадратичной формой 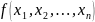от n переменных называется многочлен с действительными коэффициентами , каждый член 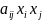которого имеет вторую степень, т. е. многочлен вида 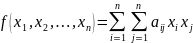, где числа (коэффициенты квадратичной формы) удовлетворяют условию . Матрица 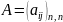, составленная из коэффициентов квадратичной формы, называется матрицей квадратичной формы, а ее ранг – рангом квадратичной формы.

33. Приведение квадратичной формы к нормальному виду методом Лагранжа.

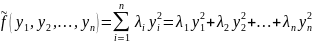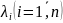Любую квадратичную форму невырожденным преобразованием X=PY можно привести к эквивалентной ей форме вида . Это выражение называется каноническим видом квадратичной формы (оно не содержит попарных произведений переменных), а числа – ее каноническими коэффициентами. Метод Лагранжа состоит в последовательном выделении в квадратичной форме полных квадратов по каждой переменной. При этом, если в квадратичной форме нет членов с квадратами переменных, т. е. в ней все коэффициенты 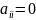, то сначала добиваются, чтобы в квадратичной форме появились члены с квадратами переменных.

34. Приведение квадратичной формы к каноническому виду при помощи ортогонального преобразования.

Любую квадратичную форму невырожденным преобразованием X=PY можно привести к эквивалентной ей форме вида . Это выражение называется каноническим видом квадратичной формы (оно не содержит попарных произведений переменных), а числа – ее каноническими коэффициентами.

Преобразование переменных X=PY называется ортогональным, если его матрица P ортогональна, т. е. . Для любой квадратичной формы 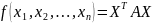существует ортогональное преобразование X=PY, приводящее ее к каноническому виду . При этом – собственные значения матрицы A, а столбцы матрицы P – попарно ортогональные нормированные собственные векторы матрицы A.