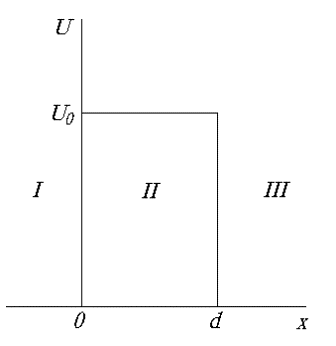25. Квантование момента импульса

Момент импульса М является одной из важнейших характеристик движения. Его значение связано с тем, что М сохраняется, если система изолирована или движет­ся в центральном силовом поле. Однако в квантовой теории мо­мент импульса существенно отличается от классического. А именно, модуль момента импульса может быть задан сколь угодно точно только с одной из проекций, например, М_z. Дру­гие две проекции оказываются полностью неопределенными.

Это означает, что направление момента М в пространстве является неопределенным. Наглядно подобную ситуацию можно попы­таться представить так: вектор М как-то ♦ размазан» по образующим конуса, ось кото­рого совпадает с направлением координатной оси Z (рис. 5.1). В этом случае вполне опреде­ленное значение имеет лишь проекция М_г. Другие две проекции, М_х и М_у, оказываются полностью неопределенными.

26. Принцип суперпозиции

Рассмотрим метод определения модуля и направления вектора напряженности Е в каж­дой точке электростатического поля, создаваемого системой неподвижных зарядов Q₁, Q₂, ..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил, т. е. результирующая сила F, дейст­вующая со стороны поля на пробный заряд Q₀, равна векторной сумме сил F_i, приложенных к нему со стороны каждого из зарядов Q_i: (80.1)

Согласно (79.1), F = Q₀E и F_i = Q₀Е_i, где Е—напряженность результирующего поля, а Е_i — напряженность поля, создаваемого зарядом Q_i. Подставляя последние выраже­ния в (80.1), получаем (80.2)

Формула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя.

27) Прохождение частиц через потенциальный барьер.

Туннельный эффект

Рис. 1.7. Потенциальный барьер конечной ширины

Рассмотрим поведение квантово-механической частицы при прохождении через потенциальный барьер конечной ширины (рис.1.7). Ограничимся рассмотрением одномерной задачи, когда ось x параллельна движению частицы. В каждой из трех областей I, II и III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Эта задача моделирует многие физически важные явления, например, выход электронов из металлов, распад атомных ядер и др.

          Уравнение Шредингера в этом случае будет иметь вид   (1.40)

В области I уравнение (1.40) будет иметь вид

  (1.41)

  Для области II уравнение Шредингера запишется в виде

  (1.45)

Уравнение Шредингера для микрочастицы в области III будет иметь тот же вид, что и в области I. Общее решение для этой области будет отличаться от решения (1.44) тем, что в области III нет отраженной волны (b₃ = 0)

  (1.48)

В случае потенциального барьера произвольной формы,(рис. 1.8)

Рис. 1.8. Потенциальный барьер произвольной формы

проницаемость барьера выражается приближенной формулой (1.53)

Таким образом, квантово-механической частице для преодоления потенциального барьера необязательно иметь энергию больше, чем высота барьера. Она как бы проходит через “туннель” (заштрихованная область на рис. 1.8), расположенном на высоте E, где E - полная энергия микрочастицы. В связи с этим рассмотренное явление называют туннельным эффектом.