20.Гипотеза де – Бройля.

В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами. Если фотон обладает энергией и импульсом, то и частица (например электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е. движение частицы можно рассматривать как движение волны.

Согласно квантовой механике, свободное движение частицы с массой m и импульсом (где υ – скорость частицы) можно представить как плоскую монохроматическую волну (волну де Бройля) с длиной волны

распространяющуюся в том же направлении (например в направлении оси х), в котором движется частица.

Зависимость волновой функции от координаты х даётся формулой

, где – волновое число, а волновой вектор направлен в сторону распространения волны или вдоль движения частицы:

Таким образом, волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны.

Поскольку кинетическая энергия сравнительно медленно движущейся частицы , то длину волны можно выразить и через энергию:

При взаимодействии частицы с некоторым объектом – с кристаллом, молекулой и т.п. – её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности дифракции частиц ничем не отличаются от закономерностей дифракции любых волн. Общим условием дифракции волн любой природы является соизмеримость длины падающей волны λ с расстоянием d между рассеивающими центрами:

21. Принцип неопределенности. По соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определен­ную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, p_у, p_z), причем неопределенности этих величин удовлетворяют условиям

, ,

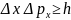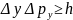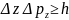
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.

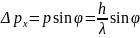
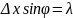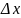, –ширина щели, – длина волны

При движении по траектории в любой момент времени с определенными значениями координат и скорости, соотношение неопределенностей:

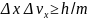
Cоотношение неопределенностей для энергии Е и времени t: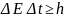 Е — неопределенность энергии некоторого состояния системы, t — промежуток времени, в течение которого оно существует. Следовательно, систе­ма, имеющая среднее время жизни t, не может быть охарактеризована определенным значением энергии; разброс энергии E=h/t возрастает с уменьшением среднего времени жизни.=>частота излученного фотона также должна иметь неопределенность  = E/h, т. е. линии спектра должны характеризо­ваться частотой, равной ± E/h.