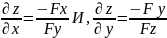16.Частные производные .Первый полный дифференциал. Его инвариантность

16) Частная производная. В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных. В явном виде частная производная функции f определяется следующим образом: Полным дифференциалом функции называется линейная (относительно и ) часть полного приращения функции: Инвариантность формы первого дифференциала

Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеем df(x0) = f'(x0)dx.Если x = φ(t) - дифференцируемая функция, то dx = φ'(t0)dt. Следовательно,

т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.

17) (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке . Одномерный случай: Пусть даны функции, определённые в окрестностях на числовой прямой,   где   и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

Замечание

В обозначениях Лейбница цепное правило для вычисления производной функции   где   

принимает следующий вид:

Инвариантность формы первого дифференциала

Дифференциал функции   в точке   имеет вид:

где   — дифференциал тождественного отображения  :

Пусть теперь  Тогда  , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет. Многомерный случай: Пусть даны функции   где   и   Пусть также эти функции дифференцируемы:   и   

Тогда их композиция тоже дифференцируема,

и её дифференциал имеет вид

В частности, матрица Якоби функции   

является произведением матриц Якоби функций   и 

Следствия

Якобиан композиции двух функций является произведением якобианов индивидуальных функций:

ля частных производных сложной функции справедливо

: Дифференцирование неявных функций. Ответ: Теорема существования и дифференцируемости функции, заданной неявно

Теорема 1. Пусть функция F(x,y) удовлетворяет условиям

F(x₀,y₀) = 0 ;

частные производные F'_x и F'_y непрерывны в некоторой окрестности точки (x₀,y₀) ;

F'_y(x₀,y₀) ≠ 0 .

Тогда

уравнение F(x,y) = 0 определяет неявно в некоторой окрестности точки x₀ единственную непрерывную функцию y(x) , удовлетворяющую условию y(x₀) = y₀ .

функция y(x) имеет производную, непрерывную в окрестности точки x₀ .

Выясним смысл условий теоремы.

Существование непрерывной неявной функции y = f(x) в окрестности точки (x₀, y₀) следует из теоремы существования, так как:

условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению F(x,y) = 0 ;

из условия 2 следует непрерывность функции F(x,y) в окрестности точки (x₀,y₀) , а из условия 3 — ее монотонность по y при каждом фиксированном x из этой окрестности.

Следовательно, условия 1–3 обеспечивают выполнение условий существования неявной функции y(x) , удовлетворяющей условию y(x₀) = y₀ и непрерывной в окрестности точки x₀ .

Производная функции, заданной неявно

Функция y(x) в окрестности точки x₀ обращает уравнение F(x,y) = 0 в тождество, т.е.

F(x,y(x)) ≡ 0. Дифференцируя это тождество, получaeм dF(x, y(x)) ≡ 0, а в силу инвариантности формы полного дифференциала имеем

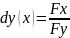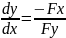F'_x · dx + F'_y · dy(x) ≡ 0 Отсюда получаем следующие формулы. Дифференциал функции, заданной неявно: dx Производная функции, заданной неявно: Теорема 1 обобщается для неявных функций любого числа переменных. Например:

Теорема 2. Пусть функция F(x,y,z) = 0 удовлетворяет условиям

F(x₀,y₀,z₀) = 0 ;

частные производные F'_x , F'_y и F'_z непрерывны в некоторой окрестности точки (x₀,y₀,z₀) ;

F'_z(x₀,y₀,z₀) ≠ 0 .

Тогда

уравнение F(x,y,z) = 0 определяет неявно в некоторой окрестности точки (x₀,y₀) единственную непрерывную функцию z(x,y) , удовлетворяющую условию z(x₀,y₀) = z₀ ;

функция z(x,y) имеет непрерывные частные производные в окрестности точки (x₀,y₀) , вычисляемые по формулам: