1)Последовательности.Предел последовательности . Постоянное число а называется пределом переменной величины х , если для каждого наперед заданного произвольно малого положительного числа E можно указать такое значение переменной х , что все последующие значения переменной будут удовлетворять неравенству |x-a|< E. Числовая последовательность -  функция  вида y = f(x), x О N,где N – множество натуральных чисел.

Числовая последовательность Х_n

называется сходящейся к числу а, ес-

ли разность междуХ_n

и а с ростом номера п становится как угодно малой

Точнее – если для любого заданного числа ε > 0 найдется номер N (E. ) такой, что при n N≥ (E.) выполняется соотношение |X_n-a|< E

При этом число а называется пределом последоват-ти x_n

Передел последовательности Если существует такое число A, что для любого (сколь угодно малого) положительного числа e найдется такое натуральное N (вообще говоря, зависящее от e), что для всех n і N будет выполнено неравенство |a_n – A| < e, то говорят, что последовательность {a_n} сходится и A – ее предел.

Обозначается это так:  .

2) Теория пределов последовательностей , арифметика пределов критерий Коши Критерий Коши последовательность a_n имеет конечный предел тогда и только тогда , когда для любого Е больше 0 существует Н такое что при н ,м больше Н выполняется |a_n-a_m|<E

Т: Если последовательность имеет конечный предел ,то он единственен

Док-во : Пусть a_n имеет два предела A≠B A>B возьмем E=(A-B)/ 1)Существует N₁ такое что при n>N1 |an-A|<E 2)Существует N2 такое что n>N2 |an-B|<E (рис.на листе)Возьмем N= max(N1,N2) тогда при n>N выполняются оба неравенства одновременно .Что невозможно

T:пусть an>0 при всех n и имеет 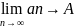тогда

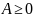
Арифметика пределов

1.Пусть существует an и bn причем 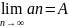|A|<∞

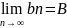|B|<∞

Тогда 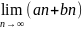=A+B

=A*B

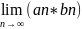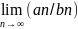=A/B B≠0

3)Признаки существования предела последовательности. Пусть an- монотонно не убывает и ограничена сверху. тогда an имеет конечный предел. Т: пусть даны an; bn;cn так что выполняется : 1.an≤bn<cn для всех n

2.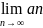 =. =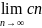A

Т огда существует .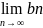 =. (док-во на листе)

4)Бб и бм последовательности

О: Послед. Наз. БМ если предел = 0

1.сумма бм является бм

2.произведение бм является бм

3.произведение бм и ограниченной является бм

О:Ф-ция F(x) стремится к бесконечности при х→а т.е. явл ББ величиной ,если для каждого положительного числа М, как бы оно не было велико , можно найти такое число 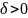, что для всех значений х отличных от а , удовл условию |x-a|<δ имеет место неравенство |f(x)|>M

Послед называется бб если предел an=-∞

5)Предел ф-ции, арифметика пределов. Критерий Коши

Предел ф-ции Число А называется пределом функции f если для всех E>0 выполняется, что |f(E)-A)|<E

Арифметика пределов

1.Пусть существует an и bn причем |A|<∞

|B|<∞

Тогда =A+B

=A*B

=A/B B≠0

Критерий Коши последовательность a_n имеет конечный предел тогда и только тогда , когда для любого Е больше 0 существует Н такое что при н ,м больше Н выполняется |a_n-a_m|<E

6) Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при .

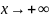Последовательность a_n называется бесконечно большой, если .

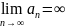Функция называется бесконечно большой в окрестности точки x₀, если .

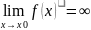Функция называется бесконечно большой на бесконечности, если 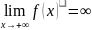либо .

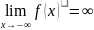7) Замечательные пределы, число е. Числом «е» называется такое число, для которого будет справедливо равенство 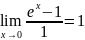. Числом «е» также называют основание такой показательной функции график которой в точке (0,1) образует с осью ох угол Пи/4.

Замечательный степенной предел 

Замечательный степенной предел 

Замечательный показательно-степенной предел

Замечательный тригонометрический предел

8) Функции, непрерывные в точке. Классификация разрывов.

функция f(x) называется непрерывной в точке x₀, если выполняется

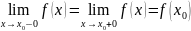
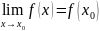
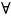E>0 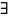δ>0 xє(х₀-δ, х₀+δ) |f(x) - f(x₀)|<0 f(x₀+∆x) – f(x₀) = ∆f(x₀)

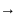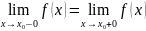Если в точке х сущ. оба предела, но предел f(x) x x₀+0 то х₀ – наз. точкой разрыва первого рода.

Все остальные точки разрыва 2-ого рода. Если х₀ – точка разрыва второго рода то хотя бы 1 предел не существует.

9) Свойства непрерывных функций (теорема о максимуме)

Теорема Веерштрасса. Если f(x) непрерывна на замкнутом промежутке [a,b], то на этом промежутке она достигает своего наибольшего и наименьшего значения. f(x)=x² xє(0,1) – не удовлетворяет т-ме Веерштрасса. f(x)=x² xє[0,1] – все ок!

10) Производная, ее геометрический и физический смысл. Техника дифференцирования.

f(a,b) возьмем на этом интервале х и ∆х в этих точках посчитаем f(x) и f(x+∆x)

∆f(x)= f(x+∆x)-f(x) ∆f(x)= f(x+∆x)-f(x)/∆х предел этого отношения при ∆х→0 называется производной от функции f по аргументу х f’(x)=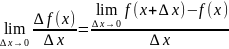

Если функция f:U(x₀)→R имеет конечную производную в точке x₀, то в окрестности U(x₀) её можно приблизить линейной функцией f_l(x)=f(x₀) + f’(x₀)(x-x₀). Функция f_l называется касательной к f в точке x₀. Число f’(x₀) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀. Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: C' = 0 x' = 1 (f+g)’=f’+g’ (fg)’=f’g+fg’ (Cf)’=Cf’ (f/g)’=f’g-fg’/g²…(g ≠ 0) (C/g)’=-Cg’/g² (g ≠ 0)