19)Выпуклость ф-ции и знак второй производной. Точки перегиба

О: ф-ция называется выпуклой вверх в точке М если в некоторой окрестности этой точки график находится ниже касательной к нему.

О: ф-ция называется выпуклой вниз в точке М если в некоторой окрестности этой точки график находится выше касательной к нему

Пусть f(x) имеет в некоторой окрестности точки х₀ вторую производную, причем она непрерывна в этой окрестности, для того чтобы f(x) была выпуклой вверх в точке х₀ достаточно что бы вторая производная была меньше нуля.

Док-во: напишем уравнение касательной через точку М

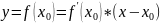
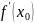-угловой коэф М=(х₀;F(x₀))

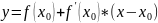(A)

Для 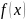напишем ф-лу Тэйлора второго порядка 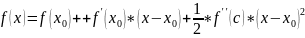(B)

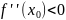
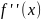-непрерывна в окрестности х₀ с €(Х₀;Х)значит отрицательна в некоторой окрестности точки Х₀ . Рассмотрим ф-лу Тэйлора в этой окрестности. Сравним ф-лы А и В в этой окресности f(x)<y

О:точка в которой выпуклость ф-ции меняет свой характер называется точкой перегиба

20)Необходимое и достаточное условия максимума (минимума) функции одной переменной

(необходимые условия экстремума).

Пусть задана функция z =z (x,y), (x,y) D. Точка M₀(x₀;y₀ D - точка локального экстремума.

Если в этой точке существуют z'_x и z'_y, то

Если в точке C₀ на провести касательную плоскость, то она пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.

Тогда в соответствии с геометрическим смыслом частных производных

(достаточные условия экстремума).

Пусть задана z =z (x,y), (x,y) D, которая имеет частные производные второго порядка в некоторой окрестности точки M₀(x₀,y₀) D. Причем M₀ - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:

Если:

21)Схема решения задач на глобальный и локальный минимум

Точки локального максимума (минимума)— значение переменной, при которой ф-ция достигает своей наибольшей (наименьшей) величины. Такие точки еще называются точками экстремума.

Глобальный максимум (минимум) ф-ции — наибольшее (наименьшее) значение функции при указанных ограничениях. Другое название — глобальные экстремумы.

1.Найти производную функции: f’(x).

2.Решить уравнение f’(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.

3.Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка [a; b]. Оставшиеся числа обозначим x₁, x₂, ..., x_n — их, как правило, будет немного.

4.Подставим концы отрезка [a; b] и точки x₁, x₂, ..., x_n в исходную функцию. Получим набор чисел f(a), f(b), f(x₁), f(x₂), ..., f(x_n), из которого выбираем наибольше или наименьшее значение — это и будет ответ.

22)Асимптоты ф-ции

О: прямая х=х₀ называется вертикальной асимптотой графика у=f(x) если выполняется хотя бы одно равенство

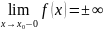
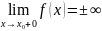
О: у=А называется горизонтальной асимптотой f(x)если вып. Хоть одно из равенств

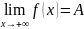
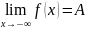
О: прямая у=Ах+В назыв. наклонной асимптотой если вып. Хоть одно из равенств

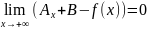
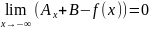
23)Общий план построения графиков и исследования ф-ций.

1.Описание области определения ф-ции.2.нахождение асимптот .3.Нахождение первой производной ,описание областей монотонности.4.Нахождение локального макс и мин .5.описание областей выпуклости и точек перегиба