29)Интегрирование тригонометрических ф-ций

Универсальная тригонометрическая подстановка дает возможность проинтегрировать всякую функцию вида

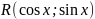
Рассмотрим интеграл вида

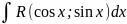
покажем что этот интеграл с помощью Подстановки tg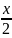 =t всегда сводится к интегралу от рациональной ф-ции. Выразим sinx и cosxчерез tg ,а след и через t sinx=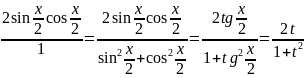

cosx=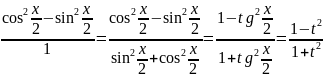

далее x=2arctg t , dx=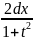

таким образом dx выразились рационально через t

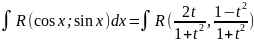
1.Если интеграл имеет вид 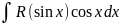,то подстановкаsinx=t,cosxdx=dt приводит этот интеграл к виду

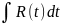
2.Если интеграл имеет вид 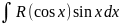то он приводится к интегралу от рациональной функции заменой cosx=t, sinxdx=-dt

3.Если подынтегральная ф-ция зависит только от tg x то замена tgx=t, x=arctgt , dx=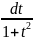 приводит этот интеграл к интегралу от рациональной ф-ции

4.Если подынтегральная ф-ция имеет вид ,но sin x и cos x входят только в четных степенях то применяется та же подстановка.

30)Определенный интеграл. Определение основные св-ва

Определение. Если существует   и он не зависит от

а) способа разбиения отрезка   на части и от

б) способа выбора средней точки,

то говорят, что   есть определенный интеграл от функции f(x) по отрезку [a, b].

         Функция f(x) называется в этом случае интегрируемой на отрезке [a, b]. Величины a и b называются нижним и верхним пределами интегрирования соответственно.

Свойства Если функция интегрируема на [a; b], то она интегрируема на любом отрезке 

Для любых a, b и c

Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.

Если f (x) – периодическая функция с периодом T, то для любого a

31) Интеграл как функция верхнего предела. Непрерывность. Формула Ньютона-Лейбница.

   Если функция y = f (x) интегрируема на отрезке [a, b], то, очевидно, она интегрируема также на произвольном отрезке [а, х], вложенном в [a, b]. Функция 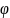(x)= ,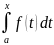

где х  [a, b], называется интегралом с переменным верхним пределом. Значение функции Ф (х) в точке х равно площади S(x) под кривой y = f (x) на отрезке [а, х]. В этом состоит геометрический смысл интеграла с переменным верхним пределом. Теорема. Если функция f (x) непрерывна на отрезке [a, b] то функция Ф (х) также непрерывна на [а, b]. Пусть Δх таково, что х + Δ х  [a, b]. Имеем что (x+∆x)= .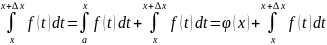

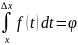По теореме о среднем найдется такое значение с  [ x, x + Δ x], что (x+∆x)= (x)+ (x)+f(c)* Δx.

Поскольку с  [x, x + Δ x], и функция f (x) ограничена, то переходя к пределу при Δ x → 0, получим 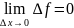, что и требовалось доказать.

Согласно формуле Барроу d/dx(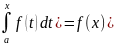 интеграл I(x) есть первообразная f(x). Пусть G(x) любая первооразная f(x), все первообразные отличающиеся на константу I=G(x)+C C= - G(a) I(x)=G(x)-G(a)

Сопоставляя это правило с определением определённого интеграла, получим формулу Ньютона—Лейбница 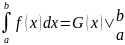=G(b) – G(a).

При применении формулы Ньютона-Лейбница несущественно, какой из пределов интегрирования больше: верхний или нижний.