1)Числовые ряды основные определения сходимость, критерий Коши. Понятие ряда тесно связано с понятием последовательности. Напомним основные результаты.

Последовательность – функция, определенная на множестве натуральных чисел . f(n),n €N

Последовательность называется сходящейся если она имеет конечный предел. Критерий коши: Последовательность Sn имеет конечный предел тогда и только тогда когда для любого эпселент больше нуля существует N такое что при любом n, m>N выполняется |Sn-Sm| < эпселента . Числовой ряд-это сумма членов числовой последовательности. Коши для ряда: Ряд An сходится тогда и только тогда когда для любого эпселент>0 существует N такое

что при n>N Выполняется |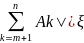

2)Положительные ряды признаки сравнения.

Ряд положительный если при всех n An>0.

Признак 1. Пусть есть две посл-ти 0<An<Bn для всех n .Тогда: 1)если ряд Bn сх-ся ,то сх-ся и ряд An 2)Если ряд An рас-ся то и ряд Bn рас-ся

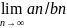Признак 2. Пусть есть две последовательность An>0 Bn>0 и существует =L L≠0 L≠∞ тогда ряды bn,an сх-ся или рас-ся одновременно 3)Признак Коши и признак Даламбера признак сходимости Коши пусть an> 0 существует 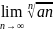=θ => 1)θ<1 то ряд an сх-ся 2)θ>1 то an рас-ся. 4)Признак сходимости Даламбера Пусть an>0 и существует предел 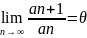тогда 1)при 0≤θ<1 сх-ся 2) при θ>1 рас-ся

4)Ряды с вещественными членами. Условная и абсолютная сходимость 1)Σan где an вещественные числа2) Σ|an| где все члены положительны Если ряд (2) сх-ся то ряд (1) абсолютно сходящийся.Из абсолютной сходимости следует обычная. Возможная ситуация 1) (2)сх-ся=>(1)сх-ся.2)(1)сх-ся =>(2)рас-ся условная сходимость (1).

5.Знакочередующиеся ряды Признак сходимости лейбница. 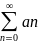an=(-1)ⁿ bn bn>0 Ряды удовлетворяющие таким свойствам называются знакочередующимися. Признак лейбница Пусть 1) bn убывает на[0;+∞) 2) bn→0 при n→0=>ряд сх-ся

6)Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция . Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно. Необходимое условие равномерной сходимости- . Критерий Коши равномерной сходимости: Критерий Коши для последовательности . Чтобы последовательность функций , определенных на множестве , равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого существовал номер , такой, что при всех больше либо равных одновременно для всех выполнялось неравенство

7) Теоремы о непрерывности: Последовательность непрерывных в точке функций сходится к функции непрерывной в этой точке. Последовательность функция непрерывна в точке , тогда непрерывна в .

Ряд непрерывных в точке функций сходится к функции непрерывной в этой точке.Ряд функция непрерывна в точке Тогда непрерывна в .

Теоремы об интегрировании: Теорема о переходе к пределу под знаком интеграла. функция непрерывна на отрезке , на , Тогда ,Теорема о почленном интегрировании. функция непрерывна на отрезке , на ,Тогда

Теоремы о дифференцировании. Теорема о дифференцировании под пределом. функция непрерывно дифференцируема на отрезке , сходится на отрезке ,Тогда — непрерывно дифференцируема на , на Теорема о почленном дифференцировании. функция непрерывно дифференцируема на отрезке , сходится

равномерно сходится на отрезке , Тогда — непрерывно дифференцируема на , на

8) Степенной ряд с одной переменной — это формальное алгебраическое выражение вида: в котором коэффициенты берутся из некоторого кольца . . Теорема Абеля: Пусть ряд сходится в точке . Тогда этот ряд сходится абсолютно в круге и равномерно по на любом компактном подмножестве этого круга.Обращая эту теорему, получаем, что если степенной ряд расходится при , он расходится при всех , таких что . Из первой теоремы Абеля также следует, что существует такой радиус круга (возможно, нулевой или бесконечный), что при ряд сходится абсолютно (и равномерно по на компактных подмножествах круга ), а при — расходится. Это значение называется радиусом сходимости ряда, а круг — кругом сходимости.

9) Область сходимости степенного ряда — круг вида , в котором ряд абсолютно сходится, а вне его, при , расходится. Иными словами, круг сходимости степенного ряда есть внутренность множества точек сходимости ряда. Радиус круга сходимости называется радиусом сходимости ряда. Круг сходимости может вырождаться в пустое множество, когда , и может совпадать со всей плоскостью переменного , когда . Радиус круга сходимости называется радиусом сходимости ряда.Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара: