Глава 1. Механические колебательные системы и их аналоги

З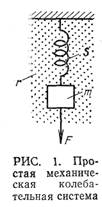 вук передается колебаниями частиц воздуха. Чтобы частицы воздуха могли совершить звуковые колебания, необходимо, чтобы они каким-то образом были приведены в колебательное состояние или, как принято говорить в акустике, были «возбуждены». Таким возбудителем или, иначе говоря, источником звука может быть, например, диффузор громкоговорителя, струна скрипки и т. п. Здесь колебания твердых тел (диффузор, струна) вызывают колебания частиц воздуха.

Твердое тело или совокупность нескольких твердых тел, участвующих в колебаниях, называется механической колебательной системой. Движение этих тел характеризуется либо перемещением х какой-нибудь точки тела, либо скоростью этой точки , либо ее ускорением .

Рассмотрим простую механическую колебательную систему (рис. 1), состоящую из массы m, укрепленной на пружине имеющей упругость s. Масса находится в вязкой среде, создающей сопротивление трения r. Если конец пружины оттянут из положения равновесия на расстояние х, то пружина стремится сократиться с некоторой силой. Очевидно, что эта сила тем больше, чем на большее расстояние оттянута пружина и чем больше ее упругость. Отсюда возвращающая сила пружины , стремящаяся вернуть оттянутый ее конец в положение равновесия, равна произведению xs, где х — расстояние, на которое оттянут конец пружины, а s — коэффициент упругости пружины.

В свою очередь s определяется как s = /x.

Отсюда единицей упругости называется упругость такой пружины, которая при растяжении на единицу длины (1 м) стремится сократиться с силой, равной также единице (1 Н)^*.

Свойства пружины можно характеризовать и величиной, обратной коэффициенту упругости. Эта величина называется коэффициентом гибкости и обозначается буквой c: c=1/s и соответственно c = x/ .

При перемещении тела возникают силы трения, тормозящие движение тела. При движении тела в вязкой среде значение силы трения F_r пропорционально скорости тела и коэффициенту r, характеризующему среду, в которой возникает трение, и называемому обычно сопротивлением трения. Следует заметить, что сопротивление трения может возникать не только при движении тела в вязкой среде, но и в результате внутреннего трения, например, трения частиц в толще материала пружины при ее растяжении или сжатии.

Сопротивление трения — одна из составляющих активного механического сопротивления. Характерной особенностью реальной механической системы (обладающей активным механическим сопротивлением) является то, что в ней всегда имеет место необратимый переход механической энергии в тепловую.

Сила трения может быть выражена как F_r=r или r=F_r/ .

Единицей активного сопротивления (трения) называется такое сопротивление, которое при перемещении тела со скоростью, равной единице (1 м/с), вызывает тормозящую силу, равную также единице (1 Н). Единица активного сопротивления измеряется в кГ/с (если учесть размерность силы кГ·м/с²).

Все тела стремятся сохранить состояние покоя или равномерного прямолинейного движения. Изменению этого состояния они сопротивляются с силой инерции, равной произведению массы на ускорение.

Пусть к телу с массой m (см. рис. 1) приложена сила F, направленная вниз. Под влиянием этой силы тело опустится на расстояние х от положения равновесия. При этом, кроме внешней силы F, на тело массой m действуют следующие силы: во-первых, сила инерции т , во-вторых, тормозящая сила трения, равная r , в-третьих, сила упругости пружины sx, которая стремится вернуть тело в положение равновесия. Процесс в такой механической системе подобен процессу в цепи переменного тока, состоящей из последовательного соединения индуктивности L, активного сопротивления R и емкости С.

Это подобие отражает тот факт, что в обеих системах имеет место превращение энергии из одного вида, в другой. Действительно, в механической системе кинетическая энергия движущегося тела превращается в потенциальную энергию растянутой пружины, и обратно. Часть энергии из-за наличия трения переходит в тепло. В электрической цепи энергия магнитного поля, появляющегося при прохождении электрического тока, превращается в энергию электрического поля (заряд конденсатора), и обратно. Часть энергии выделяется на активном сопротивлении в виде тепла. Поэтому масса, сопротивление трения и гибкость аналогичны соответственно индуктивности, активному сопротивлению и электрической емкости. Это подобие не является чисто внешним, формальным, а отображает физическое подобие рассматриваемых величин или, как их называют, параметров. Действительно, индуктивность в цепи препятствует как мгновенному возрастанию тока от нуля до какого-то конечного его значения при включении источника напряжения, так и спаданию тока до нуля сразу же при выключении напряжения. То же относится к массе в механической системе. Инертность тела препятствует мгновенному нарастанию скорости при приложении силы и не дает телу остановиться сразу.

Как уже отмечалось, часть энергии электрического тока благодаря наличию активного сопротивления превращается в тепло. Также превращается в тепло при наличии трения часть механической энергии. Чем больше гибкость пружины, тем большее смещение она получает при заданном значении силы. Чем больше электрическая емкость, тем больший заряд создается на конденсаторе при заданном приложенном напряжении. Заряд можно рассматривать как аналог смещения, а ток, следовательно, как аналог скорости. Аналогичны также электродвижущая сила и механическая сила, первая является причиной прохождения тока, вторая — движения тела.

Отсюда по аналогии колебательная скорость тела в простой колебательной системе, на которую действует сила F, меняющаяся по синусоидальному закону с круговой частотой, выражается следующим образом:

(1)

а ее модуль