Закон Гука.

Закона Гука описывается уравнением:

F_c = k · х.

Сила F_с деформирующая пружину колебательной системы прямо пропорциональна упругости (обратно пропорциональна гибкости) пружины и величине смещения х конца пружины. Рис.2

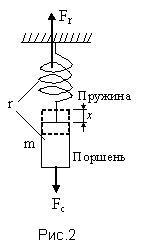
Сила растягивающая (сжимающая) пружину F_m (сила инерции массы m) в колебательной системе выражается формулой:

;

где x» - ускорение из 2-го закона Ньютона (F = ma), х - величина смещения поршня (или конца пружины) относительно состояния равновесия колебательной системы.

Трение r в колебательной системе создает силу F_r сопротивления противодействующую (направленную в противоположную сторону) силе F_c и растущую по мере растяжения или сжатия пружины. Пружина перестает растягиваться или сжиматься, когда растущая сила F_r становится равной силе F_c. Таким образом, трение обратно пропорционально скорости растяжения пружины:

.

Тогда сила трения F_r будет равна:

.

В электроакустических приборах возможно существование 2-х видов трения:

• вязкое трение возникает за счет противодействия колебаниям поршня (груза на конце пружины) вязкости воздуха,

• внутреннее трение возникает за счет трения частиц внутри материала пружины.

В соответствии с принципом Даламбера, согласно которому, сумма внешних сил, действующих на систему, находящуюся в равновесии, равна сумме сил противодействия (реакции), составим уравнение колебаний поршня:

;

то есть уравнение вынужденных колебаний будет иметь вид:

.

Если противодействующие силы отсутствуют, что означает F = 0, то в колебательной системе колебаний нет или происходят свободные колебания. Запишем уравнение:

Незатухающие (на практике почти незатухающие) свободные колебания (колебания с большим по сравнению с временем наблюдения временем затухания) возможны при малой величине трения r → min. В этом случае можно принять r = 0. Тогда и x′·r → min. То есть можно принять, что x′·r = 0. Тогда уравнение свободных колебаний можно переписать:

или , то есть ,

где, x» - ускорение смещения равно x» = ω²X, в уравнении свободных колебаний х достигает максимальных значений при х = Х. В этом случае можно записать:

, , .

Поскольку по определению , то

, то есть .

Запишем окончательно:

.

Так как математические преобразования проводились для режима отсутствия внешних вынуждающих воздействий и при силе трения равной 0 то можно окончательно записать уравнение для расчета частоты свободных колебаний ƒ₀ колебательной системы. Ее часто называют также резонансной частотой колебательной системы, то есть такой частотой, с которой будут колебаться элементы системы, если они вообще будут колебаться при отсутствии внешних воздействий:

.

Из уравнения частоты свободных колебаний видно, что частота свободных колебаний ƒ₀ зависит только от массы m и гибкости C_m системы.

Существует аналогия между механической колебательной системой, рассмотренной выше, и электрической колебательной системой (электрический колебательный контур).

В этих уравнениях масса m, трение r и гибкость C_m аналогичны соответственно индуктивности L, активному сопротивлению R, и емкости C_m. Смещение х в механической системе аналогично электрическому заряду Q, смещаемому в электрической цепи на расстояние х.

Масса m и индуктивность L. Масса m, обладая инерцией, препятствует всякому изменению скорости (или смещению). Аналогично индуктивность L препятствует всякому изменению электрического тока в цепи.

Гибкость C_m механической системы и электрическая емкость C. Гибкость C_m системы, это способность накапливать энергию. Аналогично и в электрической цепи конденсатор С накапливает электрическую энергию в виде электрического заряда Q.

Механическое сопротивление r и электрическое сопротивление R. В механической системе, r оказывает сопротивление, за счет чего теряется энергия, преобразуясь в тепло. Аналогично в электрической цепи R оказывает сопротивление электрическому току, за счет чего теряется энергия, преобразуясь в тепло.

Аналогия есть и для переменных величин: Смещение х аналогично смещению электрического заряда Q. Скорость смещения (колебательная скорость х′), аналогична величине тока I = Q′. Механическая сила F, причина всех перемещений в механической системе, возбуждающая механические колебания, аналогична электрическому напряжению U, так как напряжение (справедливо и для ЭДС) является причиной перемещения электрических зарядов Q.

Аналоги механических и электрических величин покажем в таблице:

Механические величины		Электрические величины
Масса m	кг	Индуктивность L	Гн
Смещение х	М	Активное сопротивление R	Ом
Трение r	кг/с	Электрическая емкость Cm	Ф
Гибкость Cm	м/Н	Электрический заряд Q	Кл
Скорость х′(v)	м/с	Электрический ток I	А
Механическая сила F	Н	Напряжение, ЭДС	В

Электромеханические аналоги величин позволяют использовать законы электротехники для расчетов механических колебаний акустических систем: микрофонов, телефонов, громкоговорителей, стабилизаторов скорости и других устройств.

Иофе В. К., Лизунков М. В. Бытовые акустические системы. — М.; Радио и связь, 1984.