Характеристики звуковой волны.
Период, длина волны, частота колебаний, угловая (круговая) частота, скорость звука.
Период колебаний Т (с) время, за которое совершается одно полное колебание.
Частота ƒ(Гц) колебаний, это количество колебаний (периодов Т), совершаемых за одну секунду.
Угловая частота 
(рад/с) (круговая частота, угловая
скорость, круговая скорость и др.)
Длина волны λ(м), это расстояние, пройденное звуковой волной распространяющейся в среде со скоростью С за время, равное одному периоду Т. (Рис. 5) Из определения следует:
(м).
Скорость звуковой волны или просто скорость звука, это скорость С (м/с) движения волны (сжатого или разреженного участка) в рассматриваемой среде. Для воздуха скорость звуковой волны равна С = 340 м/с.
Скорость звуковой волны С в газе можно выразить формулой:
,
Где γ = Ср/Сv- постоянная адиабаты – отношение теплоемкости среды при постоянном давлении Ср к теплоемкости среды при постоянном объеме Сv; Рас – атмосферное статическое давление; ρ – плотность среды (газа).
В твердых средах скорость звука определяется выражением
,
Где Е0 – модуль упругости Юнга, характеризует твердость среды; ρ – плотность среды.
Скорость звука по определению связана с длиной волны, периодом и частотой уравнениями:
(м/с).
Глава 4.
Звуковые волны.
Звуковое поле, это область среды, в которой распространяется звуковое колебание.
Основные характеристики звукового поля:
Смещение.
Скорость звука.
Колебательная скорость частиц среды, составляющих звуковое поле.
Давление звукового поля.
Удельное акустическое сопротивление звукового поля.
Интенсивность звука.
Акустическая мощность.
Плотность звуковой энергии.
Через любую точку звукового поля будут попеременно происходить сжатия и разряжения (растяжение) среды. Звуковая волна образуется перемещением областей сжатия (разряжения) среды в направлении от источника к приемнику.
Области сгущения и разряжения образуются за счет смещения частиц среды относительно своего стационарного положения на некоторую величину. Назовем ее смещение х (м). То есть каждая частица среды колеблется относительно своего стационарного положения и тянет за собой своих соседок. Те, в свою очередь, тянут своих соседок и т.д. Такая передача смещения соседкам происходит с некоторой скоростью, которую называют скоростью распространения звуковой волны или просто скоростью звука.
Если передается синусоидальное колебание, то смещение каждой частицы относительно стационарного (без звука) положения подчиняется синусоидальному закону. В этом случае колебание частиц происходит с некоторой частотой, то есть с некоторой колебательной скоростью V (м/с):
.
Назовем статическим давлением Рст атмосферное давление в любой точке среды содержащей звуковое поле при отсутствии звуковых колебаний.
Величину давления Рз, на которую изменяется статическое давление при наличии звуковых колебаний, назовем звуковым давлением.
Звуковое давление (Рз), это переменная величина полного давления (Рп), измеряется в единицах измерения Паскаль (1 Па = 1 Н/м2).
В любой точке звукового поля, в любой момент времени t, полное давление Рп будет равно сумме статического и звукового давлений Рз.
Покажем графически звуковое поле, в котором распространяются звуковые волны (Рис.7):
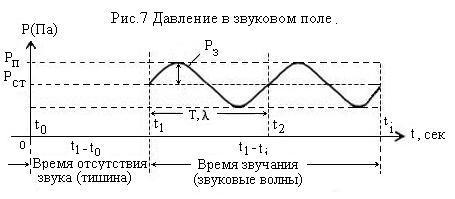
Интенсивность или иначе сила звука I определяется как поток звуковой энергии, проходящей через перпендикулярную звуковому лучу (направлению распространения) плоскую площадку единичной площади за единицу времени.
С практической точки зрения наиболее применима следующая формула: Интенсивность звука I, это часть акустической активной мощности W источника звука, проходящая через поверхность S фронта волны площадью в 1м2.
(Вт/м2).
Акустическая мощность понимается в данном случае как мощность создаваемая источником звука, проходящая через поверхность фронта волны содержащую точку, в которой измеряется акустическая мощность.
Относительно интенсивности периодических колебаний справедливо уравнение:
,
где I (Вт/м2) – интенсивность периодического колебания, Т (с) – период колебания, Рз (Н/м2) – звуковое давление, V (м/с) – колебательная скорость частиц среды.
Для непериодических колебаний справедливо уравнение:
.
Решением обоих интегральных уравнений будет уравнение:
,
где φ – угол между векторами давления и скорости.
Так как внутри среды существуют только продольные колебания, то векторы звукового давления и колебательной скорости будут параллельны. Значит угол между векторами звукового давления и колебательной скорости равен либо 0, либо 180 градусам, а косинус этих углов соответственно равен либо 1, либо -1. Тогда зависимость интенсивности от звукового давления и колебательной скорости принимает вид:
,
или
,
или
.
На границе среды векторы давления и скорости перпендикулярны, то есть продольные колебания превращаются в поперечные колебания границы среды (эффект сжатого ластика или хлебного шарика и других эластичных сред с явно выраженной границей, например сжатого воздушного шара). Угол между векторами колебательной скорости и звукового давления оказывается равным 90 или 270 градусам. Косинус этих углов равен нулю. Это значит, что, на границе среды звуковая энергия в направлении распространения (параллельно границе) не передается. через границу среды, параллельную направлению распространения звуковой волны, звуковая энергия не передается.
Естественно, в части среды близкой к ее границе, по мере приближения к ней происходит плавный поворот вектора колебательной скорости от 0 градусов до 90 градусов. В этой области среды происходит плавное угасание передаваемой в среде интенсивности (мощности в направлении параллельном границе среды) звуковой волны.
В соответствии с принципом электромеханической аналогии при наличии звукового давления (напряжения) и колебательной скорости (тока) должно существовать и сопротивление среды. Таким параметром в акустике является удельное акустическое сопротивление σ. Значит, по определению, удельное акустическое сопротивление равно:
.
Конечно удельное акустическое сопротивление величина комплексная, то есть удельное сопротивление содержит в себе как активную составляющую, так и реактивную определяемую упругими свойствами среды и ее подвижной массой.