21. Кинематика твердого тела. Углы Эйлера, угловая скорость.

Т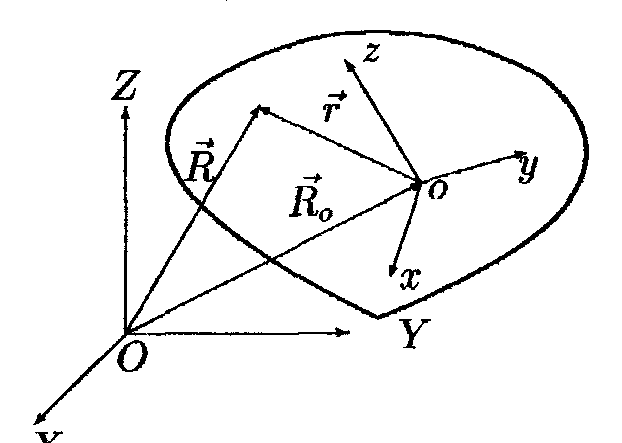 вердое тело в классической механике определяется как си­стема материальных точек, расстояние между которыми не изме­няется. Это может быть система из отдельных материальных то­чек, соединенных жесткими стержнями, или сплошное тело. По­ложение твердого тела относительно некоторой системы коорди­нат XYZ можно задать следующим образом (рис. 6.1). С твердым телом жестко связывается декартова система координат xyz, кото­рую в дальнейшем будем называть подвижной системой коорди­нат. Координаты начала подвижной системы координат задаются вектором . Ориентацию подвижной системы координат относи­тельно неподвижной системы координат обычно задают с помощью углов Эйлера. Для определения углов Эйлера совместим начала подвижной и неподвижной систем координат (рис. 6.2).

О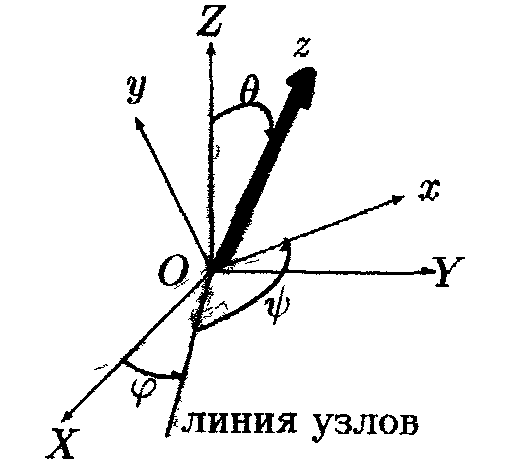 дин из углов Эйлера — это угол Θ между осями OZ и oz, от­считываемый от оси OZ. Линия пересечения плоскостей 'XOY и хоу называется линией узлов. Второй угол Эйлера φ — это угол между осью ОХ и линией узлов. Третий угол Эйлера φ отсчиты­вается в плоскости хоу от линии узлов до оси ох. Три угла Эйлера полностью определяют ориентацию подвижной системы координат относительно неподвижной. Задание трех координат подвижного начала координат и трех углов Эйлера полностью определяет по­ложение твердого тела. Поэтому твердое тело имеет шесть степе­ней свободы.

Координаты любой точки твердого тела можно задать как от­носительно неподвижной системы координат с помощью радиуса-вектора , так и с помощью радиуса-вектора , относительно по­движной системы координат (рис. 6.1). Из рис. 6.1 видно, что . (6.1)

Дифференцируя равенство (6.1) по времени, получим следующее выражение для скорости некоторой точки твердого тела: . (6.2)

Здесь — скорость подвижного начала координат. Так как век­тор проведен в твердом теле, то его длина остается постоянной и он испытывает только вращение. Направление оси вращения может быть различным в разные моменты времени. Направление оси вращения в данный момент времени зададим единичным век­тором , а угол поворота при вращении вокруг нее обозначим через Ф. Тогда, используя формулу для уравнения Лагранжа, используя определение обобщенного импульса , производную от запишем в виде

(6.3) Введем вектор мгновенной угловой скорости (6.4) Вектор угловой скорости направлен по оси вращения и связан с направлением вращения правилом правого буравчика, С учетом сделанных определений скорость произвольной точки твердого те­ла можно представить в виде суммы скорости подвижного начала координат и скорости, обусловленной вращением тела: (6.5)

Угловая скоростъ твердого тела не зависит от положения подвижиого начала координа. Перенесем начало подвижной систе­мы координат из точки о в точку о' вдоль вектора , как показано на рис. 6.3. Из рисунка и формулы (6.5) получим новое выражение для скорости:

, . (6.6)

Здесь — скорость нового начала подвижной с-мы координат, — координата точки тв. тела относительно новой подвиж­ной с-мы координат. Последнее равенство в (6.6) аналогично равенству в формуле (6.5) с той же самой угловой скоростью , что доказывает утверждение о независимости угловой скорости от выбора начала подвижной с-мы координат. Поэтому можно го­ворить об угловой скорости вращения тв. тела без указания где выбрано начало подвижной с-мы коорд.

Р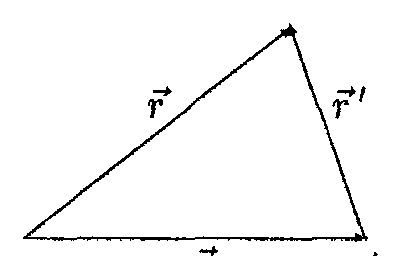 ис. 6.З Как и другие векторы, векторы угловой скорости можно скла­дывать. Запишем сумму трех угловых скоростей, каждая из кото­рых получается при изменении только одного из углов Эйлера. В результате получим , (6.7)

где векторы и — это единичные векторы, направленные соот­ветственно вдоль осей OZ и oz, вокруг которых происходит враще­ние при изменении углов φ и ψ. Единичный вектор направлен вдоль линии узлов, которая является осью вращения при изме­нении угла . Формула (6.7) дает разложение вектора угловой скорости по трем направлениям, которые не совпадают с напра­влениями координатных осей. Спроектируем векторы и на подвижные оси, что дает

, (6.8) . (6.9) Подставляя разложения (6.8) и (6.9) в формулу (6.7) и собирая коэффициенты при одинаковых базисных векторах, получим про­екции вектора угловойскорости наподвижные оси: , ,

. (6.10) -кинематическими формулами Эйле­ра. Они позволяют найти вектор угловой скорости, если задан за­кон изменения углов Эйлера как функция времени. Аналогичным образом после проектирования векторов и на неподвижные оси можно получить проекции вектора угловой скорости на непо­движные оси.