Теорема об изменении кинетического момента системы при ударе

При ударе изменение кинетического момента равно сумме моментов внешних ударных импульсов:.

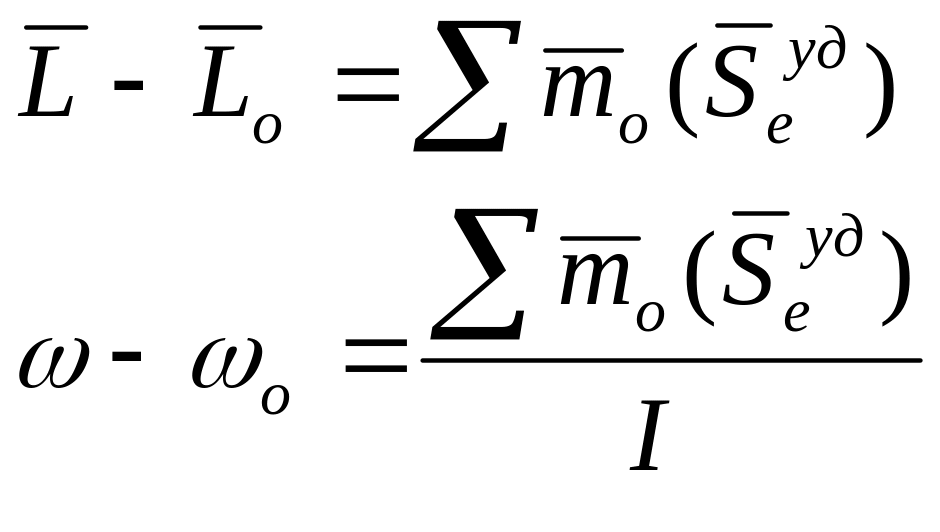т.к то

Т .е. изменение угловой скорости тела при вращение вокруг оси Z вследствие удара прямо пропорциональна моменту ударного импульса относительно оси и обратно пропорциональна моменту инерции тела относительно точки оси.

Центр удара

Если поменять местами оси привеса и качания, то период не изменится (теорема Гюйгенса). Точка К – центр удара. Если внешний удар приходится в точку К, то отсутствуют динамические составляющие реакции шарнира.

Примечание: для стержня длиной l центр удара приходится на h=2/3l

Приведённая длина физического маятника соответствует расстоянию от оси привеса до центра удара и определяется по формуле

Рекомендованные темы для самостоятельного изучения динамики системы; не вошедшую в учебную практику:

1. Движение тел, перемещение массы. Формула Циолковского.

Уравнение Мещерского.

2. Приближенная теория гироскопа. Навигационные системы.

3. Задачи оптимизации процессов и конструкций методом множителя Лагранжа.

4. Движение системы с n-степенями свободы. Элементы робототехники.

5. Электронные аналоговые машины.

^{В разработке электронной версии курса лекций по теоретической механике (динамика) принимали участие студенты групп: 03-А-АД 1- Брагин Д. И., 04-А-АД 2 - Филин А., 04-А-АД 3 -Ляшко В. Г.}

^{Рецензент: доктор технических наук, заведующий кафедрой теоретической механики, профессор Смелягин А. И}

^.

Краснодар, 2006 год