Обобщенные координаты. Число степеней свободы.
Независимые величины, заданием которых однозначно определяется местоположение любой точки системы, называются обобщенными координатами. Размерность их может быть различной.
Записывать эту величину будем q.
Число этих координат определяет число степеней свободы системы, в зависимости от чего в дальнейшем составляется определенное число дифференциальных уравнений, описывающих движение системы в обобщающих координатах.
Принцип виртуальных перемещений
Рассмотрим Mi
-точку
системы. Приложим к ней заданную силу
и реакцию связи (
),
тогда точка находится в равновесии:
δS
Дадим точке Мi
возможное
перемещение
допускаемое связью, и составим сумму
элементарных работ
на данном перемещении:
Т.к. связи идеальные, то второе слагаемое =0 и тогда:
Таким образом, сумма элементарных возможных работ всех заданных сил на любом возможном перемещении допускаемые связями в любой момент времени равна нулю.
В векторной форме
:
,
где
-элементарное
приращение радиус-вектора j
– той точки.
В координатной форме:
Золотое правило механики
Пусть на точку
действует движущая сила
,сила
сопротивления
.
Составим сумму элементарных работ этих
сил:
,
где
- элементарное возможное перемещение
точки приложения соответствующей силы.
Если отнести ко времени, то:
Но
,
тогда по модулю:
Т.е. силы обратно пропорциональны скоростям точек приложения:
Золотое правило механики:
«То, что теряется в силе – выигрывается в скорости»
Обобщенная сила Методы вычисления
Скалярная величина, соответствующая обобщенной выбранной координате qi (от 1 до s, где s – число степеней свободы) – есть отношение элементарной работы сил, действующих на систему на соответствующем возможном перемещении, вызванном приращением (вариацией) обобщенной координаты, к вариации обобщенной координаты δqj:
( k=1….n)
Т.к.
,
то найдем полный дифференциал при
фиксированном t:
Т.к. при фиксированном t правила дифференцирования совпадают с правилами варьирования, то:
Тогда обобщенная сила запишется:
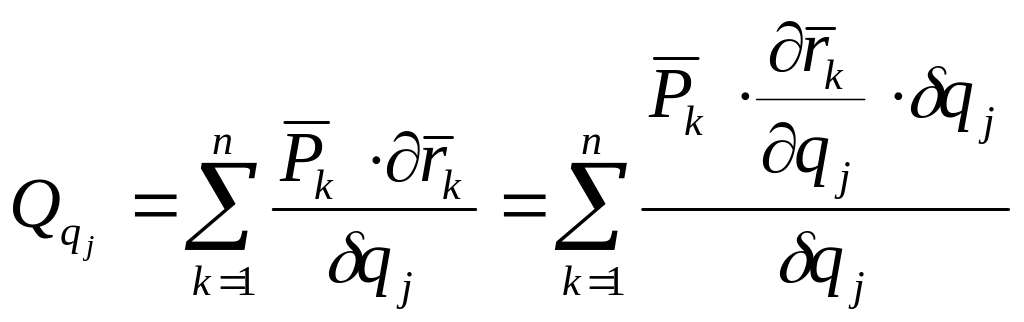
В аналитической форме:
Для сил, имеющих потенциал
Тогда выражение обобщенной силы будет иметь вид:
Дифференциальное уравнение движения механической системы в обобщенных координатах или уравнение Лагранжа 2-го рода
Полагаем, что
механическая система состоит из n-точек,
имеет S-степеней
свободы. Рассмотрим движение i-точки,
которое опишем радиус–вектором
,
который является функцией обобщенных
координат и времени:
Тогда скорость
i-точки
:
При условии
стационарных связей
.
Тогда, продифференцировав по
,
получим:
(1)
Уравнение (1) также называют тождеством Лагранжа.
Теперь рассмотрим кинетическую энергию системы. Она есть функция обобщенных координат, обобщенных скоростей и времени.
Для системы точек:
Вычисляем частное
производную по
по q
и по t:
Подставляя уравнения (1), получаем:
(2)
Возьмем полный дифференциал по t:
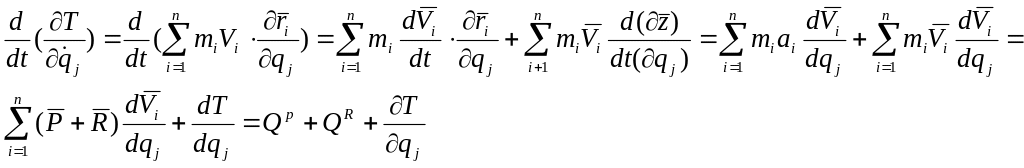
(3)
Уравнение (3) является дифференциальным уравнением системы в обобщенных координатах или уравнением Лагранжа 2 рода.
Количество этих уравнений зависит от числа степеней свободы s.
Алгоритм решения задач с применением уравнения Лагранжа 2 рода можно разбить на 6 пунктов:
1) выбрать обобщенную координату и определить число степеней свободы s;
2) вычислить кинетическую энергию системы через обобщенную координату;
3) записать уравнение Лагранжа 2 рода в соответствии с выбранной обобщенной координатой;
4) дифференцируем в соответствии с уравнением;
5) определяем обобщенную силу, соответствующую выбранной обобщенной координате. Для этого сначала надо определить потенциальную энергию системы или работу системы:
;
6) все найденные величины подставить в уравнение Лагранжа.