1.4.4. Пример.

□ Составляем систему уравнений Эйлера-Пуассона для

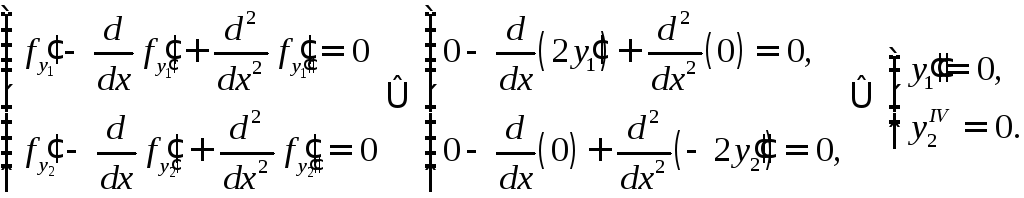
Общее решение:

.

Используем краевые условия:

Имеется единственная экстремаль . ■

1.5. Вариационная задача с подвижными границами.

В простейшей задаче в качестве краевых условий, определяющих класс допустимых функций, берется условие закрепления концов.

Рассмотрим два примера вариационных задач с подвижными границами, ограничившись функционалом, содержащим одну функцию и первую производную.

1. Задача с подвижными концами.

Это – задача заданные числа,.

Краевые условия не заданы, т.е. не заданы. С геометрической точки зрения такая задача состоит в определении кривой – графика функции, концы которого расположены на вертикальных прямыхи для которой соответствующее значение

функционала является экстремальным. Эту задачу называют задачей сподвижными концами.

Для допустимой вариации аргументаусловиетеперь не требуется, так что допустимыми вариациями аргумента являютсялюбые функции .

1.5.1. Теорема. (Необходимое условие экстремума в задаче с подвижными концами).

Если допустимая функция доставляет экстремум функционалу в задаче с подвижными концами, то эта функция удовлетворяет уравнению Эйлера, и, кроме того, так называемым естественным краевым условиям

.

□ Как и в теореме 1.4.1, для упрощения доказательства добавим условие: функция , доставляющая экстремум функционалу, дважды непрерывно дифференцируема:вместо(это используется при интегрировании по частям. Но теорема верна и без этого дополнительного условия).

Согласно теореме 1.2.11 вариация равна нулю при всех допустимых, в нашем случае – при всех, так что

(*теорема 1.3.1*).

Интегрируя по частям второе слагаемое, получаем

=. Значит,

.

Это равенство верно при любой функции , в частности для функции , у которой, и тем более для любой такой бесконечно дифференцируемой функции:

.

Но по лемме Лагранжа 1.1.2 на, т.е. функцияудовлетворяет уравнению Эйлера. Значит, остается равенство

,

справедливое при любой функции . В частности, оно верно для функции , у которой:

,

а также для функции , у которой:

. ■

Можно рассматривать и «смешанную» задачу, в которой один из концов закреплен, а другой конец свободно перемещается по вертикальной прямой. Например, (задано), а правый конец перемещается по прямой. Это дает естественное краевое условие

.

1.5.2. Пример (левый конец закреплен, правый подвижен).

□ Уравнение Эйлера: - линейное ДУ 2-го

порядка с постоянными коэффициентами с правой частью специального вида.

Его общее решение: . Из краевого условиянаходим. На правом конце естественное краевое условие имеет вид

Имеется единственная экстремаль .■

2. Задача с подвижными границами.

Рассмотрим функционал , определенный

на непрерывно дифференцируемых функциях , у которых концы графиков лежат на кривыхи(и- тоже непрерывно дифференцируемые функции).

Например, если функция такова, что , то для нее функционал вычисляется по формуле

, а если , то по формуле. Имеется в виду, что каждая допустимая функция непрерывна на своем отрезке, содержащемся в отрезке. Таким образом, пределы интеграла меняются от функции к функции.

Требуется найти экстремум такого функционала. Соответствующую теорему сформулируем без доказательства (доказательство сложное).

1.5.3. Теорема (Необходимое условие экстремума в задаче с подвижными границами).

Если допустимая функция доставляет экстремум функционалу

(1)

при краевых условиях , то эта функцияявляется экстремалью функционала (1) (т.е. удовлетворяет уравнению Эйлера для его интегранта) и удовлетворяетусловиям трансверсальности

(2)

(Эти условия учитывают то, что концы кривой лежат на заданных кривыхи).

Таким образом, для решения этой задачи нужно:

1. Найти общее решение уравнения Эйлера (оно 2-го порядка, поэтому две произвольные постоянныеи).

2. Из краевых условий и из условий трансверсальности (2) определить постоянные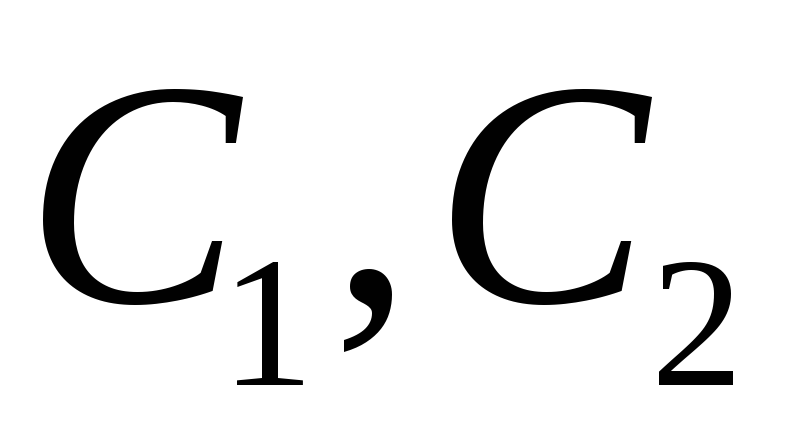и неизвестные концы.

3. Вычислить экстремум функционала (если есть уверенность, что найденная функция действительно дает экстремум).

Можно рассматривать и «смешанную» задачу, в которой один из концов закреплен или перемещается по вертикали, а второй конец перемещается по графику какой-либо функции .

1.5.4. Пример. Найти кратчайшее расстояние между кривыми и.

□ Задача состоит в нахождении минимума функционала (длина кривой ) при краевых условиях, где.

Составим уравнение Эйлера: Его общее решение (прямая). Для нахожденияиспользуем краевые условия:,

и условия трансверсальности:

Из системы уравнений

находим .

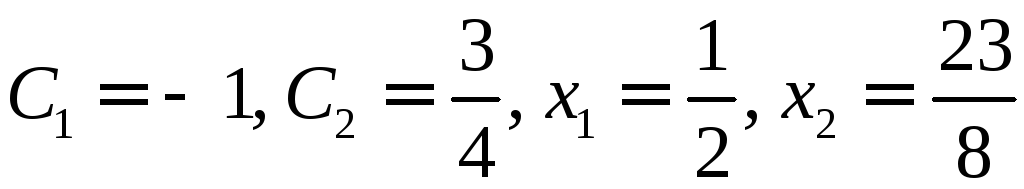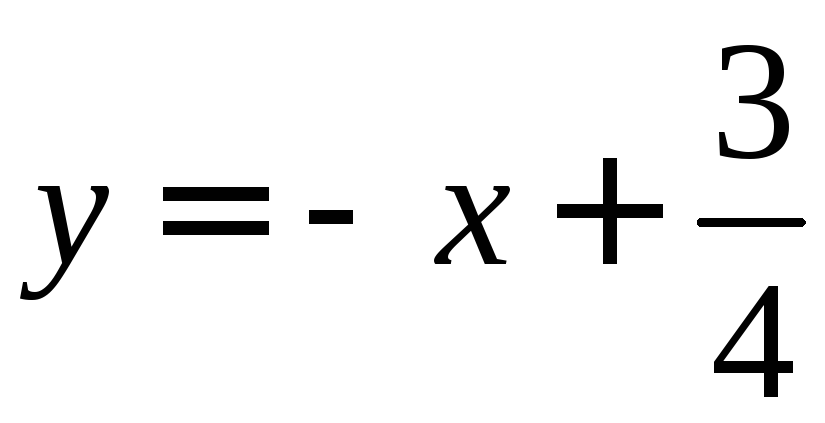Экстремаль:. Она единственная, а по смыслу задачи минимум имеется. Значит функцияи доставляет экстремум функционалу. Найдем минимальное расстояние:

. ■
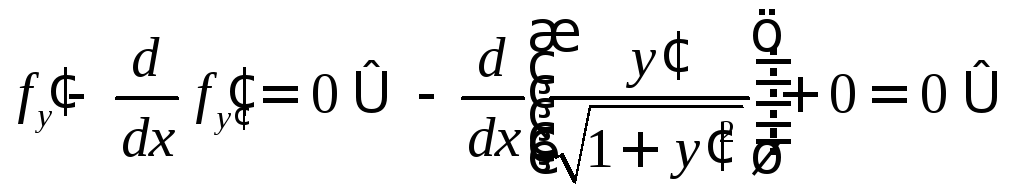