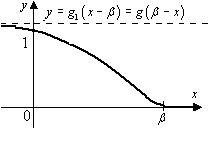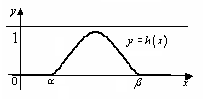Уфимский государственный авиационный технический университет

ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

И ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Учебное пособие

Уфа 2003

I. Элементы вариационного исчисления

1.1. Введение и вспомогательные утверждения

Вспомним понятие экстремума числовой функции числового аргумента :

Точка – точка локального максимума (минимума), а значение локальный максимум (минимум), если для всех точек,

достаточно близких к , выполняется неравенство, т.е. существует окрестность, такая, что.

При этом, если существует производная , то(необходимое условие локального экстремума). Если, то наличие или отсутствие локального экстремума проверяется с помощью достаточного признака локального экстремума.

В вариационном исчислении решают задачи на экстремум числовых функций функционального аргумента: у таких функций значениями функций тоже являются числа, но значениями аргумента является не числа, а функции. В отличие от функций векторного аргумента такие функции называют функционалами.

Пример. Среди всех гладких кривых, соединяющих точки

и , найти ту, длина которой наименьшая (решение очевидное:). Формализуем задачу. Обозначиммножество всевозможных функций, непрерывно дифференцируемых на, т.е. гладких функций.

Нужно среди функций , принимающих заданные значения, найти ту, для которой длина графика

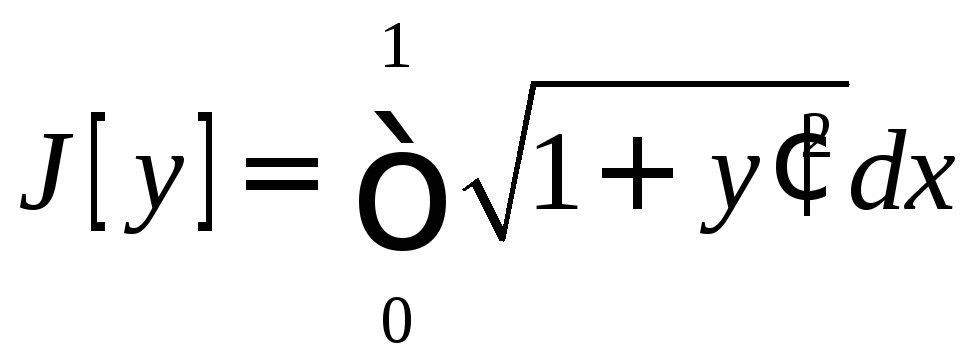(1)

наименьшая.

Формула (1) каждой функции ставит в соответствие определенное числодлину кривой, так что имеем отображение. Это и есть пример функционала. Аргументом функционала является гладкая кривая, а значением функции – число. При значении аргументафункционалимеет минимум, равный.

Ввиду удобства геометрического языка аргумент функционаланазывают «точкой», так что функционалв примере имеет минимум в точке.

Для характеристики близости точек (т.е. близости функций) вводят понятия расстояния между функциями, окрестности точки (т.е. окрестности функции). Это позволяет рассматривать вопрос об экстремуме функционала.

Рассмотрим некоторые утверждения, используемые в дальнейшем.

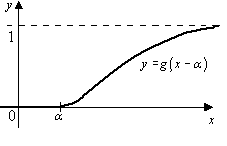
1.1.1. Пример.

Построим бесконечно дифференцируемую функцию, положительную на заданном интервале и равную нулю вне этого интервала.

□ Покажем сначала, что функция 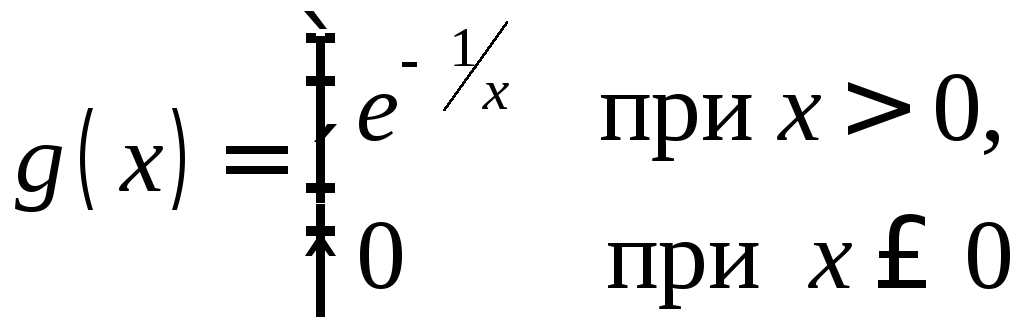бесконечно дифференцируема (т.е. имеет производные любого порядка) на. В точкахэто очевидно: если, то, если, томожно найти по правилам дифференцирования. Приимеем

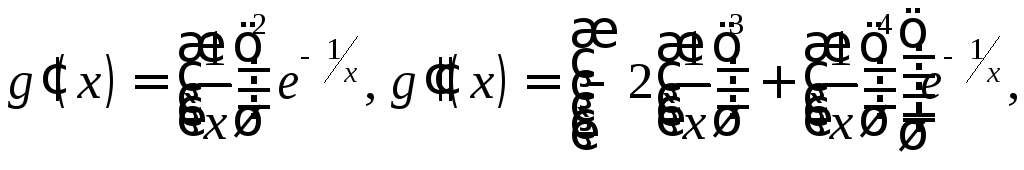
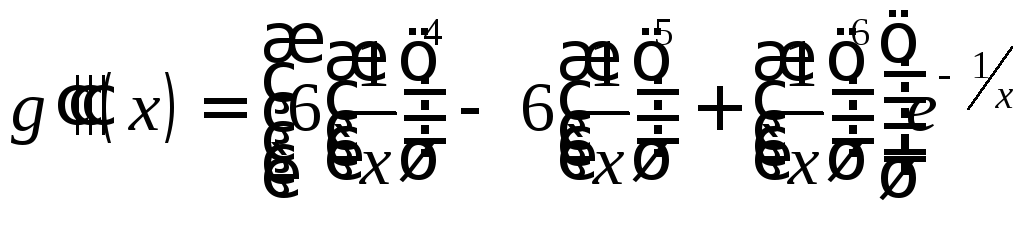
и т.д. Заметим, что производная любого порядка имеет вид

,

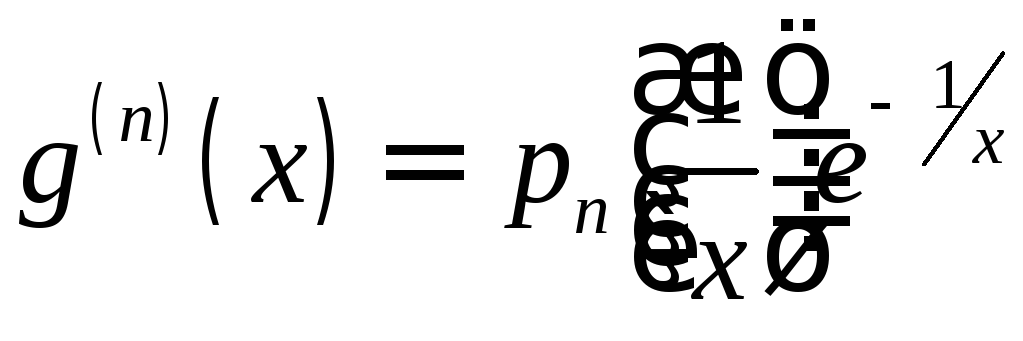где 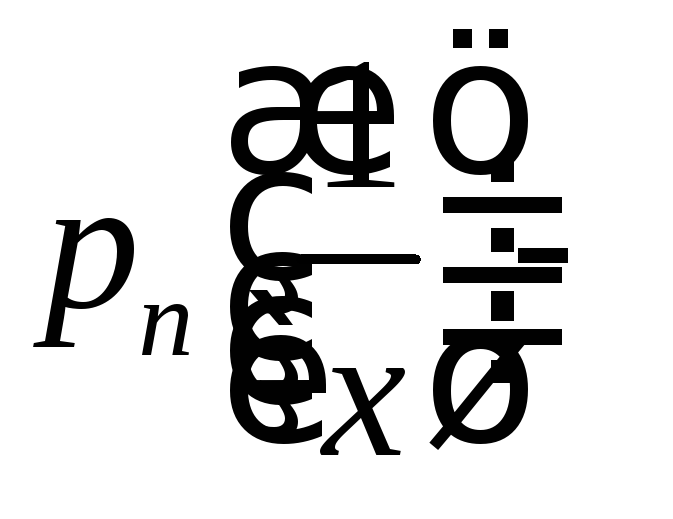некоторый многочлен от

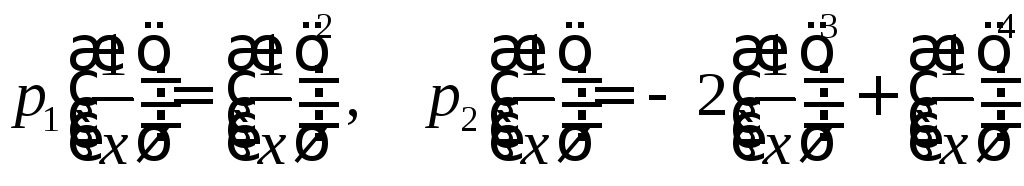и т.д.

В точке производные придется вычислять по определению производной:

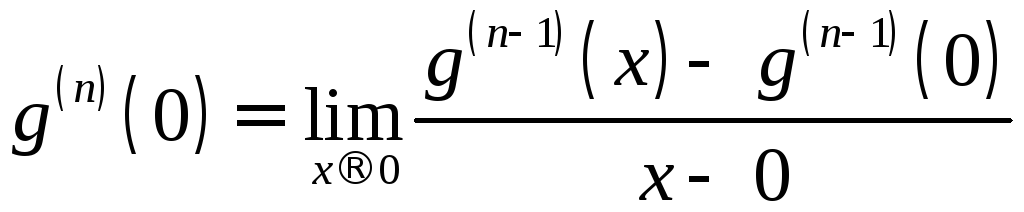
(если пределы при слева и справа существуют и совпадают, то их общее значение и будет).

Ищем

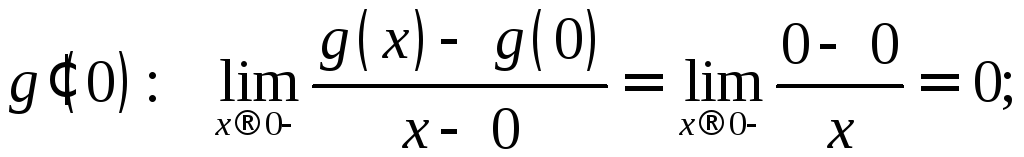
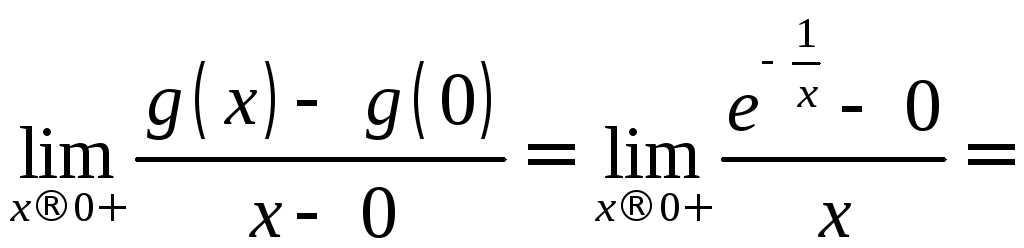
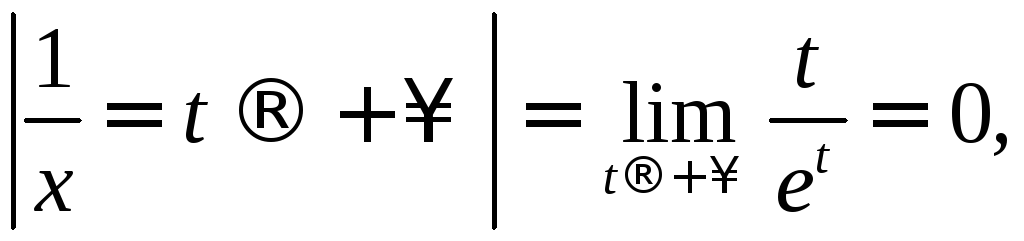так как экспонента растет быстрее . Нашли.

Ищем

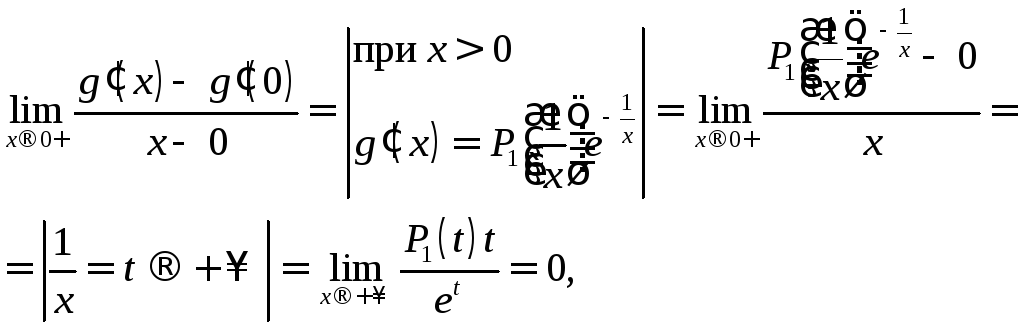
так как экспонента растет быстрее любого многочлена. Нашли .

Так можно найти при любом: если найдено, что, то

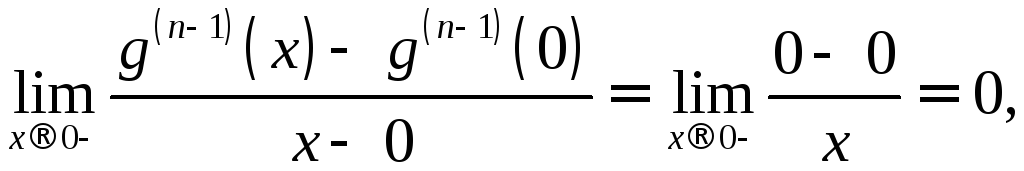
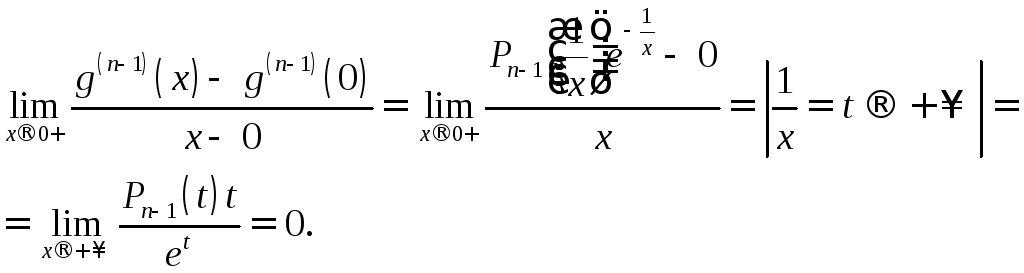
Нашли .

Итак, бесконечно дифференцируема во всех точках интервала.

Функции тоже бесконечно дифференцируемы во всех точкахкак сложные функции, составленные из бесконечно дифференцируемых звеньев (например,состоит из бесконечно дифференцируемых функций(как было показано) и). Поэтому произведение бесконечно дифференцируемых функций

бесконечно дифференцируема на . Это и есть искомая функция. Она положительна на интервале, так как

и равна нулю при .