- •Учебное пособие
- •I. Элементы вариационного исчисления
- •1.1. Введение и вспомогательные утверждения
- •1.1.1. Пример.
- •1.1.2. Лемма Лагранжа
- •1.2. Основные понятия
- •Число обладает свойствами:
- •Величина, определенная равенством , является нормой.
- •1.2.5. Замечание.
- •1.3. Вычисление вариации интегрального функционала.
- •1.4. Простейшая вариационная задача
- •Если функционал от вектор - функции
- •1.4.3. Пример.
- •1.4.4. Пример.
- •1.5. Вариационная задача с подвижными границами.
- •1.6. Вариационные задачи на условный экстремум
- •Пусть требуется найти экстремум функционала
- •1.6.3. Пример
- •1.6.6. Пример.
- •II. Элементы оптимального управления
- •2.1. Постановка задачи оптимального управления
- •2.2. Линейная стационарная задача
- •2.2.2. Определение.
- •2.2.3. Определение.
- •2.3. Примеры синтеза оптимального управления
- •Составим сопряженную систему
- •2.3.1. Пример
- •2.3.2. Пример.
- •Сопряженная система
- •2.3.3. Пример.
- •III. Примеры решения задач.
- •3.1. Простейшие задачи вариационного исчисления
- •3.2. Задачи для самостоятельного решения
- •3.3. Варианты заданий: «Простейшие задачи вариационного
- •3.4. Задачи с подвижными границами
- •Задача 1.
- •Условие трансверсальности
- •3.5. Варианты заданий: «Задачи с подвижными границами»
- •3.6. Варианты заданий: «Задачи по оптимальному управлению»
Величина, определенная равенством , является нормой.
□ Проверим свойства нормы (1.2.1).
Очевидно, что
 ,
так что
,
так что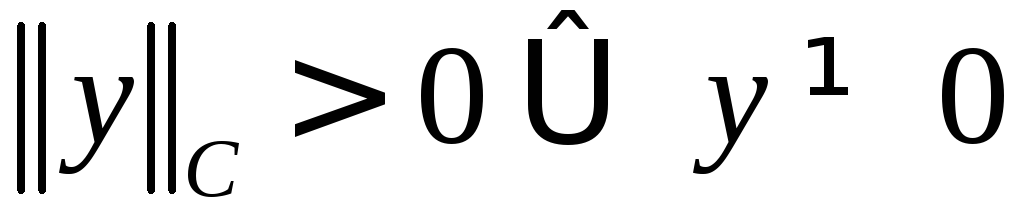 .
Очевидно также, что
.
Очевидно также, что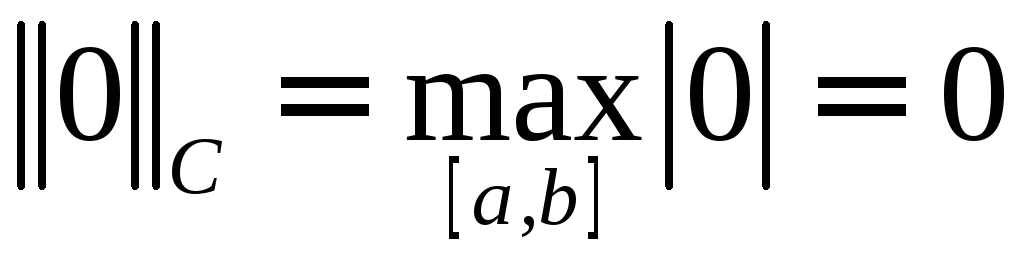 .
.При
 равенство
равенство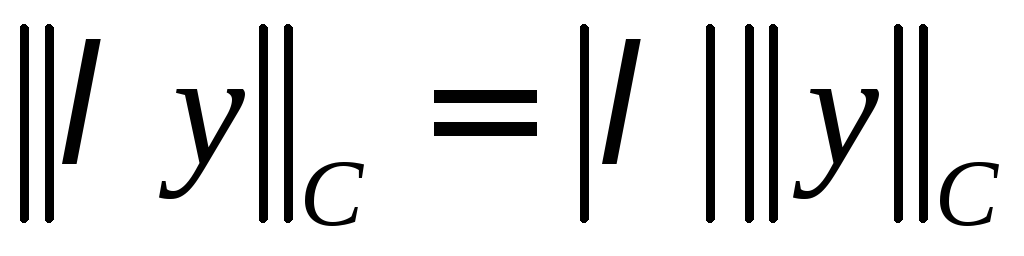 очевидно, так как
очевидно, так как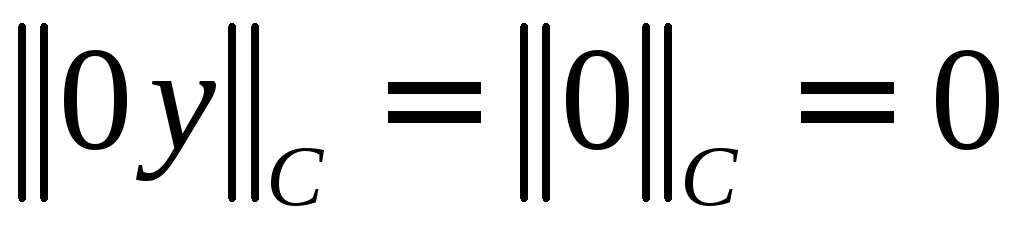 и
и
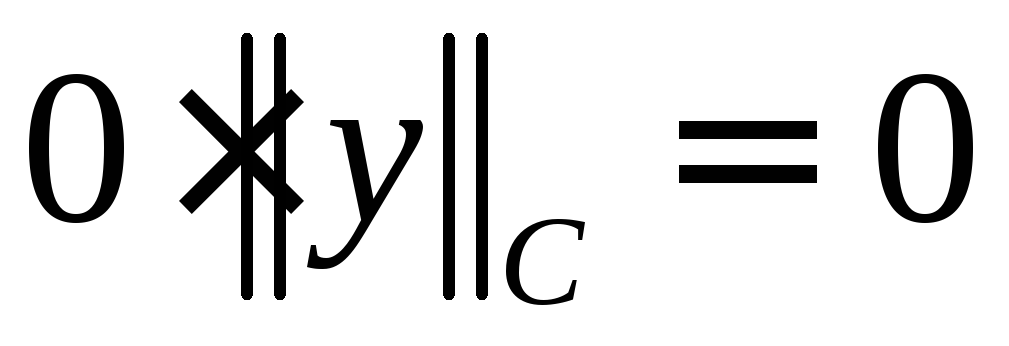 .
Пусть
.
Пусть .
Тогда
.
Тогда
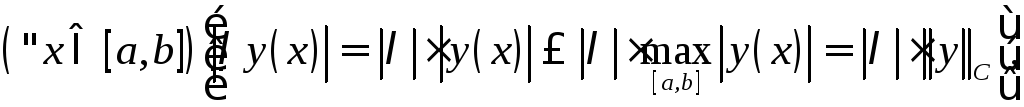
и,
в частности,
![]() ,
т.е.
,
т.е.![]() .
(1)
.
(1)
Обратно,
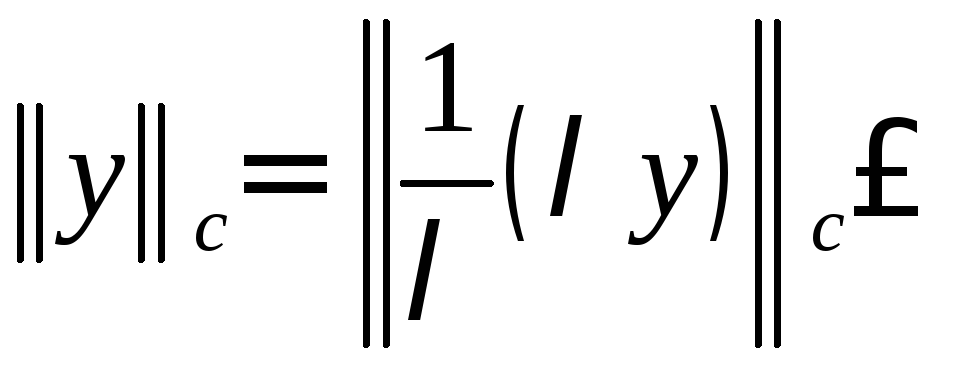
![]() по доказанному, для
по доказанному, для![]()
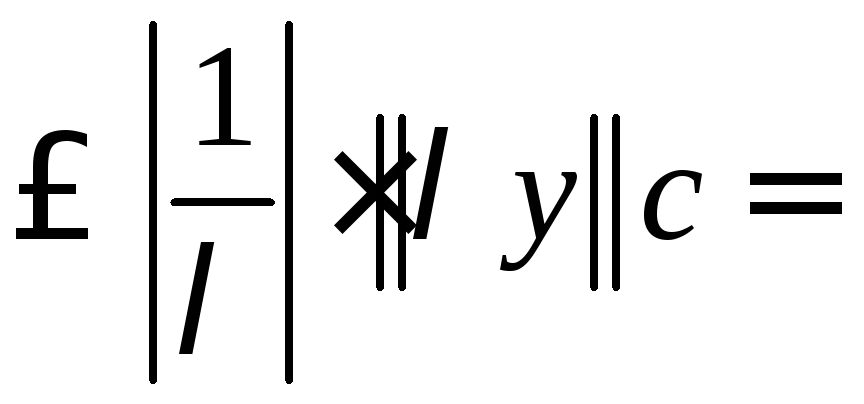
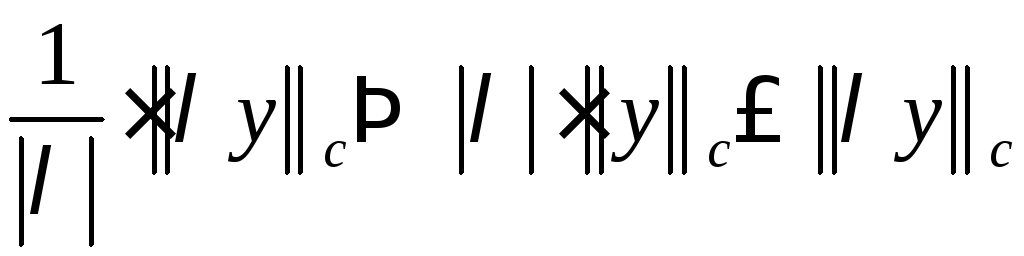 .
(2)
.
(2)
Из
неравенств (1) и (2) получаем
![]() .
.
3)
![]()
![]()
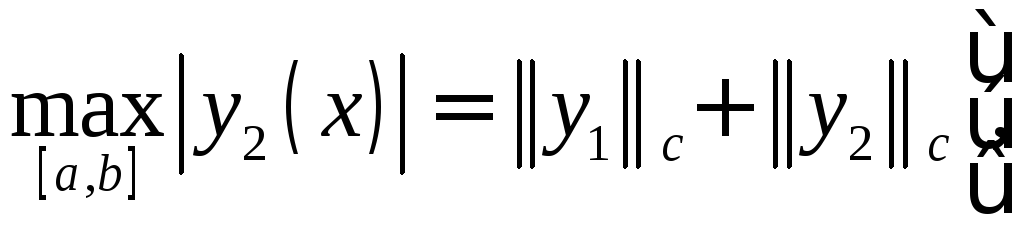 и,
в частности,
и,
в частности,
![]() ,
т.е.
,
т.е.![]() .■
.■
Таким
образом, пространство
![]() с нормой
с нормой![]() является нормированным пространством.
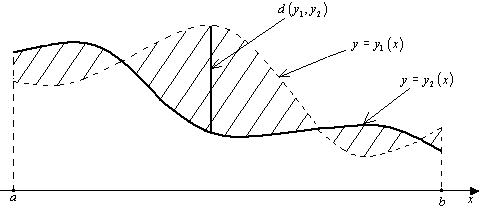
Расстоянием между точками
является нормированным пространством.
Расстоянием между точками![]() и
и![]() этого пространства является число
этого пространства является число
![]() – максимальное расстояние по вертикали
между графиками функций
– максимальное расстояние по вертикали
между графиками функций![]() и
и![]() .
.
|
|
Элементы
пространства
![]() непрерывно дифференцируемые, т.е.гладкие
функции. Функция
непрерывно дифференцируемые, т.е.гладкие
функции. Функция
![]() в каждой точке
в каждой точке![]() имеет невертикальную касательную с
угловым коэффициентом
имеет невертикальную касательную с
угловым коэффициентом![]() ,
которая ввиду непрерывности
,
которая ввиду непрерывности![]() непрерывно (без скачков) меняет свое
положение при движении вдоль графика
непрерывно (без скачков) меняет свое
положение при движении вдоль графика![]() .
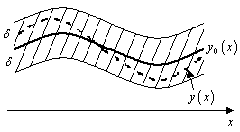
Поэтому элементы
.
Поэтому элементы![]() этого пространства естественно считать
близкими, если не только мало расстояние
по вертикали между их графиками, но еще
мало отличаются их касательные на всем
этого пространства естественно считать
близкими, если не только мало расстояние
по вертикали между их графиками, но еще
мало отличаются их касательные на всем![]() ,
т.е. разность
,
т.е. разность![]() мала. Поэтому расстоянием
мала. Поэтому расстоянием![]() следует считать число
следует считать число
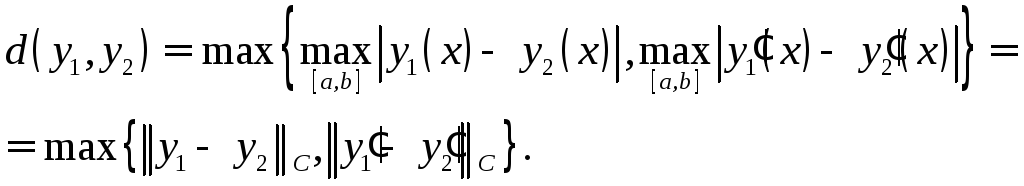
(![]() тоже существует, т.к. функция
тоже существует, т.к. функция![]() непрерывна на отрезке
непрерывна на отрезке
![]() ).
Следовательно, нормой элемента
).
Следовательно, нормой элемента![]() (т.е. расстоянием до
(т.е. расстоянием до![]() )
следует считать число
)
следует считать число![]() .
Вообще,
.
Вообще,![]() .
.
1.2.5. Замечание.
Очевидно,
что
![]() .
.
1.2.6.
Теорема
(о норме
![]() )
)
Величина,
определенная равенством
![]() ,
является нормой.
,
является нормой.
□ Докажем
для
![]() (для
(для![]() доказательство аналогично).
доказательство аналогично).
Проверим
свойства нормы (1.2.1) учитывая, что для
![]() они проверены.
они проверены.
Пусть
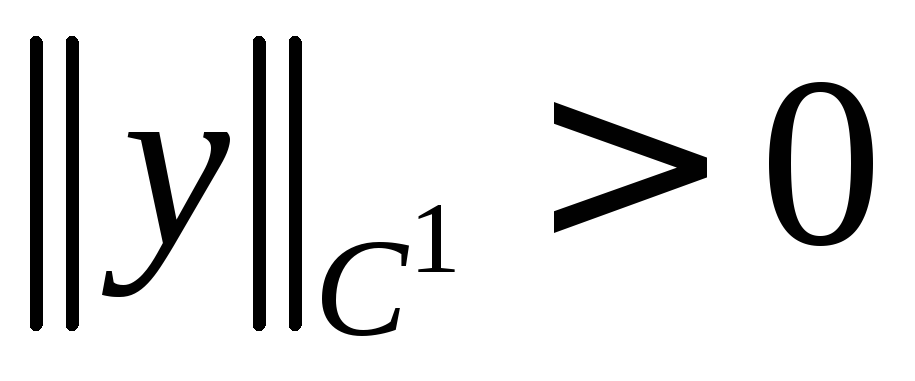 ,
т.е.
,
т.е.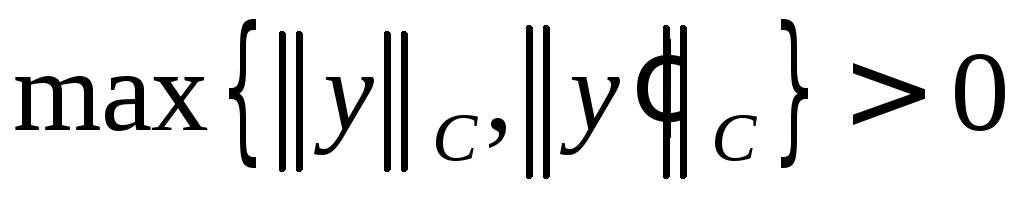 .
Тогда хотя бы одно из чисел
.
Тогда хотя бы одно из чисел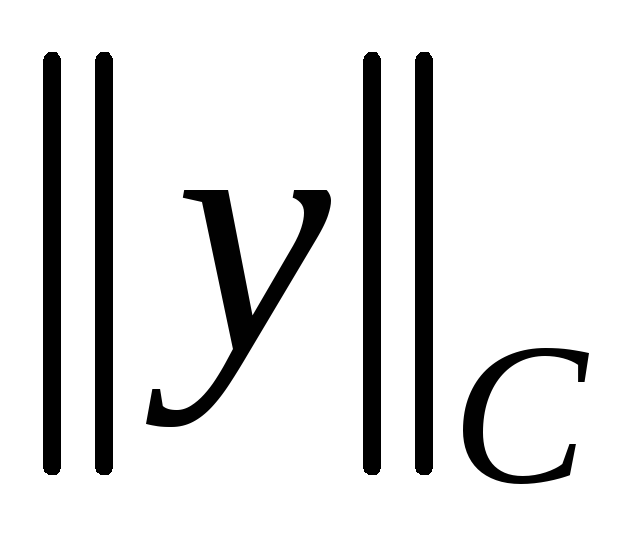 и
и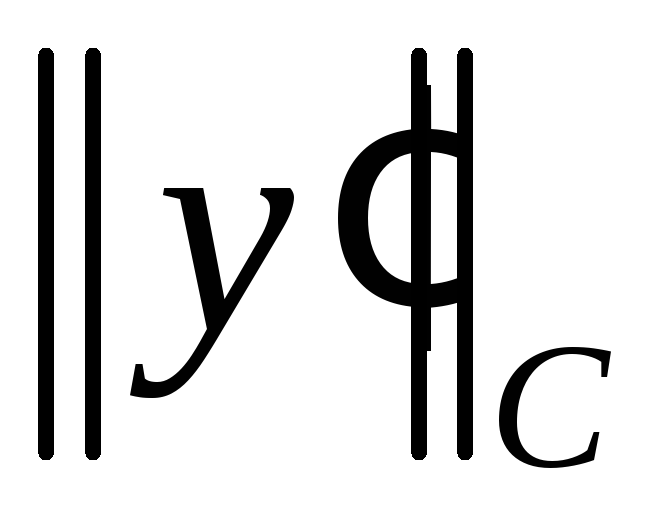 больше нуля. Если
больше нуля. Если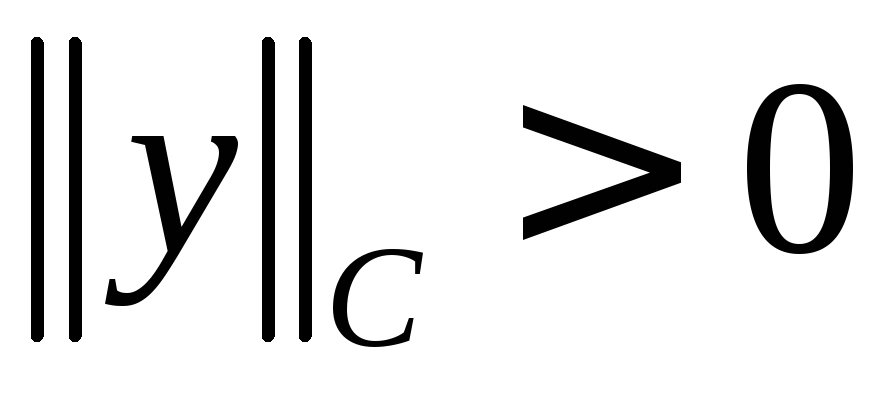 ,
то по теореме 1.2.4 (1)
,
то по теореме 1.2.4 (1) .
Если
.
Если ,
то по той же теореме
,
то по той же теореме ,
т.е.
,
т.е. .
Таким образом, в любом случае
.
Таким образом, в любом случае .
.
Пусть
обратно,
![]() .
Тогда по теореме 1.2.4 (1)
.
Тогда по теореме 1.2.4 (1)![]() ,
значит,
,
значит,![]()
![]() .
.
Доказано,
что
![]() .
Далее
.
Далее![]() очевидно.
очевидно.
При
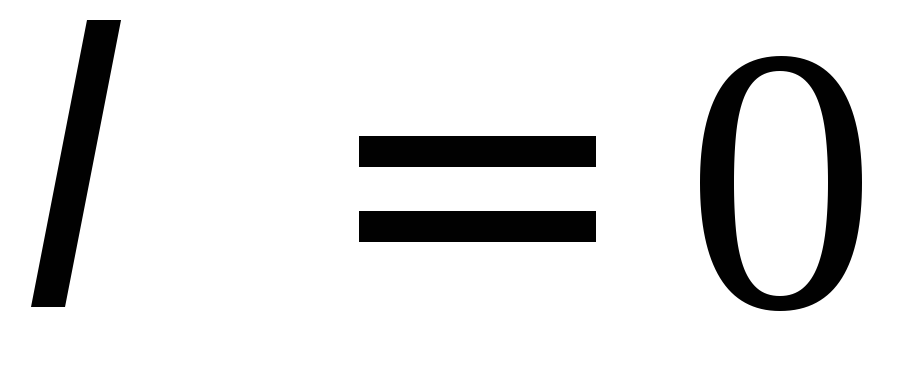 равенство
равенство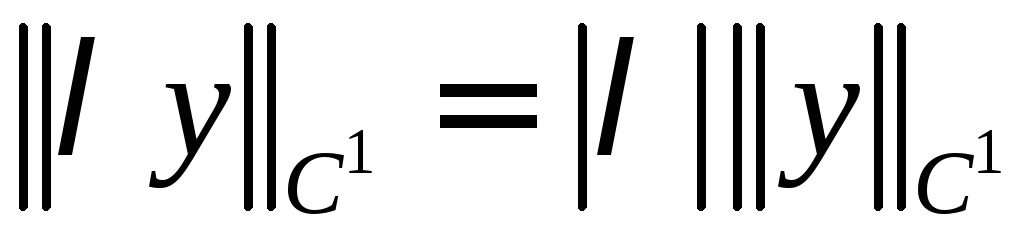 очевидно:
очевидно: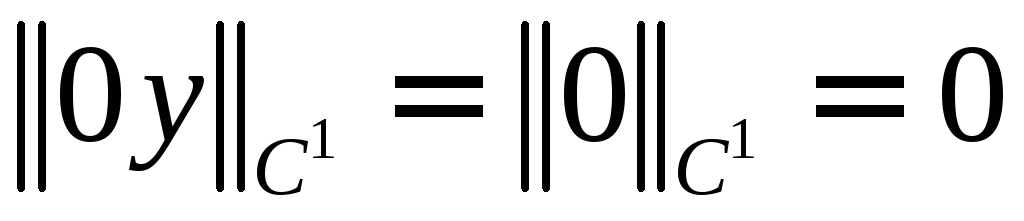 и
и
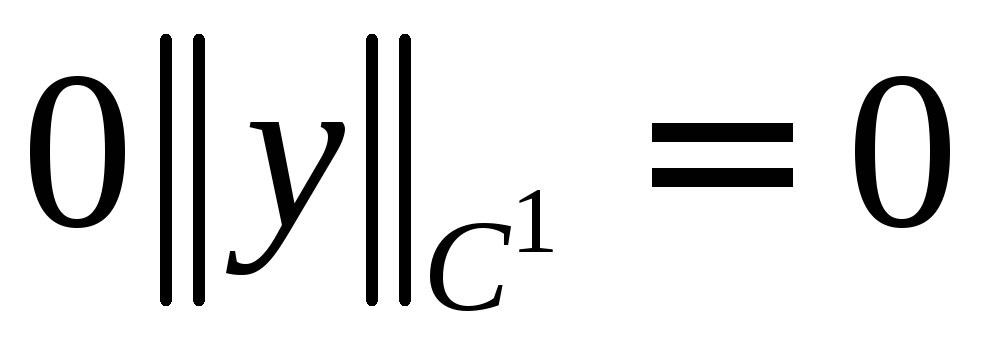 .
Пусть
.
Пусть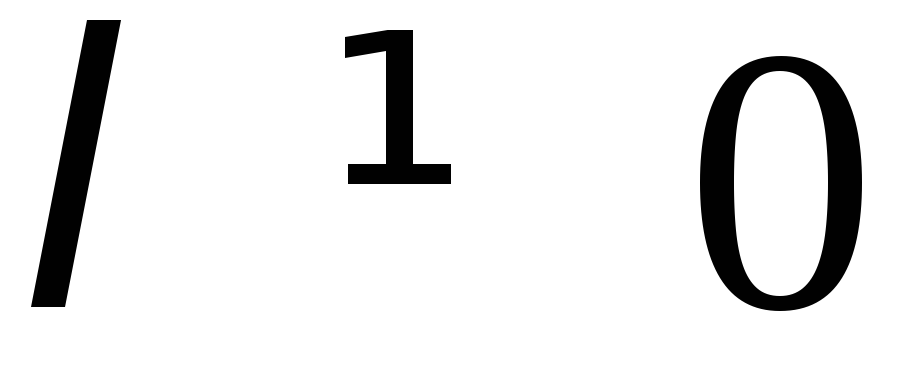 .
Тогдато по
теореме 1.2.4
(2)
.
Тогдато по
теореме 1.2.4
(2)
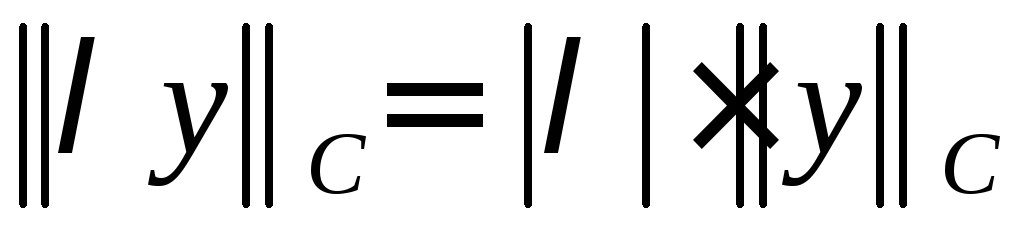 ,
,
 ,
а согласно замечанию1.2.5
,
а согласно замечанию1.2.5
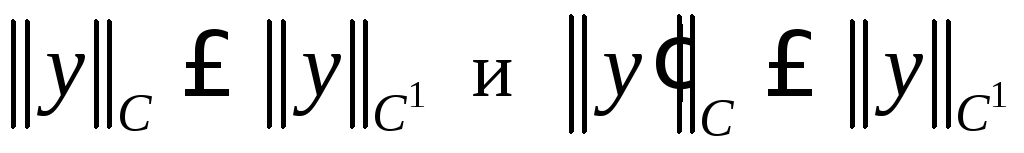 .
Поэтому
.
Поэтому
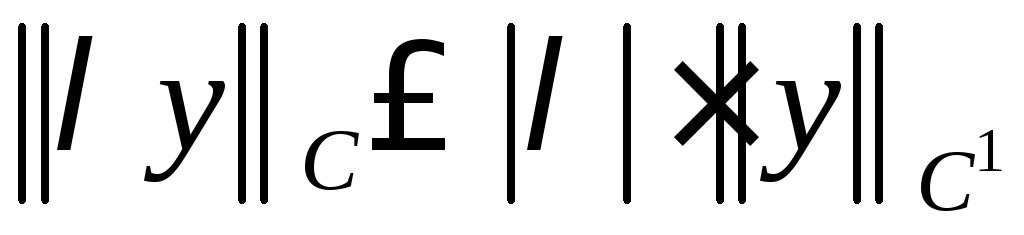 и
и
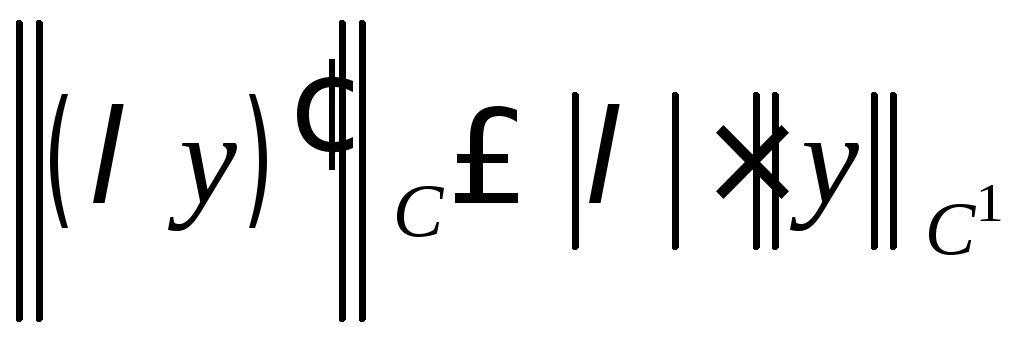 .
Значит, и
.
Значит, и
 ,
т.е.
,
т.е.
![]() .
(3)
.
(3)
Обратно,
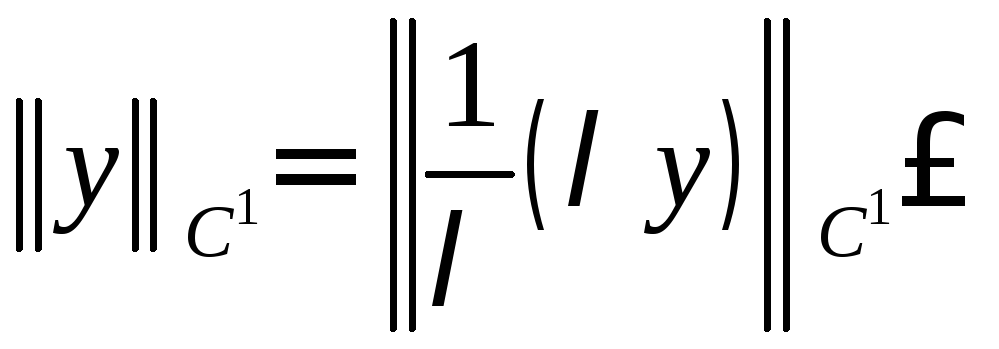
![]() по доказанному для
по доказанному для![]()
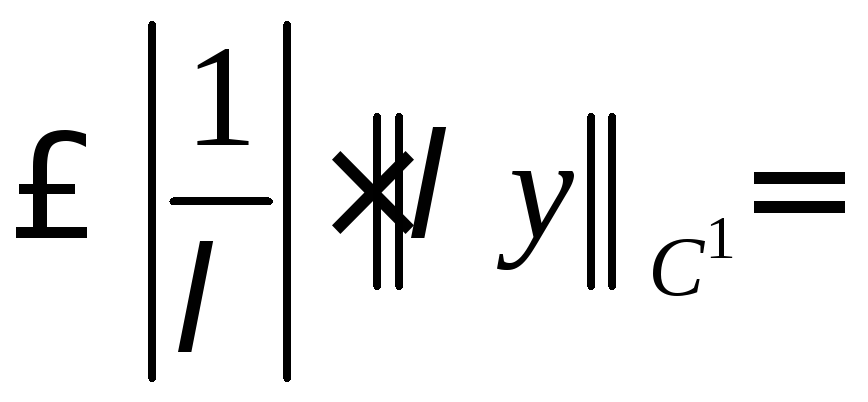
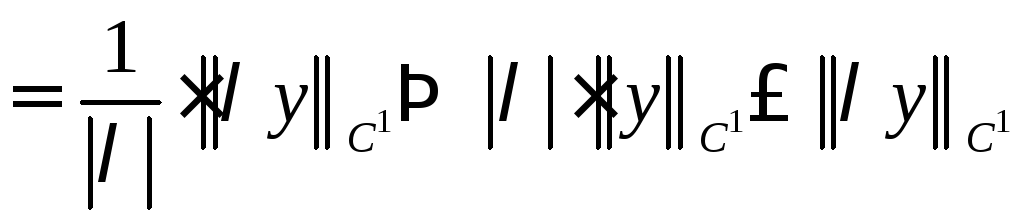 .
(4)
.
(4)
Из
неравенств (3) и (4) получаем
![]() .
.
По теореме 1.2.4 (3)
 ,
,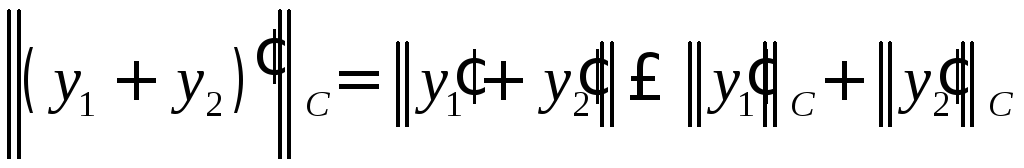 ,
а согласно замечанию 1.2.5
,
а согласно замечанию 1.2.5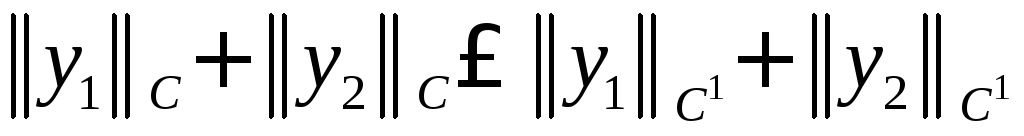 и
и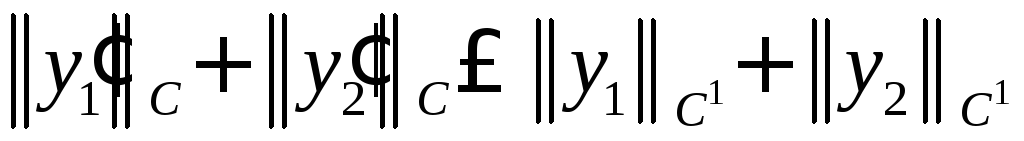 .
Поэтому
.
Поэтому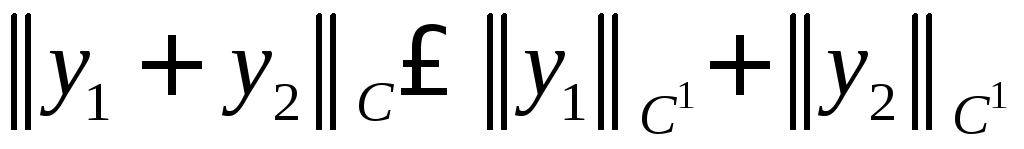 и
и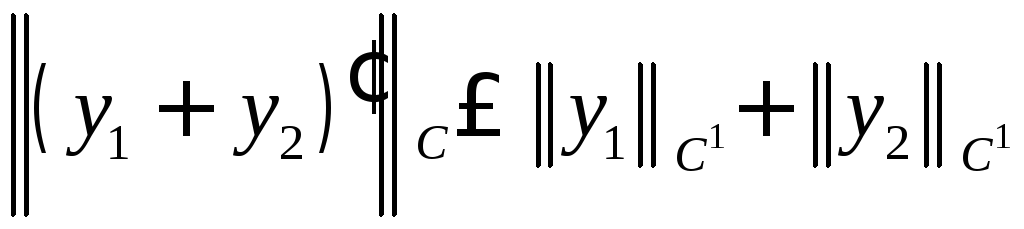 ,
значит,
,
значит,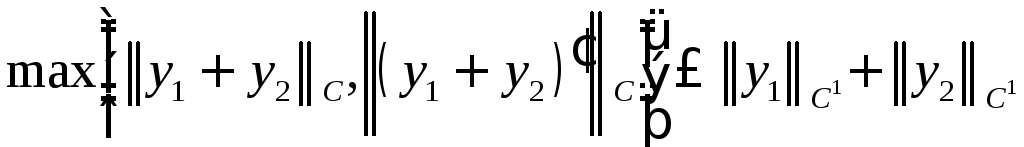 ,
т.е.
,
т.е.
![]() .
■
.
■
Таким
образом, пространство
![]() с нормой
с нормой![]() является нормированным пространством.
является нормированным пространством.
Расстоянием
между точками
![]() является число
является число
![]() .
.
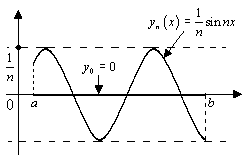
Замечание.
Функции,
близкие по норме пространства
![]() ,
могут сильно отличаться по норме
пространства
,
могут сильно отличаться по норме
пространства
![]() .
Например, функции
.
Например, функции![]() и
и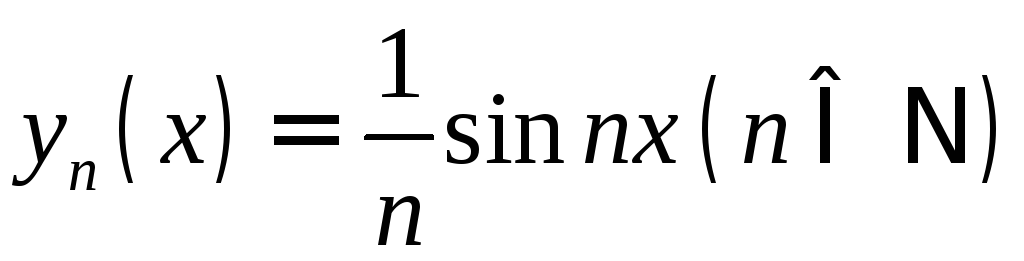 обе принадлежат
обе принадлежат
|
|
и
пространству
|
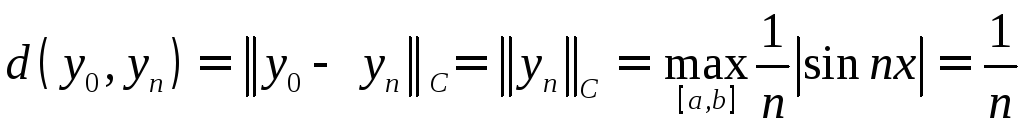 .
По норме
.
По норме
![]()
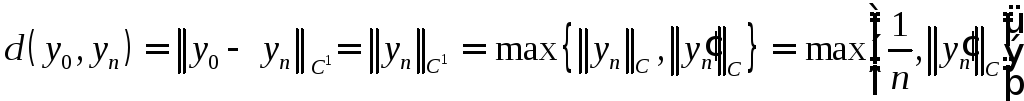 .
.
Но
![]()
![]() ,
так что
,
так что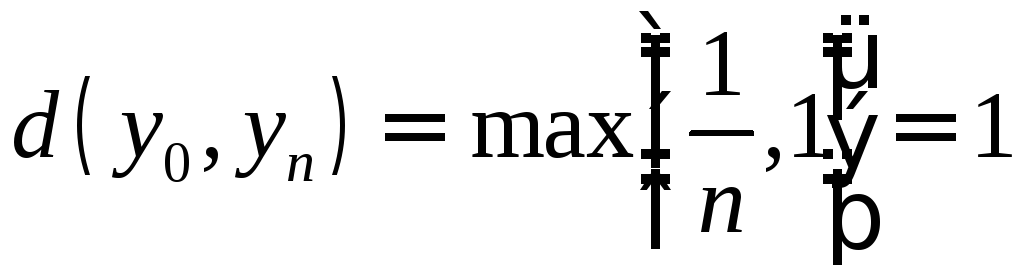 .
С возрастанием
.
С возрастанием![]() функция
функция![]() становится сколь угодно близкой к
функции
становится сколь угодно близкой к
функции
![]() по норме
по норме![]() ,
т.к.
,
т.к.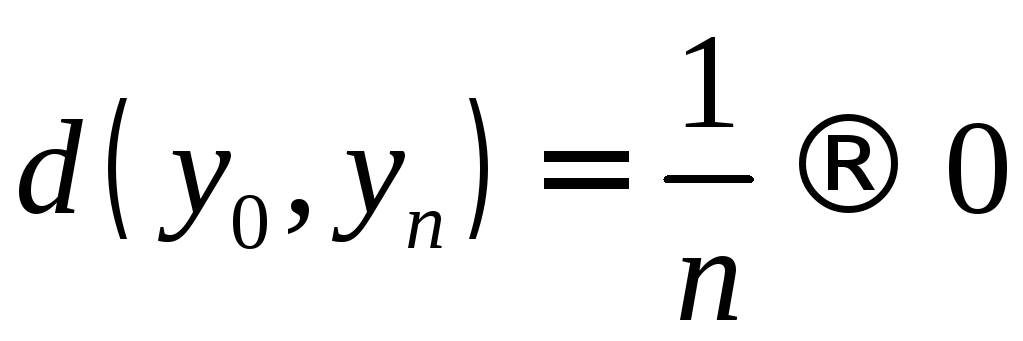 ,
тогда как всегда отстоит от неё на
расстояние
,
тогда как всегда отстоит от неё на
расстояние
![]() по норме
по норме![]() .
.
1.2.7.
Определение.
![]() окрестностью
окрестностью![]() точки
точки![]() пространства
пространства![]()
![]() называется множество точек (т.е. функций)
называется множество точек (т.е. функций)
![]()
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]()
![]()
т.е.
отстоящих от
![]() меньше чем на
меньше чем на
![]() .
.
|
|
|
и
![]() .
В пространстве
.
В пространстве![]() этого недостаточно: надо ещё, чтобы
изгибы кривой
этого недостаточно: надо ещё, чтобы
изгибы кривой![]() мало отличались от изгибов кривой
мало отличались от изгибов кривой![]() .
.
1.2.8.
Определение. Пусть
![]() множество
каких – либо функций. Отображение
множество
каких – либо функций. Отображение![]() ,
сопоставляющее каждой функции
,
сопоставляющее каждой функции![]() определенное число
определенное число![]() ,
называетсяфункционалом,
определенным на множестве функций
,
называетсяфункционалом,
определенным на множестве функций
![]() .
.
Отображение
![]() ,
сопоставляющее каждому набору из
,
сопоставляющее каждому набору из![]() функций
функций![]() (т.е.
вектор – функции
(т.е.
вектор – функции![]() )
определенное число
)
определенное число
![]() )
называетсяфункционалом,
определенным на множестве наборов
функций из
)
называетсяфункционалом,
определенным на множестве наборов
функций из
![]() (на
множестве вектор – функций).
(на
множестве вектор – функций).
В
п. 1.1 был
рассмотрен пример функционала
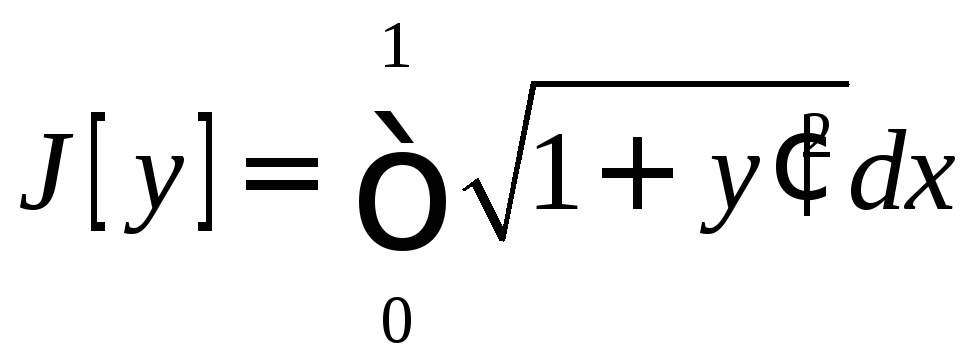 ,
определенного в пространстве
,
определенного в пространстве![]() .
Еще примеры:
.
Еще примеры:
Пусть
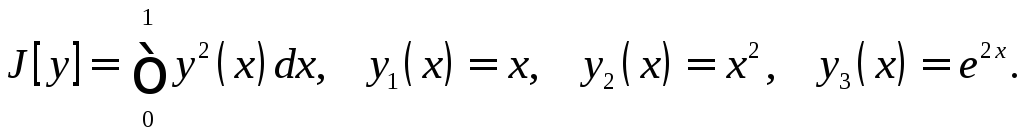
Тогда
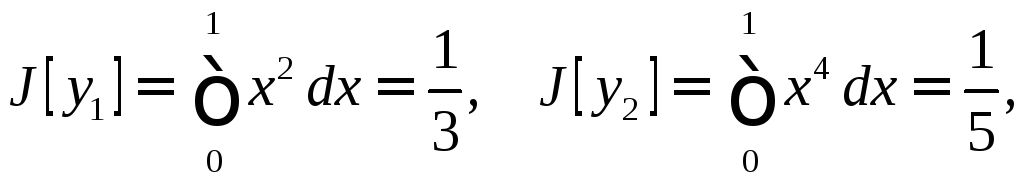
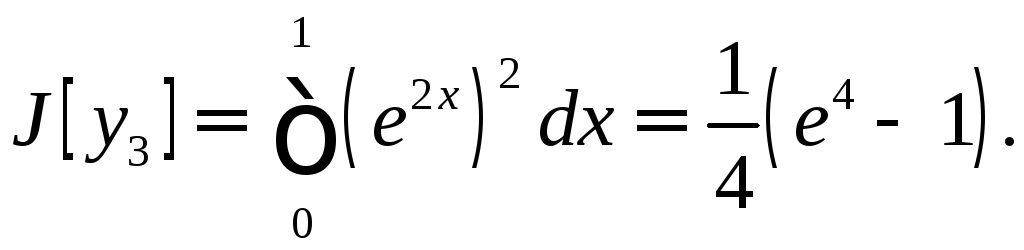
Пусть
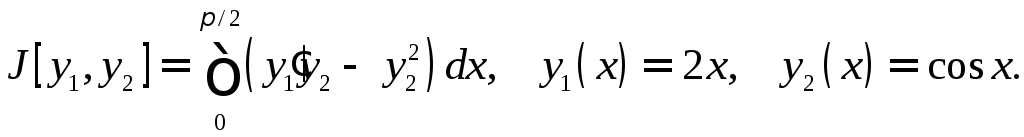
Тогда
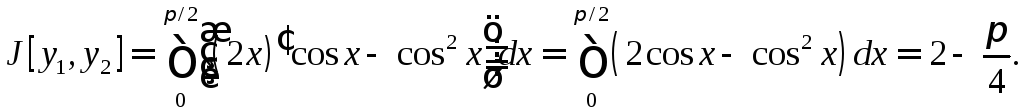
1.2.9.
Определение. Говорят,
что функционал![]()
определенный
на множестве
![]() допустимых вектор – функций
допустимых вектор – функций![]() с координатными функциями
с координатными функциями![]() ,
имеет в точке
,
имеет в точке![]() локальный
максимум (минимум), если
для всех
локальный
максимум (минимум), если
для всех
![]() ,
достаточно близких к
,
достаточно близких к![]() ,
выполняется неравенство
,
выполняется неравенство
![]()
![]() ,
т.е. существует
,
т.е. существует
![]() такое, что
такое, что
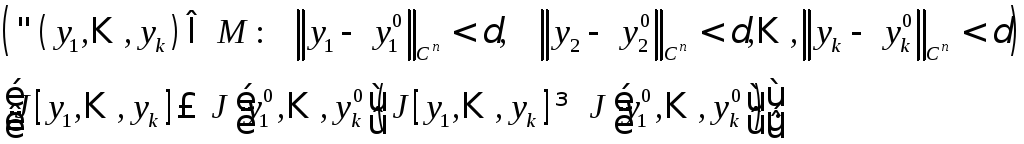
Для исследования функционала на экстремум введем понятие, аналогичное понятию производной числовой функции числовой переменной.
Пусть
функционал
![]() определен на некотором множестве
допустимых функций
определен на некотором множестве
допустимых функций![]() ,
и
,
и![]() фиксированные
допустимые функции. Рассмотрим числовую
функцию числовой переменной
фиксированные
допустимые функции. Рассмотрим числовую
функцию числовой переменной![]() (в предположении, что при любом
(в предположении, что при любом![]() функция
функция![]() остается допустимой функцией:
остается допустимой функцией:![]() ). Приращение аргумента
). Приращение аргумента![]() и просто
и просто![]() называютвариацией
аргумента.
называютвариацией
аргумента.
1.2.10.
Определение.
Если существует
производная функции
![]() в точке
в точке
![]() ,
то она называется
первой вариацией функционала
,
то она называется
первой вариацией функционала
![]() в точке
в точке![]() при данной вариации
при данной вариации![]() аргумента,
и обозначается
аргумента,
и обозначается
![]() :
:
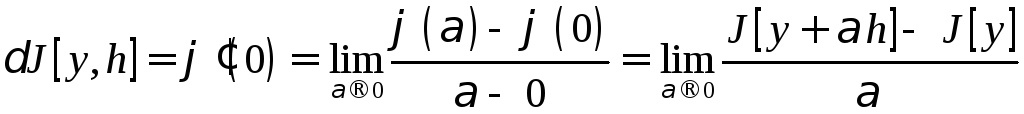
(заметим,
что в числителе стоит приращение
функционала
![]() в точке
в точке![]() ,
вызванное
приращением (вариацией)
,
вызванное
приращением (вариацией)
![]() аргумента.
При
аргумента.
При![]() это приращение аргумента стремится к
нулю:
это приращение аргумента стремится к
нулю:![]() =|
по определению 1.2.1|=
=|
по определению 1.2.1|=![]() ,
так как
,
так как
![]() ).
).
Для
функционала от
![]() функций (от
функций (от![]() мерной
вектор – функции)
мерной
вектор – функции)![]() производная функции
производная функции![]() в точке
в точке![]() являетсяпервой
вариацией функционала
являетсяпервой
вариацией функционала
![]() в точке
в точке![]() по аргументу
по аргументу![]() при данной вариации
при данной вариации![]() этого аргумента:
этого аргумента:
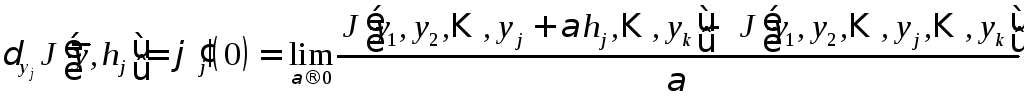 .
.
1.2.11. Теорема (необходимое условие локального экстремума функционала в терминах первой вариации).
Пусть
функционал
![]() ,
определенный на множестве
,
определенный на множестве![]() допустимых вектор–функций
допустимых вектор–функций![]() с координатами
с координатами![]() имеет в точке
имеет в точке![]() локальный экстремум. Если в этой точке
функционал имеет первую вариацию по
аргументу
локальный экстремум. Если в этой точке
функционал имеет первую вариацию по
аргументу![]() при какой-либо вариации
при какой-либо вариации![]() этого аргумента, то эта первая вариация
равна нулю:
этого аргумента, то эта первая вариация
равна нулю:
![]() .
.
□ Пусть,
например
![]() точка
минимума: существует
точка
минимума: существует![]() такое, что
такое, что
![]()
![]() .
Возьмем точку
.
Возьмем точку
![]()
![]() .
Для нее
.
Для нее
![]() .
При достаточно малом
.
При достаточно малом![]() будет
будет![]() ,
так как
,
так как![]() ,
где
,
где![]() .
Поэтому имеем
.
Поэтому имеем
![]()
![]() ,
,
т.е.
![]()
![]() ,
или
,
или![]() .
.
Таким
образом, при всех достаточно малых
![]() выполняется неравенство
выполняется неравенство![]() .
Это означает, что функция
.
Это означает, что функция
![]()
имеет
минимум в точке
![]() .
По условию, при данной вариации
.
По условию, при данной вариации![]() существует первая вариация по аргументу
существует первая вариация по аргументу![]() ,
т.е. существует
,
т.е. существует![]() .
Но, по теореме Ферма, если в точке
локального экстремума числовая функция
числового аргумента имеет производную,
то она равна нулю:
.
Но, по теореме Ферма, если в точке
локального экстремума числовая функция
числового аргумента имеет производную,
то она равна нулю:![]() .
.
Следовательно,
![]() .
■
.
■
Замечание.
Если найдена вектор – функция
![]() в которой первые вариации функционала
в которой первые вариации функционала![]() обращаются в нуль, то это ещё не значит,
что в точке
обращаются в нуль, то это ещё не значит,
что в точке![]() функционал действительно имеет экстремум:
ведь это необходимое условие экстремума.
Достаточные условия экстремума
функционала сложны, их не будем
рассматривать. Но если по смыслу задачи
экстремум есть, а найдена только одна
вектор – функция
функционал действительно имеет экстремум:
ведь это необходимое условие экстремума.
Достаточные условия экстремума
функционала сложны, их не будем
рассматривать. Но если по смыслу задачи
экстремум есть, а найдена только одна
вектор – функция![]() ,
в которой первые вариации обращаются
в нуль (“критическая точка”), то в точке
,
в которой первые вариации обращаются
в нуль (“критическая точка”), то в точке![]() обязан быть экстремум.
обязан быть экстремум.
В достаточных условиях экстремума используется понятие второй вариации функционала, которое мы не будем рассматривать. Поэтому в дальнейшем вместо “первая вариация” будем говорить просто “вариация”.