1.1.2. Лемма Лагранжа

Если функция непрерывна на отрезкеи

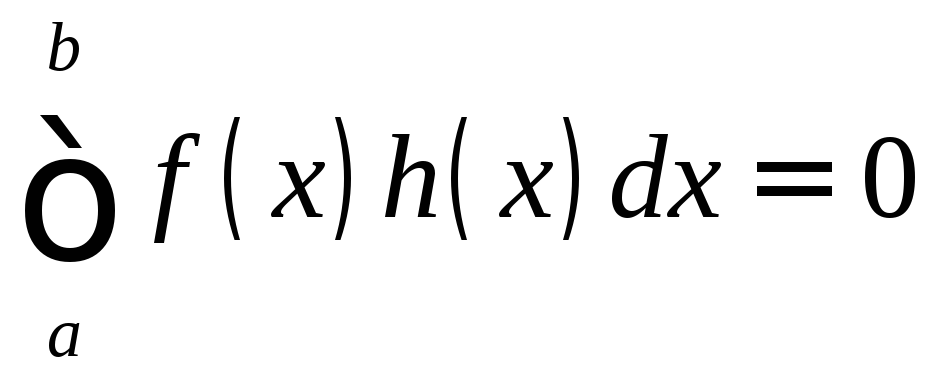(2)

при любой функции , бесконечно дифференцируемой на отрезкеи обращающейся на его концах в нуль:тона отрезке.

□ Допустим, что имеется точка , в которой, например. Тогда по свойству сохранения знака непрерывной функцией, в некоторой окрестности точкибудетнайдется отрезоктакой, что(илимогут совпадать с одним из концов отрезка).

По условию леммы, для функции , построенной в примере 1.1 для этого отрезка, равенство (2) тоже выполняется, но, посколькувне, то фактически.

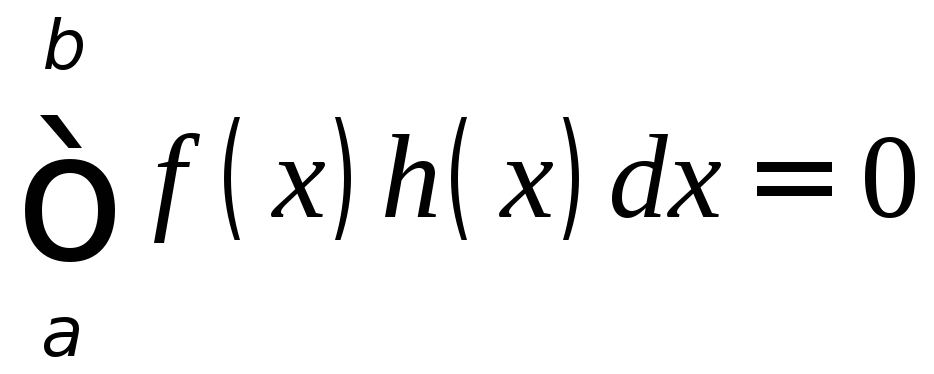C другой стороны . ВозьмемНа этом отрезке функциянепрерывна и отрицательна.

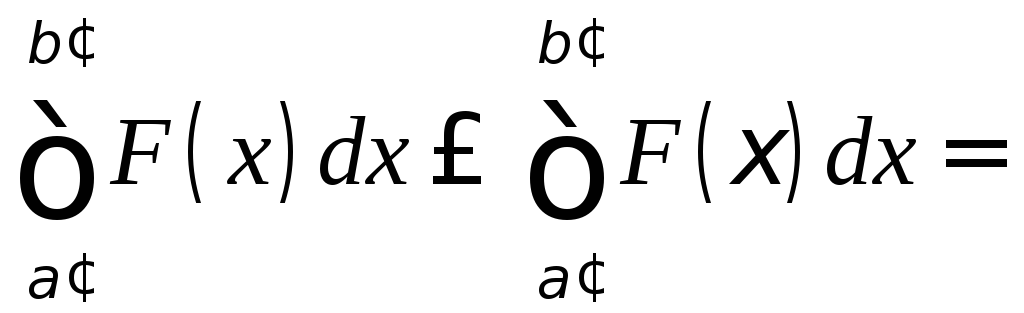
По теореме Вейерштрасса она имеет в некоторой точке максимальное значение , которое, конечно, тоже отрицательно: поэтому Значение этого интегралауменьшится, если добавим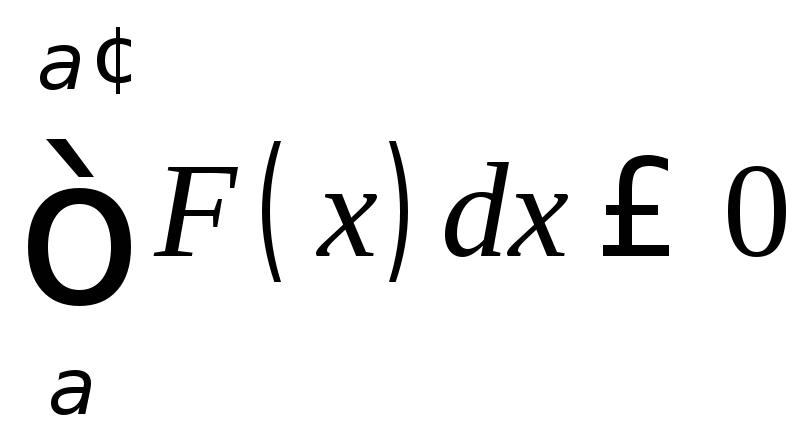и, так что тем более

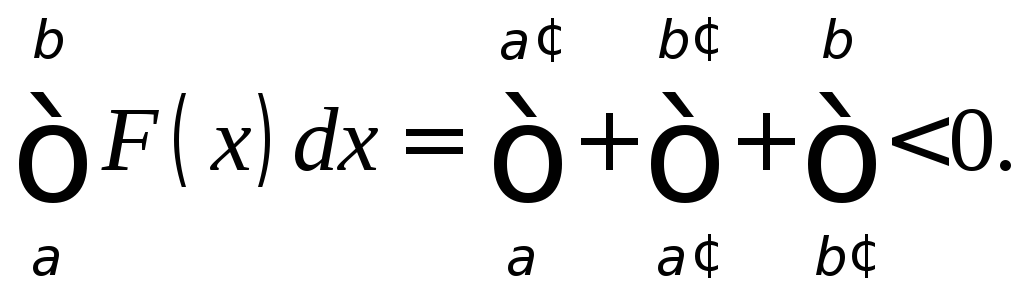
Таким образом, получим 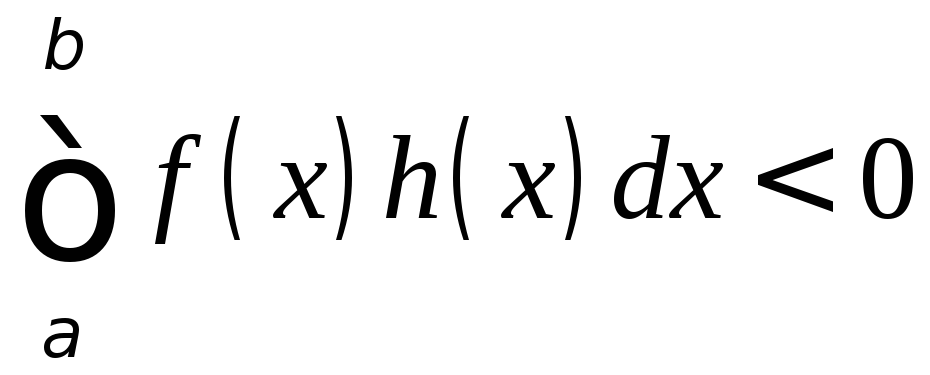, что противоречит равенству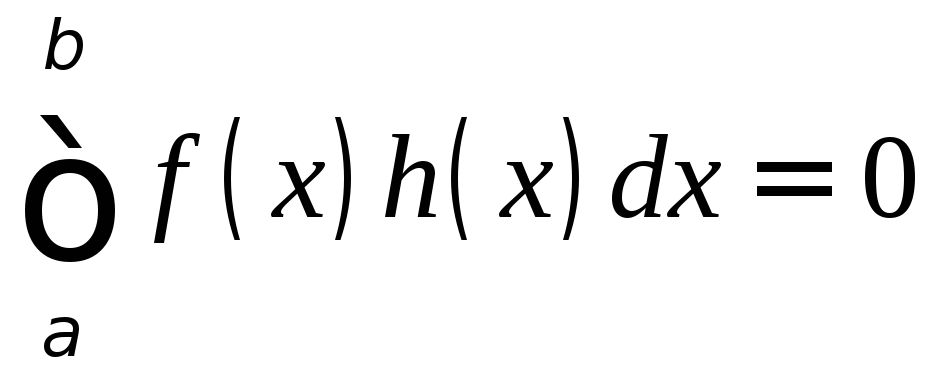. Следовательно, допущение неверно. ■

Следующую теорему сформулируем без доказательства.

1.1.3. Теорема Лейбница (о дифференцировании под знаком интеграла)

Если функция и её частная производнаянепрерывна в прямоугольнике, то.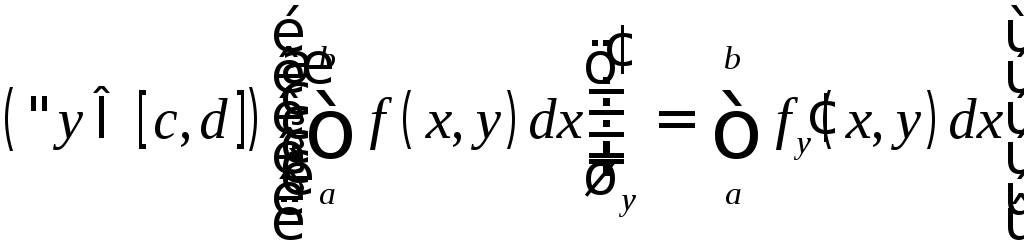

1.2. Основные понятия

Как известно из линейной алгебры, линейным пространством называется множество (с элементами произвольной природы), если в этом множестве введены двелинейные операции: операция сложения элементов , сопоставляющая им элемент этого же множества , называемыйсуммой и обозначаемый , и операцияумножения элемента на число , сопоставляющая им элемент этого же множества , называемый произведением элемента на числои обозначаемый , причем эти линейные операции удовлетворяют 8-ми аксиомам:

Для любых элементов и любых чисел:

1) (переместительность сложения),

2) (сочетальность сложения),

3) существует элемент такой, что(существование нулевого элемента),

4) для каждого существует элемент, обозначаемыйтакой, что(существование противоположного элемента),

5) (поглощение единицы),

6) (сочетательность умножения на число),

7) (распределительность умножения на число относительно сложения чисел),

8) (распределительность умножения на число относительно сложения элементов).

Примером линейного пространства является мерное арифметическое пространство

1.2.1. Определение. Линейное пространство называетсянормированным пространством, если каждому элементу поставлено в соответствие числонорма этого элемента – так, что для любых и любого числа

1) (неотрицательность),

2) (однородность),

3) (неравенство треугольника).

Примером нормированного пространства является евклидово пространство , в котором нормой элементаявляется его модуль(так что).

В нормированном пространстве можно ввести понятие расстояния между элементами.

1.2.2. Определение. Расстоянием между элементами x,y нормированного пространства L называется норма их разности: . В частности, так что норма элемента есть расстояние от этого элементадо нулевого элемента.

1.2.3. Теорема (о свойствах расстояния)

Число обладает свойствами:

1) (неотрицательность).

2) (симметричность),

3) (неравенство треугольника).

□ 1) (по определению 1.2.1)

(по определению 1.2.1).

2) (по определению 1.2.1) .

3) ( по определению 1.2.1) . ■

Мы будем иметь дело с множеством функций, непрерывных на отрезке , которое будем обозначать, и с множеством функций,раз непрерывно дифференцируемых на(т.е. имеющих непрерывные производные дого порядка включительно), которое будем обозначать. Если сложение функций и умножение функции на число понимать как обычно:

то при этих линейных операциях множества и являются линейными пространствами. Например, если, т.е. имеют непрерывные производные, то сумма, тоже непрерывно дифференцируема на, т.е.еслитотоже непрерывно дифференцируема на, т.е.Легко проверить, что эти линейные операции удовлетворяют всем 8 аксиомам линейного пространства, так как при каждом фиксированномсложение функции и умножение функции на число сводится к сложению и умножению чисел, а для чисел все аксиомы выполняются. Нулевым элементом пространстваявляется функция, тождественно равная нулю наПротивоположным элементом для функцииявляется функция.

Аналогично, тоже является линейным пространством.

Итак, иявляются линейными пространствами с обычными правилами сложения функций и умножения функции на число.

Введем нормы элементов в этих пространствах, что позволит ввести понятие расстояния между элементами этих пространств (т.е. между функциями).

Норма есть расстояние от функциидо функции. Впространстве непрерывных функций естественно считать функцию близкой к функции (на всем отрезке

!) если близко к нулю значение (такое максимальное значение при некоторомсуществует в силу теоремы Вейерштрасса для функции, непрерывной на отрезке).

Поэтому положим .

1.2.4. Теорема (о норме )