3.4. Задачи с подвижными границами

Дан функционал

и условия .

Схема решения:

1. Из уравнения Эйлера находим.

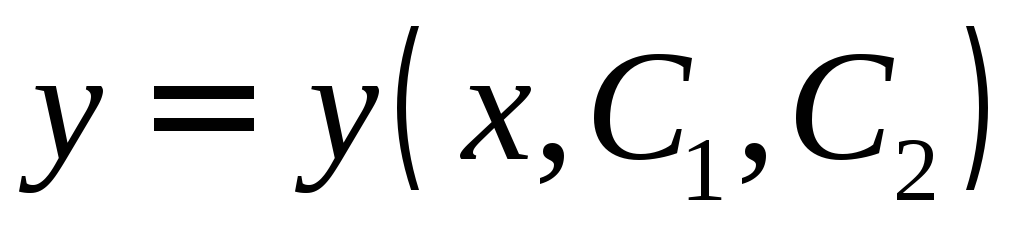2. Запишем условия трансверсальности

и уравнения связи

3. Решаем их совместно и определяем и концы отрезка.

Замечание: Если на одном из концов искомой кривой задано обычное граничное условие, т.е.или, то условие трансверсальности следует записать только для другого конца кривой.

Задача 1.

.

□ .

Уравнение Эйлера .

Условие трансверсальности

т.к. то

Ответ: .■

Задача 2.

.

□ .

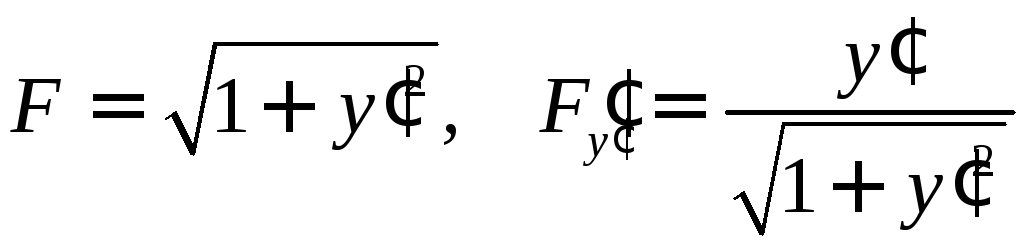Уравнение Эйлера , тогда, тогда.

Условия трансверсальности совместно с уравнениями связи, учитывая, что и:

Решаем совместно и получаем

.

Ответ: .■

Если граничное условие для не дано, то записываем естественное граничное условие

.

Задача 3. Найти экстремали функционала

.

□ 1. Уравнение Эйлера ,

.

2. .

Получаем систему

. ■

3.5. Варианты заданий: «Задачи с подвижными границами»

В каждом варианте (N) решить две задачи.

1. Дано: и.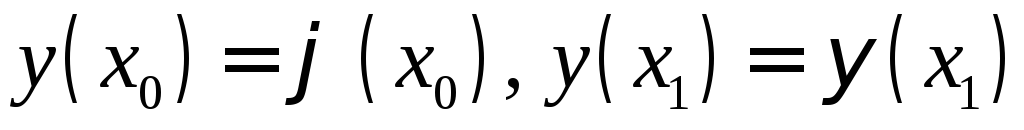

Найти и концы отрезка, (если, тогда).

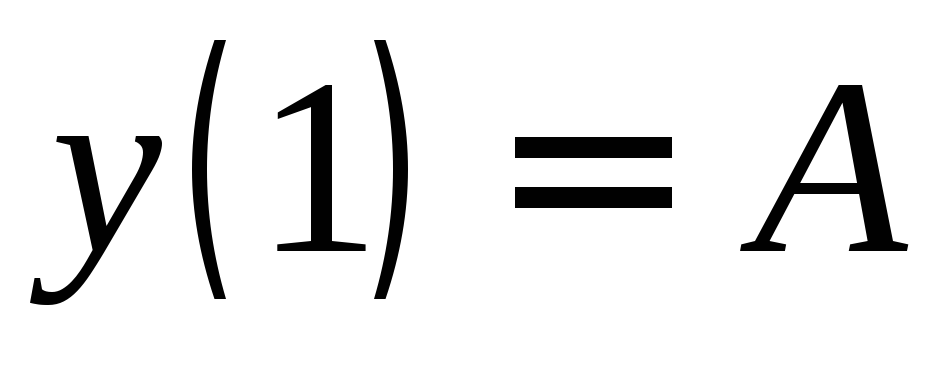2. Дано: и. Найти.

N
1.					4
2.					5
3.					1
4.					3
5.					5
6.					1
7.					0
8.					4
9.					6
10.					1
11.					2
12.					3
13.					7
14.					2
15.					3
16.					6
17.					8
18.					9
19.					3
20.					5
21.					2
22.					7
23.					5
24.					7
25.					3

3.6. Варианты заданий: «Задачи по оптимальному управлению»

1. Остановка точки, движущейся по инерции, в заданной точке за кратчайшее время.

N
1	-2	2	-2	1
2	-2	0	-2	1
3	-2	-2	-2	1
4	1	2	-2	1
5	1	1	-2	1
6	0	1	-2	1
7	0	-1	-2	1
8	-2	1	-1	2
9	-2	-1	-1	2
10	-2	0	-1	2
11	1	1	-1	2
12	1	-1	-1	2
13	2	0	-1	2
14	-1	1	-2	2
15	-1	0	-2	2
16	-2	-1	-2	2
17	1	-1	-2	2
18	1	2	-2	2
19	0	2	-2	2
20	0	-2	-2	2
21	-2	1	-1	1
22	-1	1	-1	1
23	-2	0	-1	1
24	2	0	-1	1
25	2	1	-1	1

2. Остановка математического маятника в верхнем положении неустойчивого равновесия за кратчайшее время.

N
1	-0,2	-0,4	-2	1
2	-0,2	0,8	-2	1
3	-0,2	1	-2	1
4	0,2	-0,8	-2	1
5	0,2	-1	-2	1
6	-0,2	-0,4	-2	1
7	-0,2	0,4	-2	1
8	-0,2	1	-1	2
9	-0,2	2	-1	2
10	0,2	0,2	-1	2
11	0,2	-0,4	-1	2
12	0,2	-1	-1	2
13	0,2	-0,4	-1	2
14	-0,2	1	-2	2
15	-0,2	0,1	-2	2
16	-0,2	0,6	-2	2
17	0,2	0,2	-2	2
18	0,2	-1,2	-2	2
19	0,2	0,2	-2	2
20	-0,2	0,4	-2	2
21	-0,2	2	-1	1
22	0,2	-0,7	-1	1
23	0,2	-0,2	-1	1
24	0,2	0,4	-1	1
25	-0,2	-0,4	-1	1

93