2.2. Линейная стационарная задача

оптимального быстродействия.

Мы рассмотрим только случай, когда закон движения (т.е. система дифференциальных уравнений) не содержит явно время:

(1)

(время скрыто в функцияхи). В этом случае скоростьв точкене зависит от времени. Поэтому, отправляясь из этой точки в разные моменты времении, за один и тот же промежуток времени точка опишет одну и ту же траекторию и попадет в одну и ту же точку (так ведут себя, например, частицы жидкости при установившемся течении). Система дифференциальных уравнений (1), не содержащее явно время, называетсястационарной или автономной системой.

Кроме того, мы рассмотрим случай, когда система (1) линейная (первой степени относительно переменных ):

,

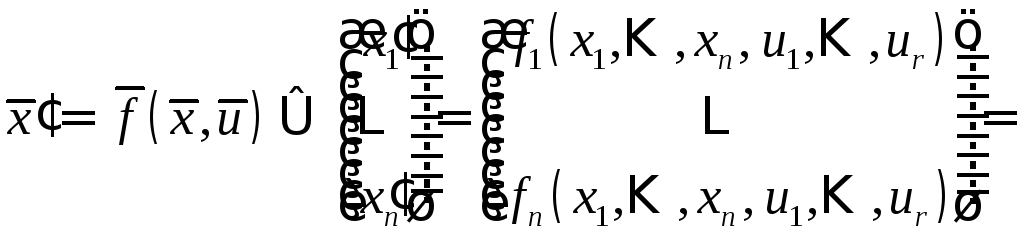
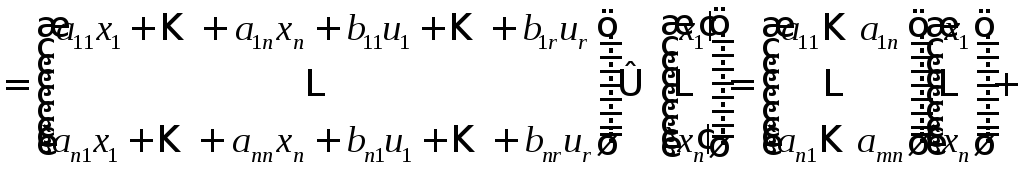
где известная постоянная- матрица,

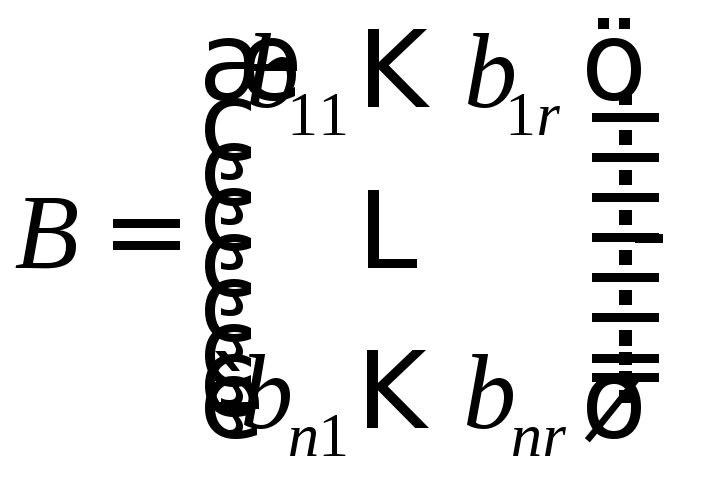известная постоянная - матрица (матрица управления).

Таким образом, мы рассматриваем линейную стационарную задачу

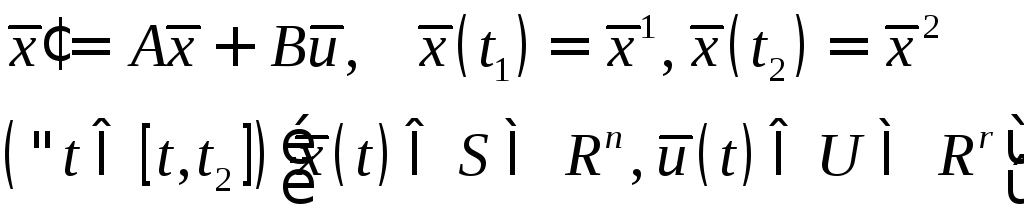(2)

где искомаямерная вектор-функция, непрерывная с кусочно-непрерывной производной,мерное кусочно-непре-рывное управление.

Сформулируем без доказательства критерий управляемости задачи (2).

2.2.1. Теорема (критерий Калмана)

Линейная стационарная задача (2) управляема (т.е. найдется допустимое управление , переводящее объект (1) из состоянияв состояниепри любых) тогда и только тогда, когда

.

Под матрицей понимается матрица, полученная приписыванием справа к матрицеэлементов матрицы(с сохранением порядка элементов), затем элементов матрицыи т.д.

Пример. Проверим управляемость задачи

.

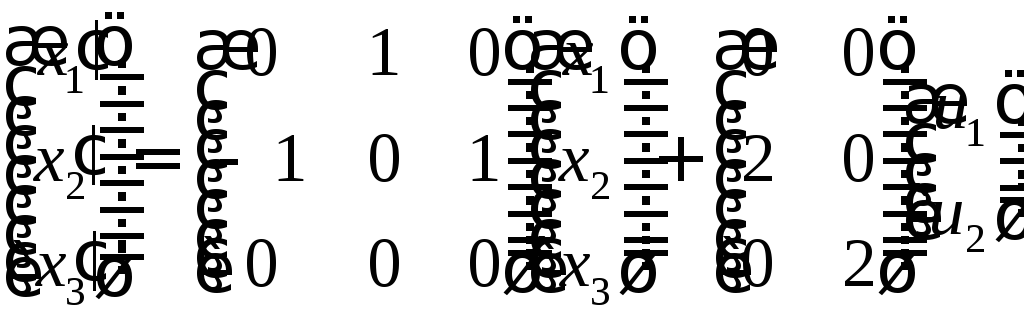Здесь ,

, .

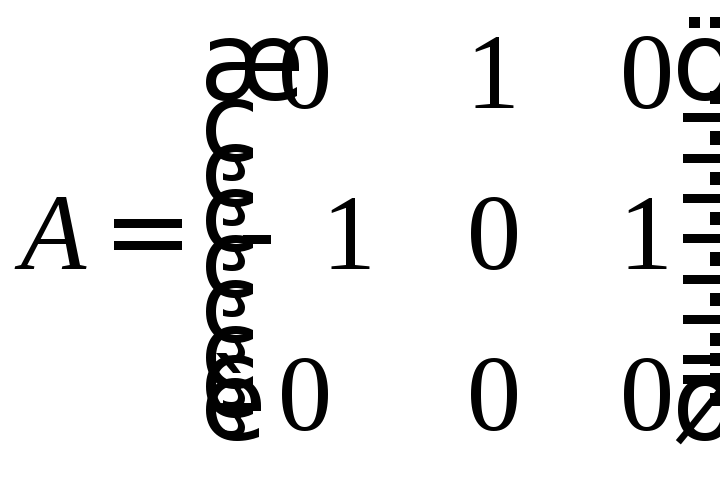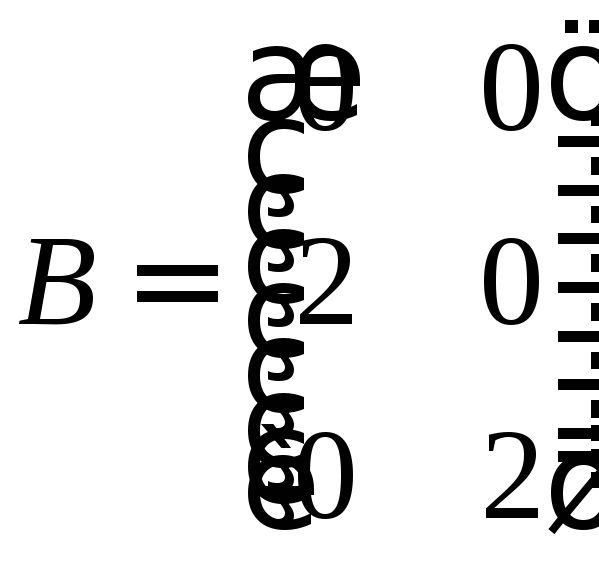Составим матрицу :

,,

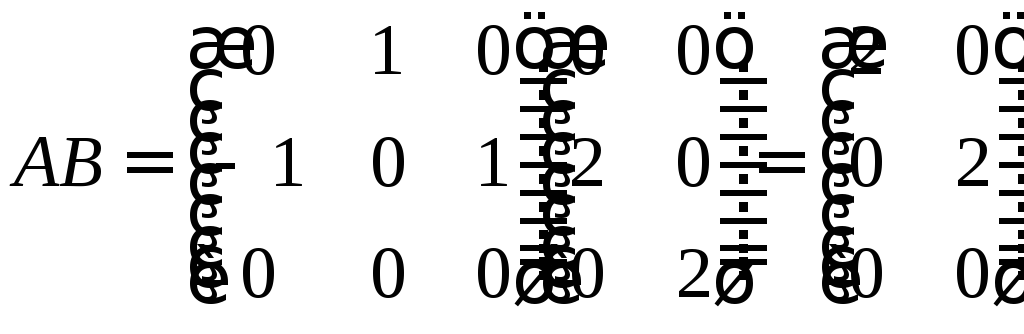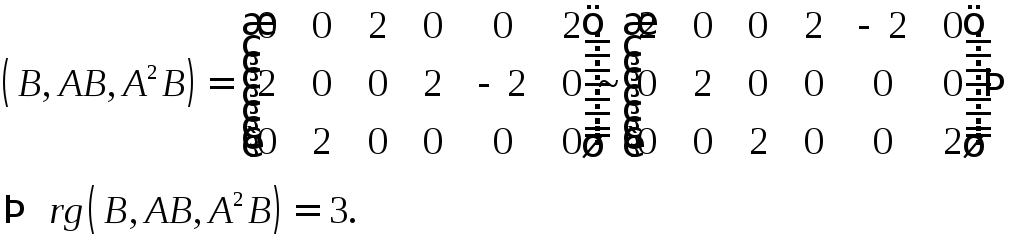
Задача управляема.

В качестве критерия качества будем брать интегральный критерий

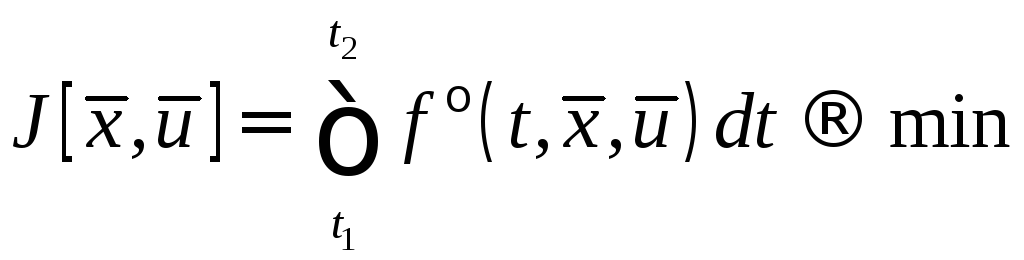
с подынтегральной функцией :

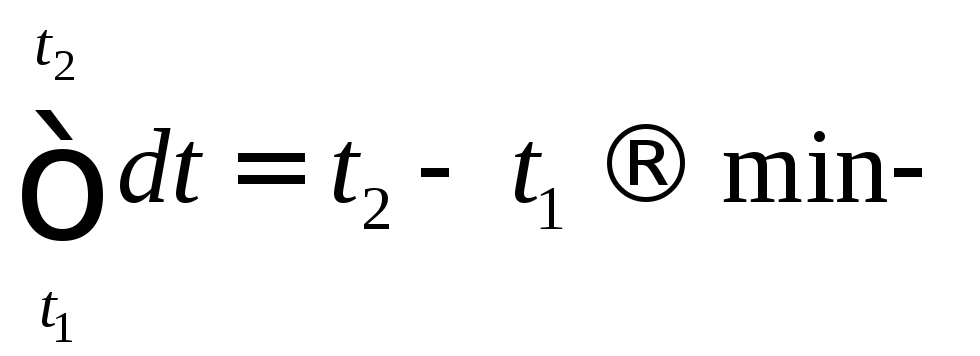критерий оптимального быстродействия.

Для линейной стационарной задачи оптимального быстродействия

сформулируем принцип максимума Понтрягина. В этой задаче фиксированный начальный момент времени, конечный момент временине фиксирован: его предстоит найти так, чтобы промежуток времени, в течение которого объект перейдет из состоянияв состояние, был минимальным (это достигается за счет выбора оптимального управления).

2.2.2. Определение.

Пусть дана однородная линейная система дифференциальных уравнений

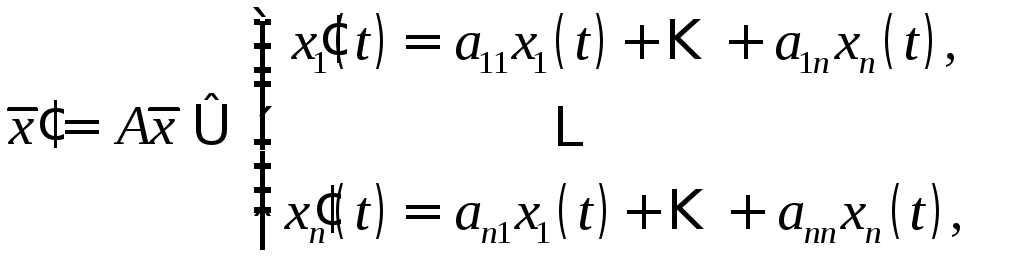где

.

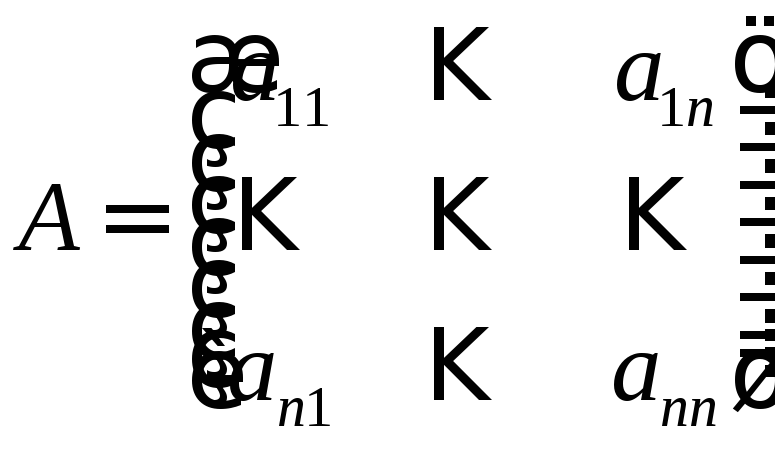Однородная линейная система дифференциальных уравнений

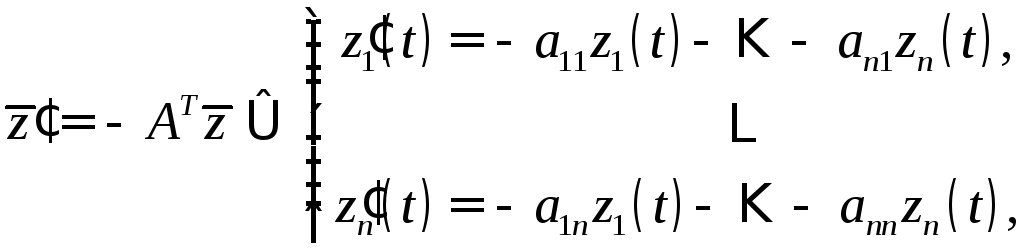(3)

где транспонированная матрица, называетсясопряженной системой для данной системы .

Общее решение системы (3) содержит произвольных постоянных:

,

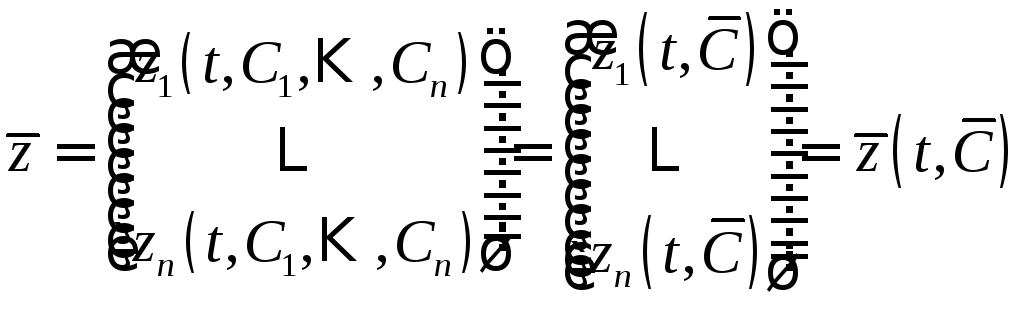т.е. содержат произвольный постоянный мерный вектор.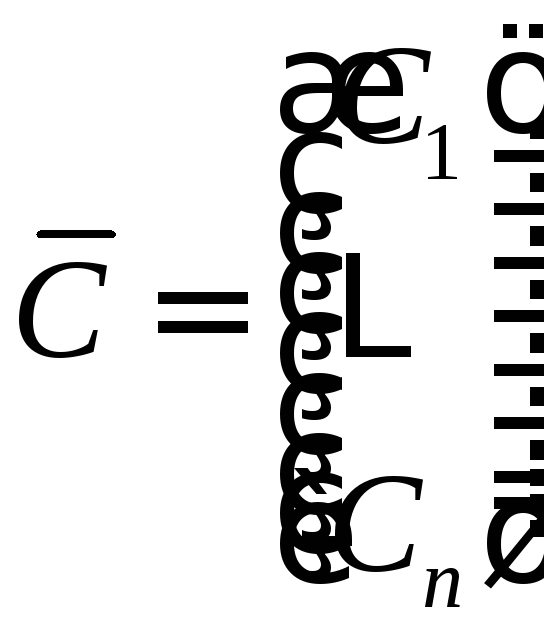

2.2.3. Определение.

Функция , где- общее решение сопряженной системы(3), 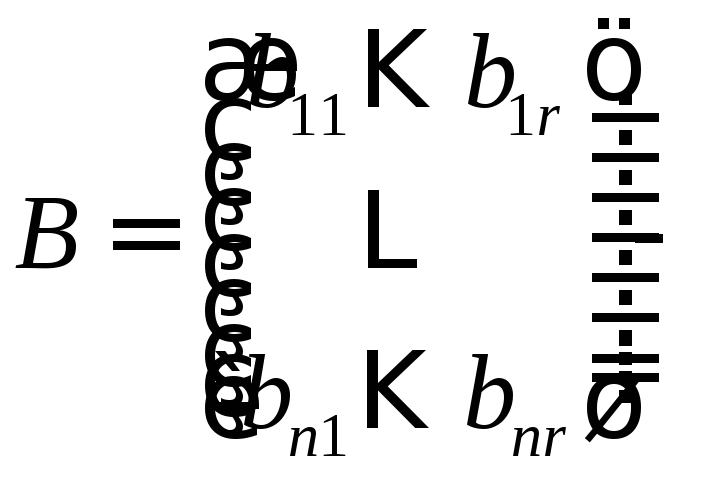матрица управления,управление, называется функцией Понтрягина.

При фиксированном значении момента времени и постоянного векторазначение функции Понтрягина зависит от значения управленияв точке: при выборе разных значений управления в фиксированной точкефункция Понтрягина принимает разные значения.

Формулируем без доказательства принцип максимума Понтрягина:

2.2.4. Теорема (принцип максимума Понтрягина).

Пусть на отрезке при некотором постоянноммерном векторедопустимые значения управления(т.е.) выбраны так, что выполняетсяпринцип максимума Понтрягина:

При каждом фиксированном , за исключением, может быть, конечного числа значений,

1) значение функции Понтрягина является максимальным среди значений, принимаемых при всех других допустимых значениях управления:

,

2) это максимальное значение положительно:

Тогда управление наявляется оптимальным в смысле быстродействия.