29.Производная показательной неявной функции. Производные высших порядков:

Производная показательной функции:

При для любого х

Производная неявной функции:

При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение . Отсюда получим формулу для производной функции , заданной неявно: = . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением :

, .

Производные высших порядков:

Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f (n)(x) = (f (n -1)(x))'

30. Теорема Лагранжа. Правило Лопиталя.

Теорема Лагранжа: Пусть задана ф-я и пусть она: 1) опр-на и непрер на ; 2) имеет кон произв-ю на . Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во

Док-во: Введём вспомогат функцию

Она удовл-т всем условиям теоремы Ролля. Действительно, F(x) опред-на и непрер на , ,

,т.е. сущ на . След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.

или

Тогда ∆

Правило Лопиталя: Пусть ф-и f(x) и g(x) одновр явл либо бескон б-ми, либо беск-но малыми в т. . Тогда при выч-и пределов при x → для раскрытия неопред-тей вида или удобно применить пр. Лопиталя :

, Неопределенности вида 0 · ∞, ∞ – ∞, , , часто удается свести к неопределенностям вида или с помощью различных преобразований.

31. Достаточное усл-е возраст-я (убыв-я) ф-й.

Ф-я наз-ся возраст-ей на инт-ле , если для любых и из этого инт-ла, для которых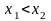 , верно нерав-во . Ф-я наз-ся убыв-ей на инт-ле , если для любых x₁ и x₂ из этого инт-ла, для кот , верно нерав-во .Необх-ое усл-е возраст-я ф-ии:если ф-ия диффер-ма и возраста на инт-ле , то для всех х из этого инт-ла.Необх-ое усл-е убыв-я ф-ции. Если ф-ция дифф-ма и убыва на инт-ле , то для всех х из этого инт-ла.Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я диф-ма на инт-ле . Если во всех точках этого инт-ла , то ф-ия возраста на этом интле, а если , то ф-я убывает на этом инт-ле.

32. Экстремумы ф-й.

Точка x = x0 называется точкой максимума, а число — максимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с x0 , выполняется неравенство .

Точка x = x0 называется точкой минимума, а число — минимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с точкой x0 , выполняется неравенство .

Точки максимума и минимума называются точками экстремума.

Необходимое условие существования экстремума

Если x0 — точка экстремума, то производная в этой точке равна нулю или не существует.

33. Достаточное условие существования экстремума

Если функция y=f(x) непрерывна в точке x = x0 , дифференцируема в некоторой окрестности этой точки, и при переходе через точку x0 производная 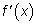меняет знак, то x = x0 — точка:

а) — максимум, если , при

и , при /

б) — минимум, если , при

и , при .

Алгоритм нахождения наибольшего и наименьшего значения функции одной переменной:

Находится область определения функции.

Находится производная.

Определяются критические точки.

Выбираются из критических точек те точки, которые принадлежат отрезку.

Считаются значения функции в критических точках принадлежащих отрезку и на концах отрезка.

Среди полученных значений функции выбираются самое большое и самое маленькое.