7. Критерий совместимости слау:

Теорема Кронекера-Капелли

Для того, чтобы СЛАУ, где AX=B, где матр A разм-ти m*n была совместной необх-мо и дост-но, чтобы ранг осн матр системы был равен рангу расшир матр системы.

r(A) = r(A/B)

Док-во:

Необходимость: пусть СЛАУ AX=B совместна.

Доказать, что ранги равны.

Сущ набор чисел (α1, α2…..αn), что будучи подставл в каждое из ур-й системы получим:

a11α1 + a12α2 + . ………. + a1nαn = b1

a21 α1 + a22α2 + … …… + a2n αn = b2

am1α1 + am2 α2 + ………… + amnαn = bm

Рассмотрим расширенную матрицу системы

0

0

…

0

b1

b2

…..

bm

a11 a12 ….. a1n

a21 a22…….. a2n

am1 am2…… amn

A

―—”——

(А/В)=

~

След-но r(A/B) = r(A)

Док-ть, что СЛАУ совместна, если ранги равны.

b1

b2

br

a11 a12 …. a1r…a1n

0 a22 ….. a2r…a2n

0 0 ….. arr.....arn

Дано: r(A/B) = r(A) и к расшир матрице (A/B) применим преобраз-я Гаусса. В рез-те расшир матр (A/B) будет приведена к виду верхней треуг или трапециев. А тогда реш-я сист м. б. пол-ны обр м-м Г-са.

Случай 1. r(A)≠r(A/B), то СЛАУ несовместна.

Случай 2. r(A/B)=r(A)=n –СЛАУ совм и имеет единств реш-е.

Случай 3. r(A/B) = r(A)=r < –СЛАУ совм и имеет беск мн р-й.

8. Матричный метод

Пусть дана система из 3-х уравнений с тремя неизвестными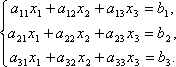 . 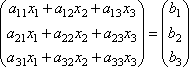Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.

9. Метод Крамера.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: Находим det

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём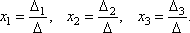

10. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

• перестановка строк или столбцов;

• умножение строки на число, отличное от нуля;

• прибавление к одной строке другие строки.

• Удаление нулевой строки

Любая СЛАУ может быть преобразована к виду системы, у которой расширенная матрица будет иметь ступенчатый вид.

Приведение системы к ступенчатому виду или расширенную матрицу к виду трапециевидной называется прямой ход Гаусса. Обратный ход – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Придавая неизвестным (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными).