2.Опред-ль 1,2,3 порядков.

Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем следующим образом:

1. n=1. A=(a₁); det A=a₁

2. n=2.

3. n=3.

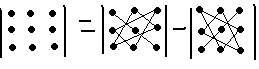
Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали:

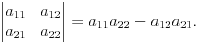
Определителем третьего порядка называется следующее выражение: Правило треугольников:

Пример: А= det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9

3. Определитель квадратной матрицы порядка n.

Определитель квадратной матрицы n-ного порядка равен алгебраической сумме парных произведений элементов i-той строки матрицы А на их алгебраические дополнения или j-го столбца на их алгебраические дополнения.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

4.Свойства определителей.

1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то det

этой матрицы равен 0

2)При транспонировании матрицы её определитель не изменяется: (detА =detА')

3) При перестановке местами 2-х строк или столбцов матрицы её

определитель меняет свой знак на противоположный

4) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0.

5)Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0.

6) Определитель матрицы не изменяется если к элементам одной строки (или столбца) прибавить элементы другой строки (или столбца), умноженные на одно и то же число

7) Общий множитель строки или столбца можно выносить за знак определителя

8) Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

Доказательство – проверкой.

9) det верхней треуг. матрицы = произведению диагональных эл-тов.

10) det A*B=detA*detB

11. Определитель верхней треугольной матрицы равен произведению диагональных элементов. A11 A22 Ann

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен (алгебраическое дополнение Aij=(-1)i+jMij. Здесь минор Mij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца)

5.Обратная матрица

Обр матр — такая матр A^-1, при умн-и на кот исходная матрица A даёт в результате единичную матрицу E:

AA⁻¹ = A⁻¹A = E

Теорема : для того, чтобы для кв.м.А сущ-ла обр, дост-но чтобы опр-ль этой м. был отличен от 0.(Кв матр обратима тогда и только тогда, когда она невырожденная, т.е. её опр-ль не равен 0. Для некв матриц обр матриц не сущ-т.)

Доказательство:

Необходимость. Пусть для матрицы A существует обратная матрица A^-1.

detA^-1*A=detE => detA≠ 0.

Д остаточность.

по м.А строим А^*

где А^* - м. алгебраических дополнений А^*

транспонируем полученную матрицу: (А^*)^Т=

найдем А* (А^*)^Т=С, Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

следовательно А* (А^*)^Т=detA*E => =>

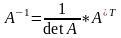
Сформ-м правило нах-я обр матр на примере матр А.

1. Находим опр-ль матр. Если Δ ≠0, то матр A^-1 сущ-т.

2. Составим матрицу A^* алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице A^* элементом i - ой строки и j - го столбца будет алгебраическое дополнение Aij элемента aij исх матрицы.

3. Транспонируем матрицу A^* и получим A^*T

4)

5 проверка A^-1*A=E

6.Минор к-го порядка матрицы. Базисный минор матр. Ранг матр и его св-ва. Теорема о ранге матр. Вычисление ранга.

А - прямоуг матрица размеров m*n.

Выбираем в матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель полученной матрицы называется минором k-го порядка матрицы А.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Наибольший из порядков миноров данной матрицы, отличный от нуля, называется рангом матрицы. (обозначается r(A))

нек. св-ва: 1) r(A)=0 => A=0

2)

3) ранг верхней треугольной м. = числу диагональных эл-тов гл. диагонали неравных нулю.

ранг трапециевидной матрицы= числу диагональных эл-тов главного базисного минора.

Ранг матр не изменится от след преобр-й, наз элемент преобраз-ми матрицы

: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой =0; - умножения строки на число, отличное от 0; - прибавления к эл-м строки соответствующих Эл-ов другой строки, умнож на одно и то же число. Ранг находят привидением её к треуг(трапециев) виду с пом этих элемент преобраз-ий

Теорема о ранге: наивысший порядок отличных от 0 миноров матрицы равен рангу этой матрицы