21. Предел числовой последовательности (чп).

ЧП – это ф-ия натур аргумента x_n=f(n),где n принадлежит N.

X1, x2,…xn,…-числ послед.(1), xn-общ член чп.

Число а наз пределом посл-ти, если для любого малого положит числа ξ > 0 сущ такой номер N, зависящий от ξ, что для всех номеров n>N выполняется неравенство |x_n-а|< ξ.

Замечание. |x_n-а|< ξ=> а- ξ<x₁<а+ ξ, X_n- ξ<a<x_n+ ξ – ξ окрестности т.а

Если число а-предел ЧП(1), то все члены посл-ти, начиная с некот номера N, попадают в ξ-окрестность т.а.Чем больше N,тем ниже а.

Если а-предел числ. послед-ти(1), то пишут: lim x_n=a или x_n→a, n→∞

Свойства числ. последовательности:

1.Если ЧП с общ членом x_n имеет предел, то она наз сходящейся.Всякая сход посл-ть огран, т.е. сущ M>0, что все члены этой П по модулю не превосх это число. |x_n |<М

2. Пусть заданы 3 П, x_n, y_n, z_n-общие члены. Причем lim x_n= lim z_n=а и выполняется неравенство: x_n ≤y_n≤z_n, то lim y_n=а.

3. Пусть послед. x_n, y_n имеют конечные пределы lim x_n=а lim y_n=в -∞<а,в<+∞. Тогда:

1. lim(x_n±y_n)= limx_n ± lim y_n)-справ для люб кон числа П

2. lim(x_n*y_n)= limx_n*limy_n

3. lim(Cx_n)=C limCx_n=C*a.

4. lim = = , b≠0.

Посл α_n наз бескон малой, если ее предел = 0, т.е. limα_n=0

Послед. β_n наз бесконечно большой, если ее предел = ∞.

Утверждение.Если послед. α_n-беск. малая, то послед. - беск. большая и наоборот.

В курсах матанализа док-ся, что П {Хn}= монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim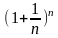 , причем е=2,718.

22.Предел ф-и на беск-ти и в точке. Одностор пр-лы.

Пусть задана ф-я y=f(x), кот опр-на на мн-ве х. Пусть - пред точка мн-ва х. Выберем на мн-ве х произв посл-ть чисел , кот не совп-т с , сход к .

Вычислим значение функции в каждой точке:

О.1(по Гейне). Число А наз-ся пред-м ф-ции у=f(x) при

(или в т-е ), если для любой сходящейся последовательности(1) соответствующая последоват-ть значений ф-ции(2) сходится к числу А.

О.2(по Коши) Число А наз пределом ф-и y=f(x) при (или в т-е ), если для люб сколь угодно малого положит числа сущ такое число >0, завис от , что для всех х, удовлетв нер-ву , вып-ся нер-во

или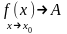

Ч исло А наз левостор пределом ф-и y=f(x), если вып-ся условие:

Число А наз правостор пределом ф-ции y=f(x), если вып-ся условие:

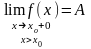
Замечание: если в качестве =0, то левосторонний предел: или ;

Правосторонний:

или

23. Бесконечно малые и бесконечно большие функции

О: Функция у = а(х) называется б.м. при х а, если

Функция называется б.б. при

если для любого числа М > 0 существует такое число зависящее только от М, что из неравенства

Следует неравенство

Символическая запись определения:

Между б.м. и б.б. функциями существует тесная связь.

24.Осн теоремы о пределах.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

Следствие 1. Постоянный множитель можно выносить за знак предела.

Следствие 2. Предел степени равен степени предела

Теорема 3. Предел частного двух функций равен частному пределов этих функций.

Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если , то .

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы , то имеет место неравенство b≥c.