3.9. Формула Тейлора

Теорема. Если функция раз дифференцируема в точке , то в некоторой достаточно малой окрестности этой точки имеет место разложение функции

,

называемое формулой Тейлора -го порядка для функции в окрестности точки .

Здесь многочлен

называется многочленом Тейлора -го порядка, а разность функции и многочлена

– остаточным членом формулы Тейлора.

,

где – бесконечно малая более высокого порядка малости по отношению к , т.е. к -ой степени приращения переменного. Это означает, что функция стремится к нулю быстрее своего аргумента:

.

Таким образом,

.

Если отбросить остаточный член, то получим формулу приближенного вычисления функции через многочлен Тейлора для точек , близких к точке : .

Частный случай формулы Тейлора при называется формулой Маклорена:

.

Примеры разложений элементарных функций по формуле Тейлора.

1. Разложение экспоненциальной функции в окрестности нуля:

2. Формула Тейлора для функции в окрестности нуля имеет вид:

3. Разложение другой тригонометрической функции в окрестности нуля содержит в отличие от функции только четные степени переменного:

4. Приведем также разложение по формуле Маклорена логарифмической функции :

3.10. Условия монотонности и существования экстремума

Критерий монотонности дифференцируемой функции. Для того, чтобы дифференцируемая на интервале функция не убывала (не возрастала) необходимо и достаточно, чтобы ее производная во всех точках интервала была неотрицательной (неположительной).

Достаточное условие строгой монотонности дифференцируемой функции. Если производная во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает).

Непосредственно из теоремы Ферма следует

Необходимое условие экстремума. Если функция определена в окрестности точки и достигает в ней локального экстремума, то производная функции либо существует и равна нулю, либо не существует.

Точки, в которых производная равна нулю или не существует, называются критическими.

Замечание. Из равенства нулю производной, вычисленной в некоторой точке, в общем случае не следует, что в точке достигается локальный экстремум.

Пример. Производная функции в точке равна нулю, но в этой точке нет локального экстремума.

Достаточные условия экстремума. Пусть функция дифференцируема в окрестности , за исключением, быть может, самой точки . Тогда:

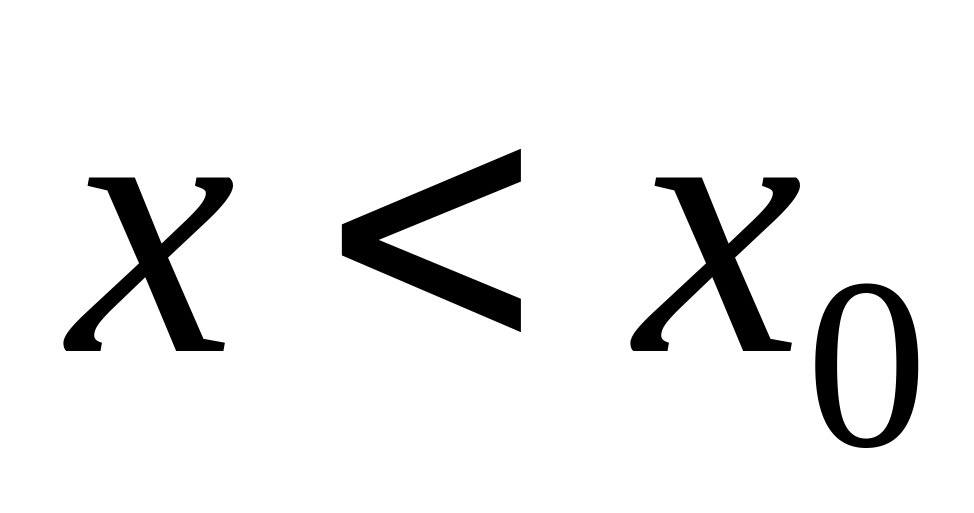1. если для всех точек и для всех точек (производная меняет знак с плюса на минус при переходе через точку ), то – точка строго локального максимума,

2. если для всех точек и для всех точек (производная меняет знак с минуса на плюс при переходе через точку ), то – точка строго локального минимума.

Приведем достаточные условия локального экстремума функции в терминах производных высших порядков.

Пусть функция раз дифференцируема в точке , , и производные до -го порядка включительно в этой точке равны нулю:

,

а производная .

Тогда,

1. если -четное число и , то - точка строгого локального минимума функции,

2. если -четное число и , то - точка строгого локального максимума функции,

3. если -нечетное число, то не является точкой локального экстремума.

В частности:

Если функция дважды дифференцируема в точке , то

1. - точка строгого локального минимума функции, когда ,

2. - точка строгого локального максимума функции, когда .

Таким образом, если в критической точке существует производная второго порядка, и она отлична от нуля, то точка является точкой строгого локального экстремума. Знак производной второго порядка определяет характер экстремума. Если производная второго порядка больше нуля, то в точке достигается строгий локальный минимум, если же она меньше нуля, то в точке достигается строгий локальный максимум.