3. Дифференциальное исчисление функций одного переменного

3.1. Определение производной

Рассмотрим функцию , определенную в окрестности некоторой точки . Разность будем называть приращением аргумента в точке , а разность - приращением функции в точке . Здесь предполагается, что принадлежит окрестности .

Определение. Если для функции , определенной в окрестности точки , существует предел отношения приращения функции к приращению аргумента

,

то этот предел называется производной функции в точке .

Производная обозначается обычно , либо . Если принять , то формальное определение производной принимает вид

= .

Операция нахождения производной называется дифференцированием.

3.2. Дифференциал функции

Определение. Функция , определенная в окрестности точки , называется дифференцируемой в этой точке, если приращение функции , где , представимо в виде

.

(x₀)– постоянная (для данной точки ); – функция, бесконечно малая относительно , т.е. при .

Линейное относительно слагаемое разложения называется дифференциалом функции в точке :

= .

Теорема (о дифференцируемости функции одной переменной). Функция дифференцируема в точке в том и только в том случае, когда имеет в этой точке производную. При этом A = .

Приращение независимой переменной x назовем дифференциалом dx независимой переменной х.

Тогда выражение для дифференциала функции примет симметричный вид .

Теорема (о связи дифференцируемости функции с непрерывностью). Если функция дифференцируема в точке, то она в этой точке непрерывна.

Обратное утверждение, вообще говоря, неверно: из того, что функция непрерывна в общем случае не следует, что она дифференцируема. Дифференцируемость является более сильным свойством, чем непрерывность.

3.3. Геометрический смысл производной и дифференциала

Производная функции – это угловой коэффициент касательной к графику функции в соответствующей точке:

,

где – угол наклона касательной к оси Ox.

Уравнение касательной: .

3.4. Формулы дифференцирования (таблица производных)

1. 

2. .

3. .

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

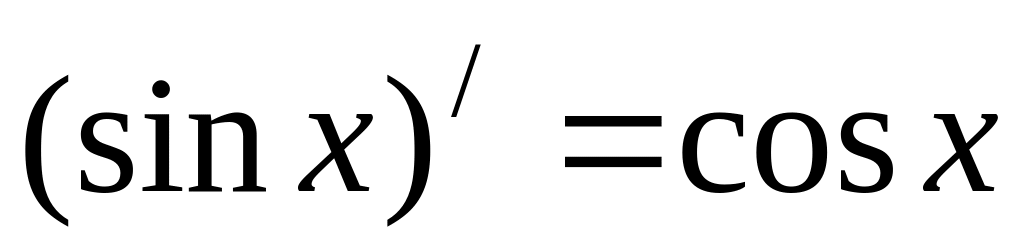
3.5. Правила дифференцирования

,

,

.

Теорема о дифференцировании обратной функции. Если функция непрерывна и строго монотонна в окрестности точки и имеет производную , то обратная функция имеет производную в точке , причем

.

Теорема о дифференцировании сложной функции. Если функция имеет производную в точке , функция имеет производную в точке , то сложная функция имеет производную в точке , причем

,

или, в краткой форме .

3.6. Производные и дифференциалы высших порядков

Рассмотрим функцию , имеющую производную в каждой точке окрестности точки . Тогда в окрестности определена новая функция – . При этом, если производная этой функции , в свою очередь, имеет производную в точке , то говорят, что исходная функция имеет в точке производную второго порядка («производная от производной»):

= .

Аналогично определяются производные более высоких порядков. В общем случае, производная некоторого -го порядка, где – натуральное число, определяется через производную на единицу меньшего порядка:

.

Пример 1. Рассмотрим показательную функцию

.

Производная функции

.

Производная второго порядка

.

Нетрудно видеть, что в общем случае

.

Пример 2. , , ,

.