3.13. Исследование функции и построение графика

1-шаг. Ищется область определения, область непрерывности и точки разрыва функции.

2-ой шаг. Функция исследуется на наличие наклонных и вертикальных асимптот.

3-ий шаг. С помощью производной первого порядка выявляются интервалы монотонности и точки локального экстремума функции.

4-ый шаг. С помощью производной второго порядка выявляются интервалы выпуклости функции, а также точки перегиба.

5-ый шаг. Стоится график.

Замечание. Описанные этапы 1–4 исследования позволяют качественно оценить поведение функции. Для более точного построения графика обычно ищут точки пересечения графика с осями, исследуют функцию на четность-нечетность, периодичность, выявляют интервалы, на которых функция сохраняет знак.

Задача. Исследовать функцию

и построить график.

Решение. Будем действовать в соответствии с приведенной выше схемой.

1-ый шаг. Функция определена и непрерывна на всей числовой прямой, кроме точки . В точке функция терпит разрыв.

2-ой шаг. Исследуем функцию на наличие асимптот.

2-ой шаг, пункт А. Зададимся вопросом, есть ли у функции наклонные асимптоты.

Исследуем функцию при стремлении переменного в . Вычислим предел , применив дважды правило Лопиталя:

=

.

Следовательно, функция не имеет асимптоты при .

Исследуем функцию при стремлении переменного в . Вычислим предел :

как предел отношения бесконечно малой к бесконечно большой.

Вычислим предел при найденном :

.

И здесь мы имеем дело с пределом отношения бесконечно малой к бесконечно большой.

Таким образом, при функция имеет асимптоту. Ее уравнение

.

Асимптота совпадает с осью переменного .

2-ой шаг, пункт Б. Исследуем функцию на наличие вертикальных асимптот. Функция имеет единственную точку разрыва, следовательно, может иметь разве что одну вертикальную асимптоту, определяемую этим разрывом. Рассмотрим поведение функции слева и справа от точки разрыва , вычислив односторонние пределы:

,

.

Здесь в обоих случаях мы имеем дело с отношением ограниченной положительной величины к бесконечно малой. Слева от точки разность является бесконечно малой отрицательной, справа от точки эта разность бесконечно мала и положительна. Полученные предельные соотношения указывают на наличие вертикальной асимптоты. Ее уравнение

.

3-ий шаг. Найдем производную

.

Производная обращается в нуль в точке . Точка - критическая точка (первого рода) функции. Для выявления интервалов монотонности функции заполним таблицу:

		2		3
	-	не существует	-	0	+
		точка разрыва		точка локального минимума
				1

Таким образом, на интервалах и функция строго убывает, а на интервале она строго возрастает . Точка является точкой строгого локального минимума, причем локальный минимум равен . Это значение указано в столбце, отвечающему .

4-ый шаг. Найдем производную второго порядка

.

Найдем нули производной второго порядка, или критические точки второго рода:

.

Уравнение не имеет действительных корней. Стало быть, у функции нет точек перегиба. Для выявления интервалов выпуклости и интервалов вогнутости заполним таблицу:

	–	не существует	+
		точка разрыва

Таким образом, функция вогнута на интервале и выпукла на интервале .

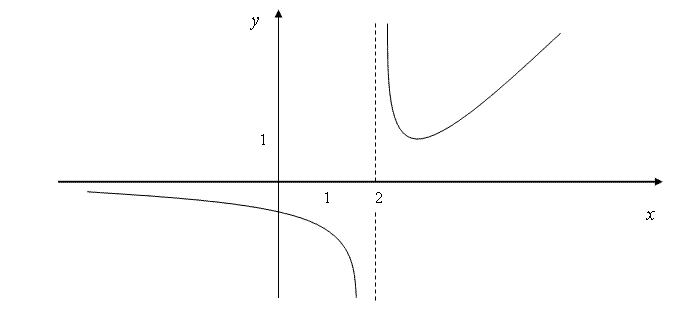
5-ый шаг. Построим график.