79. Сущность проблемы индуктивности в микроэлектронике. Реализация индуктивности с помощью аэ. Реализация активных фильтров (аф).

Реализация активных фильтров

Электрическим фильтром называется устройство для передачи электрических сигналов, пропускающее токи в определенной области частот и препятствующее их прохождению вне этой области. В радиотехнике и электронике электрические фильтры подразделяют на пассивные и активные. Схемы пассивных фильтров содержат только пассивные элементы: резисторы, конденсаторы и катушки индуктивности.

В схемы активных фильтров помимо указанных элементов входят такие активные изделия, как транзисторы или интегральные микросхемы. Фильтрующие свойства устройства определяются его амплитудно-частотной характеристикой, которой называется зависимость коэффициента усиления этого устройства от частоты сигнала. В некоторой области частот, которая называется полосой пропускания или полосой прозрачности, электрические колебания передаются фильтром с входа на выход практически без ослабления. Вне полосы прозрачности расположена полоса затухания или задерживания, в пределах которой частотные составляющие сигнала ослабляются. Между полосой прозрачности и полосой задерживания находится частота, называемая граничной. В связи с тем что существует плавный переход между полосой прозрачности и полосой затухания, граничной обычно считается частота, на которой ослабление сигнала оказывается равным -3 дБ - то есть по напряжению в √2 раз меньше, чем в полосе прозрачности.

С ростом порядка фильтра его фильтрующие свойства улучшаются. На одном ОУ достаточно просто реализуется фильтр второго порядка. Для реализации фильтров нижних частот, высших частот и полосовых фильтров широкое применение нашла схема фильтра второго порядка Саллена-Ки. На рис. 17 приведен ее вариант для ФНЧ. Отрицательная обратная связь, сформированная с помощью делителя напряжения R3, ( – 1)R3, обеспечивает коэффициент усиления, равный . Положительная обратная связь обусловлена наличием конденсатора С2. Передаточная функция фильтра имеет вид:

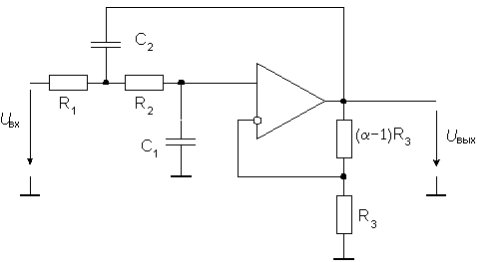
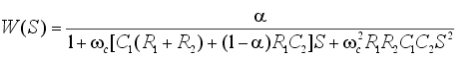
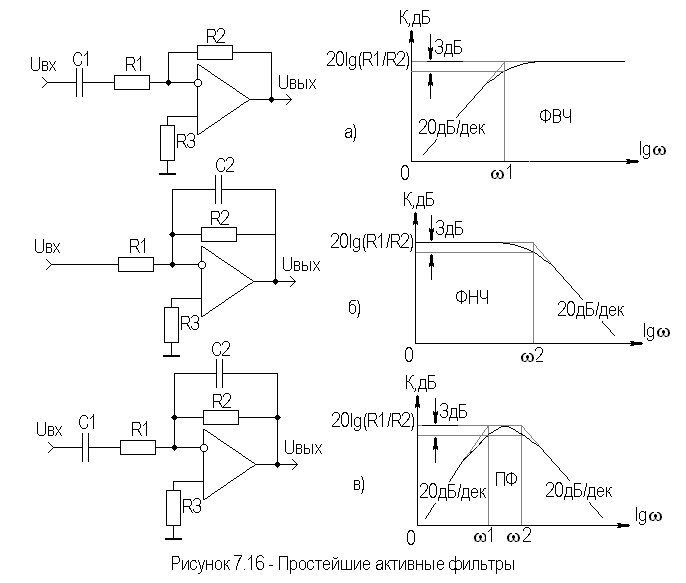
Разработано несколько конфигураций активных фильтров. Три основных из них:

1. С неограниченным коэффициентом усиления и много кратной обратной связью

2. С управляемым напряжением источником напряжения

3. С переменным состоянием

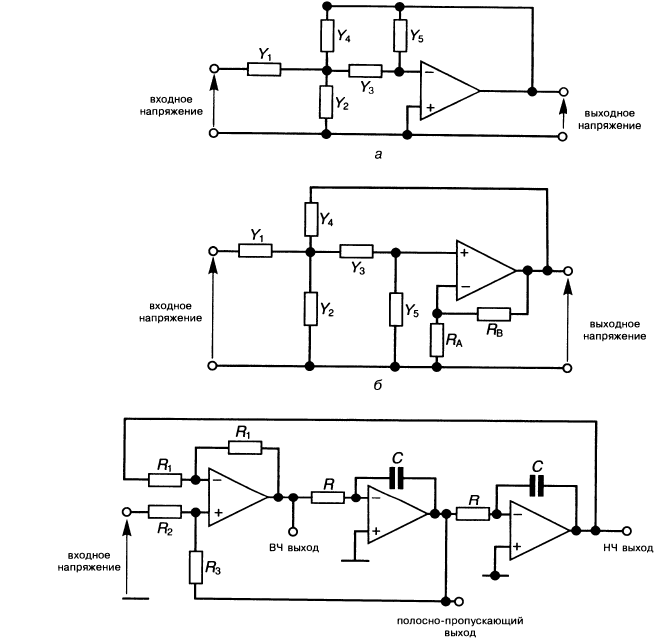
Схемы этих 3 фильтров представлены на рисунке. Следует заметить, что фильтр с переменным состоянием имеет 3 выхода: низкочастотный, высокочастотный и полосно-пропускающий.

80. Методы синтеза аф и их сравнительная оценка. Аппроксимация нормированной ачх фнч. Преобразование ачх фнч в ачх фвч и в ачх полосовых фильтров пф.

Первым этапом синтеза всякого фильтра является задание передаточной функции (в операторной или комплексной форме), которая отвечает условиям практической реализуемости и одновременно обеспечивает получение необходимой АЧХ или ФЧХ (но не обеих) фильтра. Этот этап называют аппроксимацией характеристик фильтра.

Операторная функция представляет собой отношение полиномов:

K(p)=A(p)/B(p),

и однозначно определяется нулями и полюсами. Простейший полином числителя - константа. Число полюсов функции (а в активных фильтрах на ОУ число полюсов обычно равно числу конденсаторов в цепях, формирующих АЧХ) определяет порядок фильтра. Порядок фильтра указывает на скорость спада его АЧХ, которая для первого порядка составляет 20дБ/дек, для второго - 40дБ/дек, для третьего - 60дБ/дек и д.д.

Задачу аппроксимации решают для ФНЧ, затем с помощью метода инверсии частоты полученную зависимость используют для других типов фильтров. В большинстве случаев задают АЧХ, принимая нормированный коэффициент передачи:

,

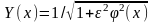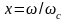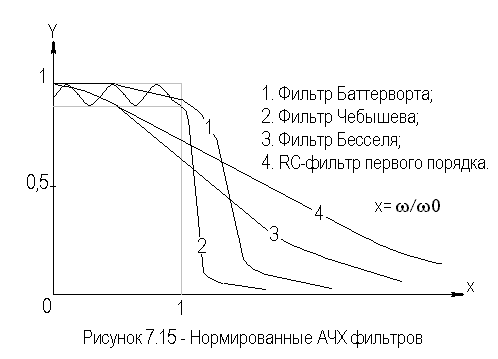
где (х) - функция фильтрации; - нормированная частота; 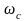- частота среза фильтра;  - допустимое отклонение в полосе пропускания.

В зависимости от того, какая функция принимается в качестве (х) различают фильтры (начиная со второго порядка) Баттерворта, Чебышева, Бесселя и др. На рисунке 7.15 приведены их сравнительные характеристики.

Фильтр Баттерворта (функция Батерворта) описывает АЧХ с максимально плоской частью в полосе пропускания и относительно небольшой скоростью спада. АЧХ такого ФНЧ может быть представлена в следующем виде:

,

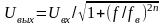где n - порядок фильтра.

Фильтр Чебышева (функция Чебышева) описывает АЧХ с определенной неравномерностью в полосе пропускания, но не большей скоростью спада.

Фильтр Бесселя характеризуется линейной ФЧХ, в результате чего сигналы, частоты которых лежат в полосе пропускания, проходят через фильтр без искажений. В частности, фильтры Бесселя не дают выбросов при обработке колебаний прямоугольной формы.

Помимо перечисленных аппроксимаций АЧХ активных фильтров известны и другие, например, обратного фильтра Чебышева, фильтра Золотарева и т.д. Заметим, что схемы активных фильтров не изменяются в зависимости от типа аппроксимации АЧХ, а изменяются соотношения между номиналами их элементов.

Переход от ФНЧ к ФВЧ, как видно из рисунков, осуществляется заменой резисторов на конденсаторы, и наоборот.

Либо возможно построение активного универсального фильтра (ФНЧ, ФВЧ и ПФ), вариант схемы которого приведен на рисунке 7.19.

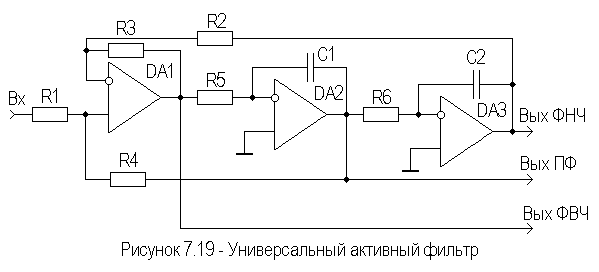
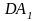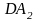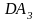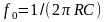В его состав входят сумматор на ОУ и два ФНЧ первого порядка на ОУ и , которые включены последовательно. Если , то частота сопряжения . ЛАЧХ имеет наклон асимптот порядка 40дБ/дек. Универсальный активный фильтр имеет хорошую стабильность параметров и высокую добротность (до 100). В серийных ИМС довольно часто используется подобный принцип построения фильтров.