62.Условный экстремум. Необходимый и достаточный признаки существования.

Опр Точка 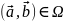– точка лок усл экстремума ф-ии 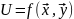при условии 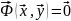, если сущ точки 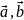, такая, что для 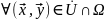выполнено хотя бы 1 из след нер-в:

1)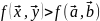 – строгий усл мин

2)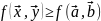 - усл мин

3)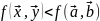 - строгий усл мах

4)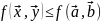 - усл мах

Т. (необх пр-к сущ-ния) Для того, чтобы точка 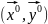была т. усл экстр ф-ии при ур-ниях связи необх чтобы её коoрд 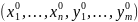при некот знач 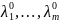удовл сис-ме уравнений:

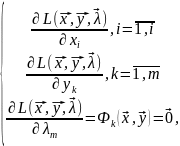
Т. (дост пр-к сущ-ния) Пусть ф-ии и имеют непрер частн произв 2го порядка в окр-сти точки стационарной для ф-ии Лагранжа при и в этой точке Якобиан (опред м-цы Якоби) отличен от 0, тогда наличие усл экстр для ф-ии определяется положит(для мин) или отриц(для мах) определённостью 2го диф-ла ф-ии Лагранжа при

63.Основные понятия числовых рядов.

Опр.Числ. ряд – посл-ть конечных сумм спец вида 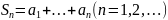постр по к-либо числ посл-ти

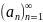
Осн.понятия:

1)общий член 2)частичная сумма 3)остаток 4)отрезок 5)знакопост 6)знакоположит/знакоотриц 7)знакопеременный

64.Простейшие операции над рядами.

Т.(об умножении членов ряда на число).Если ряд ∑ak сх и λ-число, то ряд ∑λak сх и след рав-во ∑λak=λ∑ak.

Т.(о почленном сложении рядов). Если ряды ∑ak и ∑bk сх, то ряд ∑(ak+bk) также сх и справедливо рав-во: ∑(ak+bk)= ∑ak+∑bk.

Т.(о группировке членов ряда).Пусть a₁+a₂+…-4P(числ ряд) и 1 n₁ n₂… возр посл-ть.Пусть далее образ нов ряд b₁+b₂+…, где b₁=a₁+…+a_n, b₂=a_n1+1+…+a_n2,…Тогда, если исод ряд ∑ak сход, то нов ряд ∑bj тож сх-ся и их суммы равны.

Т.Любая перестановка конечного числа членов ряда не нарушает его свойств сходимости и не нарушает его сумму.

65. Критерий Коши и другие критерии сходимости для числовых рядов

Т. 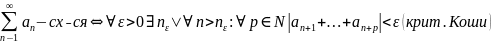, т.е любой отрезок ряда может быть сделан сколь угодно малым, начиная с некоторого номера.

Т.(критерий сх-ти ряда в терминах остатов)Сх-ть ряда ∑ak равносильна сх-ти любого его остатка. В случае сх-ти ряда посл-ть (r_n) суммы остатков стремится к 0.

Т.(критерий сх-ти ряда с неотриц членами)Сх-ть числ ряда с неотриц членами равнос ограниченности сверху посл-ти его частных сумм.

66. Признаки сравнения для знакоположительных рядов.

Т.(Мажорантный признак сравнения). Пусть ∑ak и ∑bk ряды с неотриц членами и ak=O(bk) при k→∞, тогда : 1)Если ряд ∑bk сх-ся, то ряд ∑ak также сх-ся; 2) Если ряд ∑ak расх-ся, то ряд ∑bk также расх-ся.

Т.(признак сравнения в предельной форме).Пусть ∑bk и ∑ak-знакополож ряды и существует lim ak/bk=Lє[0;+∞), тогда: 1)При 0<L<+∞ ряды ∑bk и ∑ak оба сх-ся или расх; 2)При L=0 из сх ниж ряда из ∑bk вытекает сх-ть ряда ∑ak; 3)При L=+∞ из расход-ти верхнего ряда ∑ak вытекает расх-ть нижнего ряда ∑bk.

Т.(признак сравнения отношения).Пусть сумма ∑ak и ∑bk-знакоположит ряды и для всех вы прав-во: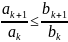 , тогда: 1)∑bk сх, тогда ∑ak сх; 2)∑ak расх, тогда ∑bk расх.

67. Интегральный признак сходимости для знакоположительных рядов. Следствия. Т.(Интеграл призн Маклорена-Коши).Пусть f:[1;+∞)→R-положит убывающ ф-ия, тогда сходимость числового ряда ∑f(x) равносильна существованию конечного lim f(x) первообразной F(x) для ф-ии f(x). Сл.Для гармонического ряда ∑ имеем f(x)=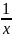 . 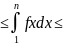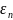Её первообразная F(x)=ln x→+∞, тогда ряд ∑ расх-ся.Из отношения S_n-f(1) S_n-1 при f(x)= вытекает приближ знач для частных сумм гармонического ряда ∑ : Более точная ф-ла: , →0, c=lim(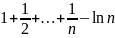 ) наз постоянной Эйлера(с=0,577…) 68. Признаки Коши и Даламбера

Т.(Пр-к Коши(с корнем)). Пусть ∑ak-ряд с неотриц членами, для кот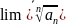 =q, тогда: 1)при q<1 ряд сх-ся; 2)при q>1 ряд расх-ся; 3)при q=1 необх дополн исслед ряда.

Т.(Пр-к Даламбера).Пусть для знакаположительного ряда ∑ak сущ-ет lim =D, тогда: 1)при D<1 ряд сх-ся; 2)при D>1 ряд расх-ся; 3)при D=1 необх дополн исслед ряда.