
- •1.Первообразная, неопределённый интеграл и их свойства.
- •13.Интегрирование дифференциальных биномов
- •14. Понятие определённого интеграла Римана. Необходимое условие интегрируемости.
- •29.Открытые и замкнутые множества в r2
- •36. Основные классы кривых
- •53.Достаточное условие дифференцируемости отображения в точке.
- •54. Производная по направлению.
- •55.Теорема Лагранжа оконечных приращениях
- •57.Локальный экстремум функций векторного аргумента. Необходимое условие.
- •58. Достаточное условие локального экстремума ф-ции вект. Аргумента (общий случай)
- •59. Теорема о существовании локального экстремума для функций двух переменных.
- •62.Условный экстремум. Необходимый и достаточный признаки существования.
- •63.Основные понятия числовых рядов.
- •64.Простейшие операции над рядами.
- •65. Критерий Коши и другие критерии сходимости для числовых рядов
- •66. Признаки сравнения для знакоположительных рядов.
- •69. Признаки Куммера и Раабе.
- •70. Признаки Бертрана и Гаусса.
53.Достаточное условие дифференцируемости отображения в точке.
Т.
Если частная производная всех корд
ф-ий
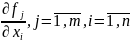 ,
ceo
в окр-сти т.
и непр-на в самой этой точке, то отобр
f
диф-мо в т.
,
ceo
в окр-сти т.
и непр-на в самой этой точке, то отобр
f
диф-мо в т.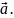
54. Производная по направлению.
Опр.
Пусть Е – открытое мн-во в Rn
и
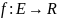 – скал ф-ия. Пусть далее
– скал ф-ия. Пусть далее
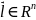 – некот единичный в-р, тогда производная
по направлению
– некот единичный в-р, тогда производная
по направлению
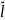 наз число
наз число
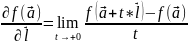 ,
если lim
сущ-ет и конечен.
,
если lim
сущ-ет и конечен.
Т.
Пусть
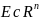 открытое мн-во и скал ф-ия
диф-ма в т.
открытое мн-во и скал ф-ия
диф-ма в т.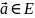 ,
тогда в этой точке сущ производная по
любому направл.
,
тогда в этой точке сущ производная по
любому направл.
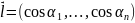 и верно рав-во
и верно рав-во

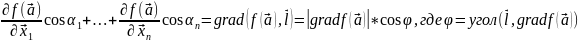
55.Теорема Лагранжа оконечных приращениях
Опр.
Отрезком в Rn
с началом в точке
и концом в т.
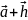 наз-ся мн-во
наз-ся мн-во
 а
интервалом:
а
интервалом:

Т.Пусть
скал ф-ия
,
,
непрерывна на отрезке
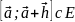 и
диф-ма во всех точках интервала
и
диф-ма во всех точках интервала
 .
Тогда сущ-ет такая т.
.
Тогда сущ-ет такая т.
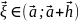 ,
что
,
что
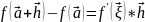
56. Диф-лы высших порядков. Ф-ла Тейлора
Опр
Диф-лом
второго порядка от скал ф-ции
в т.
 на в-ре
на в-ре
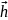 наз-ся диф-ал от 1-ого диф-ла:
наз-ся диф-ал от 1-ого диф-ла:
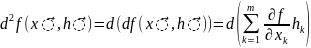
Теор
Если все
частн. произв. 1-го порядка скал. ф-ции
диф-мы в т.
,
то
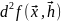 ,
где
,
где
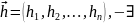 и явл-ся квадратичной формой от перем.
и явл-ся квадратичной формой от перем.
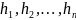
Опр
Формой
степени
 наз-ся целая рац. ф-ция однородная
степени p
от этих перем.
наз-ся целая рац. ф-ция однородная
степени p
от этих перем.
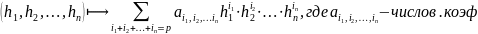
Опр
Диф-лом
порядка
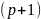 от ф-ции
в т.
на в-ре
наз-ся диф-ал от диф-ала пор. р:
от ф-ции
в т.
на в-ре
наз-ся диф-ал от диф-ала пор. р:
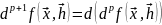
Теор
Если все
част. произв. порядка р ф-ции
,
диф-мой в т.
,
то
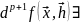 b
явл-ся формой степени (р+1) от прем.
b
явл-ся формой степени (р+1) от прем.
Ф-ла Тейлора для скал. ф-ции 2-ух перем имеет вид
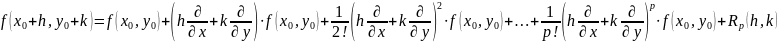
57.Локальный экстремум функций векторного аргумента. Необходимое условие.
Опр.
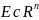 – область, т.
– область, т.
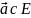 наз-ся точкой внутрен локального
экстремума скал ф-ии
наз-ся точкой внутрен локального
экстремума скал ф-ии
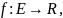 если сущ её проколот окрестность
если сущ её проколот окрестность
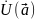 ,
в кот выполнено хотя б одно из след
нер-в:
,
в кот выполнено хотя б одно из след
нер-в:
1) (строгий лок мах)
(строгий лок мах)
2)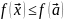 (лок мах)
(лок мах)
3)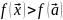 (строгий
лок мин)
(строгий
лок мин)
4)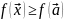 (лок
мин)
(лок
мин)
Т.
(необх усл лок экстр диф-ой ф-ии) Пусть
скал ф-ия
диф-ма в т.
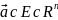 и имеет в этой точке лок экстр, тогда в
этой точке все частн произв 1го порядка
равны нулю
и имеет в этой точке лок экстр, тогда в
этой точке все частн произв 1го порядка
равны нулю
Опр. Стационарная точка – точка, в кот ф-ия диф-ма и все частные производные равны 0
58. Достаточное условие локального экстремума ф-ции вект. Аргумента (общий случай)
Теор
Пусть
– стац. т. скал. ф-ции
и в этой т.
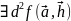 .
Если кв
форма
.
Если кв
форма
 :
:
положит. опред, то имеет в т. стр. лок. мин.
отриц. опред, то имеет в т. стр. лок. макс.
неопред., то не имеет экстр. в т.
59. Теорема о существовании локального экстремума для функций двух переменных.
Теор.Пусть (a;b)-стац точка диф скал ф-ии r=f(x,y). Пусть сущ производ 2ого порядка ф-ия диф на [a;b].Пусть A=∂2f(a,b)/∂x2, B=∂2f(a,b)/∂x∂y, C=∂2f(a,b)/∂y2. Тогда:1)если A>0, AC-B2>0, то в т.(a,b) ф-ия имеет строгий лок максимум; 2)если A<0, AC-B2>0, то в т.(a,b) ф-ия имеет строгий лок минимум; 3)если AC-B2<0, то в т.(a,b) ф-ия не имеет экстремума; 4)если A=0 или AC-B2=0, то необходимо дополнительные исследования (могут реализ все случаи).
60.
Теорема о существовании, единственности
и непрерывности неявной функции
скалярного аргумента. Теор.
Предположим выполняется след
условия:1)F:E→R,
EcR2(т.е.
F(x,y))
непрер в прямоугольнике: {(x,y)||x-x0|
∆,
|y-y0|
∆’}cE
с центром в точке (x0,y0);
2)Вы прав-во F(x0,y0)=0;
3)При каждом xє[x0-∆,x0+∆]
ф-ия F(x,y)
строго монотонна по переменной y.
Тогда в некоторой окр-ти (x0-δ;x0+δ)
существует единственная ф-ия y=y(x),
такая что
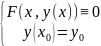 .
.
61.
Дифференцируемость неявной функции
скалярного аргумента. Теоремы о неявных
функциях векторного аргумента.
Т.Пусть
выполняются условия: 1)ф-ия F:E→R,
EcR2(т.е.
F(x,y))
имеет непрерывн частную производ 1ого
порядка в нек окр-ти т.(x0,y0)єE;
2)F(x0,y0)=0;
3)
 (x0,y0)
(x0,y0)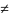 0;
Тогда в некоторой окр-ти (x0-δ;x0+δ)
существует единственная дифф-ая ф-ия
y=y(x)
для которой y0=y(x0)
0;
Тогда в некоторой окр-ти (x0-δ;x0+δ)
существует единственная дифф-ая ф-ия
y=y(x)
для которой y0=y(x0)
 ,
y’(x)=-
,
y’(x)=-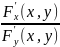 .
Т.Пусть,
предположим что: 1)F(
,y)
непрерыв в (n+1)-мерном
параллелепипеде: П={|x1-
.
Т.Пусть,
предположим что: 1)F(
,y)
непрерыв в (n+1)-мерном
параллелепипеде: П={|x1-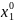 |
∆1,…,
|xn-
|
∆1,…,
|xn-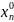 |
∆n,|y-y0|
∆’}
в центре с т.(
|
∆n,|y-y0|
∆’}
в центре с т.(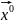 ,
,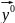 )=(
)=(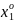 ,…,
,…,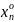 ,yo);
2)F(
,y0)=0;
3)При каждом
єП
ф-ия F(
,y)
строго монотонна по y.
Тогда в некотор окр т.x0
единств непр ф-ия y=y(
),
такая что y0=y(
)
и F(
,y(
))
,yo);
2)F(
,y0)=0;
3)При каждом
єП
ф-ия F(
,y)
строго монотонна по y.
Тогда в некотор окр т.x0
единств непр ф-ия y=y(
),
такая что y0=y(
)
и F(
,y(
))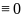 .
Т.Предположим
вып усл: 1)F(
,y)
непрерыв частн производ 1ого порядка
в некотор окр-ти (
,y0);
2) F(
,y0)=0;
3)
(
,y0)
0.
Тогда сущ такая окр-ть
котор ур-ние F(
,y)=0
опред единств дифф ф-ию y=y(
),
такую что y0=y(
),
F(
,y(
))
,
.
Т.Предположим
вып усл: 1)F(
,y)
непрерыв частн производ 1ого порядка
в некотор окр-ти (
,y0);
2) F(
,y0)=0;
3)
(
,y0)
0.
Тогда сущ такая окр-ть
котор ур-ние F(
,y)=0
опред единств дифф ф-ию y=y(
),
такую что y0=y(
),
F(
,y(
))
,
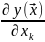 =-
=- .
.
