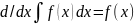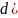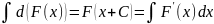- •1.Первообразная, неопределённый интеграл и их свойства.
- •13.Интегрирование дифференциальных биномов
- •14. Понятие определённого интеграла Римана. Необходимое условие интегрируемости.
- •29.Открытые и замкнутые множества в r2
- •36. Основные классы кривых
- •53.Достаточное условие дифференцируемости отображения в точке.
- •54. Производная по направлению.
- •55.Теорема Лагранжа оконечных приращениях
- •57.Локальный экстремум функций векторного аргумента. Необходимое условие.
- •58. Достаточное условие локального экстремума ф-ции вект. Аргумента (общий случай)
- •59. Теорема о существовании локального экстремума для функций двух переменных.
- •62.Условный экстремум. Необходимый и достаточный признаки существования.
- •63.Основные понятия числовых рядов.
- •64.Простейшие операции над рядами.
- •65. Критерий Коши и другие критерии сходимости для числовых рядов
- •66. Признаки сравнения для знакоположительных рядов.
- •69. Признаки Куммера и Раабе.
- •70. Признаки Бертрана и Гаусса.
1.Первообразная, неопределённый интеграл и их свойства.
Опр F(x) – первообр для f(x) на некот промежутке, если на этом промеж F(x) – дифф и F’(x)=f(x)
Св-ва первообр:
1)Если F(x) – первообр для f, то F(x)+C – также первообр
2)Если F(x) – первообр для f, x€X, то любая др первообр для f на том же промеж будет F(x)+C
3)Разность между V 2мя первообр для f(x) на промеж = С
Опр
Неопр инт-л
от f
на некот промеж наз-ся мн-во всех первообр
для f
на этом промеж, и обозн
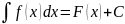 , где F(x)
– любая первообр для f,
C=const
, где F(x)
– любая первообр для f,
C=const
Св-ва неопр инт-ла:
2.Таблица основных интегралов
1)∫A(x)dx=Ax+C; 2)∫xαdx=((xα+1)/(α+1))+C; 3)∫dx/x=ln|x|+C; 4)∫axdx=ax/lna; 5)∫sinxdx=-cosx+C; 6)∫cosxdx=sinx+C; 7)∫dx/cos2x=tgx+C; 8)∫dx/sin2x=-ctgx+C; 9)∫shxdx=chx+C; 10)∫chxdx=shxdx+C; 11)∫dx/ch2x=thx+C; 12) ∫dx/sh2x=-cthx+C; 13)∫dx/(x2+1)=arctgx+C; 14)∫dx/(x2-a2)=(1/2a)*ln|(x-a)/(x+a)|;
3. Методы разложения и внесения под знак дифференциала.
Метод разложения
Интеграл от лин комбин конечного числа инт ф-ий равен той же комбинации инт-лов от инт ф-ий
Const множитель можно выносить за знак диф-ла
Метов внесения под знак диф-ла
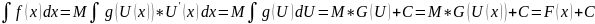
4.Замена переменной в неопределённом интеграле.
Т.
Пусть x€[a;b]
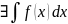 и отобр
и отобр
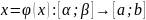 – диф-ема и биективна. Тогда
– диф-ема и биективна. Тогда
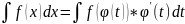 ,
где
,
где
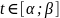
5.Метод интегрирования по частям.
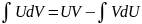
6.Разложение рациональной функции на простые дроби.
Первообразная
любой рац ф-ии
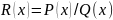 выражается через рац ф-ии, а также ln
и arctg.
Рац часть первообразной, будучи приведена
к общему знаменателю, должна в качестве
такового иметь произведение всех
сомножителей, на которые раскладывается
многочлен Q(x),
только с кратностями, на единицу
меньшими, чем кратность их вхождения
в разложение Q(x).
выражается через рац ф-ии, а также ln
и arctg.
Рац часть первообразной, будучи приведена
к общему знаменателю, должна в качестве
такового иметь произведение всех
сомножителей, на которые раскладывается
многочлен Q(x),
только с кратностями, на единицу
меньшими, чем кратность их вхождения
в разложение Q(x).
7.Интегрирование рациональных функций.
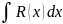 ,
где
,
где
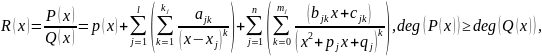
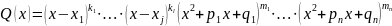
Первообразная
любой рациональой функции
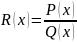 выражается через рациональные функции,
а также трнсцендентные функции
выражается через рациональные функции,
а также трнсцендентные функции
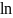 и
и
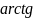 .
.
8.Метод Остроградского
метод
выделения рациональной части
неопределенного интеграла от рациональной
дроби,
знаменатель которой — многочлен степени
n с кратными корнями, а числитель —
многочлен степени m 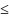 n-1.
Согласно этому методу,
n-1.
Согласно этому методу,
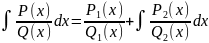 ,
где
многочлены Q1,
Q2,
P1,
P2 имеют
степени соответственно n1,
n2,
m1,
m2,
такие что n1 +
n2 =
n, m1
n1 —
1, m2
n2 —
1 и
многочлен Q2(x)
не имеет кратных корней. Таким образом,
Q1(x)
является наибольшим общим делителем
многочленов Q(x) и
,
где
многочлены Q1,
Q2,
P1,
P2 имеют
степени соответственно n1,
n2,
m1,
m2,
такие что n1 +
n2 =
n, m1
n1 —
1, m2
n2 —
1 и
многочлен Q2(x)
не имеет кратных корней. Таким образом,
Q1(x)
является наибольшим общим делителем
многочленов Q(x) и 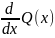 ,
следовательно, его можно найти,
используя алгоритм
Евклида.
Из этого равенства, дифференцируя,
получаем тождество, которое позволяет
найти явное выражение многочленов
P1(x)
и P2(x).
,
следовательно, его можно найти,
используя алгоритм
Евклида.
Из этого равенства, дифференцируя,
получаем тождество, которое позволяет
найти явное выражение многочленов
P1(x)
и P2(x).
9.Интегрирование некоторых тригонометрических выражений.
a)
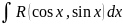 :
:
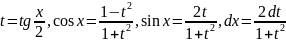
б)
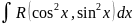 или
или
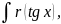 где
где
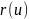 – рациональная
функция:
– рациональная
функция:
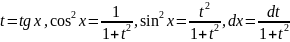
в)
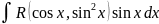 или
или
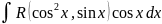
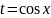 или
или
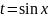 :
:
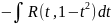 и
и
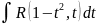
10.Интегрирование дробно-линейных иррациональностей.
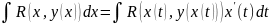
Если
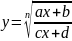 ,
то
,
то
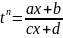 ,
,
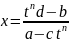 ,
y=t.
,
y=t.
11.Подстановки Эйлера
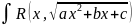
a>0:
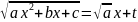
c>0:
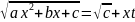
a<0, c<0, D>0, x1<x<x2:
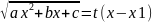
12.Выделение алгебраической части интеграла
Ф-ия наз алгебраической, если в D(f) она обладает тождеству вида:pk(x)[f(x)]k+ pk-1(x)[f(x)]k-1+…+ p1(x)f(x)+ p0(x)=0, где n>=1, nєZ, pk, pk-1,…,p0,-некоторые многочлены, Pk(x)≠0.
Подинтегральную
ф-ию
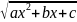 алгебр преобраз всегда можно представить
в виде суммы:R1(x)/
+R2(x),
где R1(x),
R2(x)
–рац ф-ии.∫ R(x,
)
можно привести к инт-лу вида: ∫R1(x)/
dx.
Разложив рац R1(x)
на сумму многочленов pr(x)
элем-ных дробей приходим к инт-лам след
3х видов:а)∫Pr(x)/
dx;
б)∫1/((x-α)k
)dx,
kєN;
в)(Mx+N)/((x2+px+q)m
)dx,
mєN.
алгебр преобраз всегда можно представить
в виде суммы:R1(x)/
+R2(x),
где R1(x),
R2(x)
–рац ф-ии.∫ R(x,
)
можно привести к инт-лу вида: ∫R1(x)/
dx.
Разложив рац R1(x)
на сумму многочленов pr(x)
элем-ных дробей приходим к инт-лам след
3х видов:а)∫Pr(x)/
dx;
б)∫1/((x-α)k
)dx,
kєN;
в)(Mx+N)/((x2+px+q)m
)dx,
mєN.