3.4 Решение уравнений методом итераций

Применим метод для решения уравнения вида:

Пусть [a, b] – промежуток локализации корня и .

Последовательность сходится к корню уравнения при условии на [a, b] (ε – корень уравнения ).

Условие окончания итераций:

f(t)=0, где

Приведение этого уравнения к виду, пригодному для метода итераций:

, где

1)

y=x

2)

y=x

y₌φ(x)

φ(x₀)

φ(x₁)

φ(x₁)

y₌φ(x)

x

x

φ(x₀)

x₂

x₁

x₀

x₁

x₂

x₀

- Строго монотонна

- Колеблющаяся

Результаты расчетов сведем в таблицу:

n
0	2.035	-
1	2.03915	4.15281*10-3

q=9.80489*10^-3

4. Вычисление интеграла I для линейной модели с сосредоточенными параметрами

При закон изменения температуры пластины ,

где

[с]- постоянная времени системы.

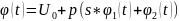
Требуется найти приближенное значение интеграла I с абсолютной погрешностью не более .

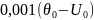Обозначим .

Абсолютная погрешность вычисления J не должна превышать

4.1. Вычисление интеграла I по формуле прямоугольников

, где

n- число делений [0, ]

–шаг интегрирования

– формула прямоугольника.

Оценка абсолютной погрешности :

,

Если требуется .

Так как искать сложно, для оценки погрешности используется правило Рунге:

если , то ,

где 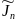- приближенное значение интеграла при числе разбиений n

– приближенное значение интеграла при числе разбиений 2n.

Результаты расчетов сведем в таблицу:

n
1	141.222	-
2	125.257	15.965
4	120.929	4.328
8	119.834	1.095
16	119.56	0.274

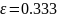
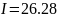
4.2. Вычисление интеграла по формулам трапеций

[с]- постоянная времени система.

n- число делений [0; ]

- шаг интегрирования

- формула трапеции.

Оценка абсолютной погрешности: , где .

Если требуется , то .

Так как считать сложно, для оценки погрешности используется правило Рунге:

Если , то

Результаты расчетов сведем в таблицу:

n
1	74.429	-
2	107.825	33.396
4	116.541	8.716
8	118.735	2.194
16	119.285	0.55