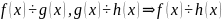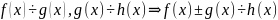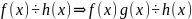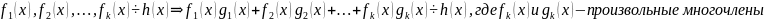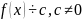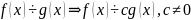- •16. Матрица линейного преобразования. Связь между координатами вектора и его образа.
- •17. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при смене базиса.
- •18. Связь между матрицами линейного преобразования в разных базисах. Подобные матрицы.
- •19. Операции над линейными пространствами.
- •20. Собственные значения и собственные векторы линейных преобразований. Порядок нахождения собственных векторов линейного пространства.
- •21. Определение эвклидового пространства. Примеры. Длина вектора и угол между векторами в эвклидовом пространстве.
- •22. Неравенство Коши-Буняковского в эвклидовом пространстве. Неравенство треугольника.
- •23. Ортогональность векторов. Процесс ортогонализации систем линейно независимых векторов. Ортонормированные базисы.
- •24. Ортогональные матрицы. Свойства ортогональных матриц.
- •26. Симметрические преобразования эвклидовых пространств.
- •27. Квадратические формы. Матрица квадратичной формы. Смена квадратичной формы при линейном преобразовании неизвестных.
- •29. Теорема о приведении симметричной матрицы к диагональному виду. Приведение квадратичной формы к главным осям.
- •31.Упрощение уравнений линий второго порядка на плоскости.
- •25. Ортогональные преобразования эвклидовых пространств.
- •28. Канонический вид квадратичной формы. Приведение квадратичной формы к каноническому виду методом Лагранжа. Закон инерции квадратичных форм.
- •2. Деление многочленов. Теорема о делении с остатком. Свойства делимости многочленов.
- •3. Наибольший общий делитель двух многочленов. Алгоритм Эвклида для нахождения наибольшего общего делителя
- •6. Понятие кратного корня многочлена. Производная многочлена. Связь между корнями многочлена и его производной.
- •7. Основная теорема алгебры и следствие из нее.
- •5. Корень многочлена. Теорема Безу. Схема Горнера деления многочлена на многочлен первой степени.
- •8. Рациональные корни многочлена с целыми коэффициентами.
- •9. Многочлены с действительными коэффициентами. Теорема про комплексные корни многочлена.
- •10. Границы действительных корней многочлена. Лемма о знаке старшего члена многочлена. Некоторые способы оценки корней многочленов.
- •15. Линейные преобразования линейных пространств. Примеры.
- •11. Система Штурма: определение и построение для заданного многочлена. Теорема Штурма. Локализация корней методом Штурма.
- •12. Приближенные методы вычисления корней многочленов. Метод половинного деления и метод Ньютона.
- •13. Определение линейного пространства. Примеры. Свойства линейного пространства.
- •14. Линейная зависимость и линейная независимость векторов. Размерность и базис линейного пространства.
2. Деление многочленов. Теорема о делении с остатком. Свойства делимости многочленов.
Многочлен
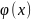 называется делителем
многочлена
называется делителем
многочлена
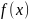 ,
если существует такой многочлен
,
если существует такой многочлен
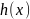 ,
что
,
что
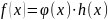 .
.
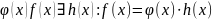
Теорема
о делении с остатком.
Для любых двух многочленов
и
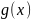 существуют
существуют
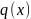 и
и
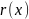 , такие что:
, такие что:
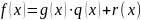 ,
при этом степень
строго меньше степени
.
Многочлены
и
определяются однозначно для
и
.
,
при этом степень
строго меньше степени
.
Многочлены
и
определяются однозначно для
и
.
Докажем
вторую часть теоремы:
Пусть существуют такие
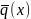 и
и
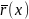 ,
для которых выполняется
,
для которых выполняется
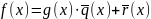 .
.
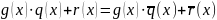
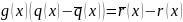

Тогда
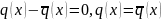
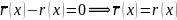
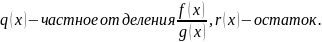
Свойства
делимости многочленов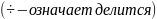 :
:
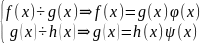
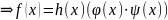
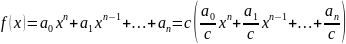
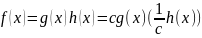
Многочлены и одновременно делятся друг на друга, когда
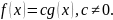
Всякий делитель одного из многочленов и
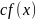 является делителем и другого многочлена.
является делителем и другого многочлена.
3. Наибольший общий делитель двух многочленов. Алгоритм Эвклида для нахождения наибольшего общего делителя
Многочлены и называются взаимно простыми, если их НОД равен единице.
Многочлен
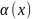 называется НОД
многочленов
и
, если он является общим делителем и
сам делится на любой другой общий
делитель.
называется НОД
многочленов
и
, если он является общим делителем и
сам делится на любой другой общий
делитель.
Алгоритм Эвклида:
НОД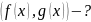
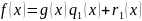
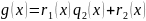
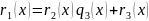
…..
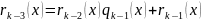
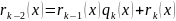
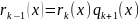
НОД
Доказательство (по определению):
(снизу вверх)
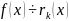
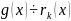
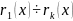
…
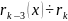
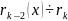
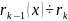
(сверху вниз)
Пусть
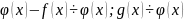
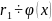
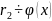
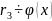
…
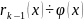
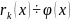
НОД многочленов определен лишь с точностью до многочленов нулевой степени.
6. Понятие кратного корня многочлена. Производная многочлена. Связь между корнями многочлена и его производной.
Корень многочлена имеет кратность К если f(x )/(f-c)k и не делится на (x +1)k+1, если К=1,то с-
простой корень. Многочлен f(x ) степени n называется многочленом n-1 степени.
_ f’(x )= n*A0x n-1+(n-1)A1x n-2+…+2A(n-2)x +A(n-1)
_f’’(x ) =(f’(x ))’ n-я производная
_f(n)(x )= n!A0
_f(n+1)(x )=0
Теорема: Если с является корнем кратности k многочлена f(x ) то при k>1 с является корнем кратности k-1, его производной f’(x ). Если k = 1, то число с не является корнем f’(x ).
7. Основная теорема алгебры и следствие из нее.
Основная теорема алгебры. Всякий многочлен с любыми числовыми коэффициентами имеет хотя бы один корень на множестве комплексных чисел.
Следствие.
Всякий многочлен степени
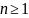 с любыми числовыми коэффициентами
имеет на множестве комплексных чисел
ровно
корней с учетом их кратности.
с любыми числовыми коэффициентами
имеет на множестве комплексных чисел
ровно
корней с учетом их кратности.
Доказательство:
по теореме алгебры
имеет хотя бы один корень
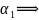 (по теореме Безу)
(по теореме Безу)
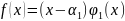 Пусть
Пусть
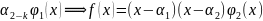
4. Неприводимые многочлены. Свойства неприводимых многочленов. Теоремы про разложение многочленов на неприводимые множители.
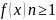 приводим
в числовой системе
приводим
в числовой системе
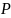 ,
если он может быть разложен в этой
системе в произведение двух множителей,
степени которых меньше
.
,
если он может быть разложен в этой
системе в произведение двух множителей,
степени которых меньше
.
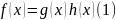
неприводим, если в любом разложении вида (1) один многочлен имеет степень 0, другой – 1.
Некоторые свойства неприводимых многочленов:
Всякий многочлен первой степени неприводим.
Если
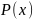 неприводим, то неприводимым будет и
неприводим, то неприводимым будет и
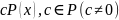
Если – произвольный многочлен, - неприводимый, то, либо
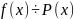 ,
либо они взаимно простые.
,
либо они взаимно простые.
Доказательство:
НОД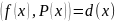
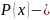 неприводим
неприводим
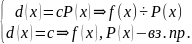
Теорема 1: Всякий многочлен степени , с коэффициентами из числового множества разлагается в произведение неприводимых множителей.
Доказательство:
Если
неприводим, то теорема доказана. Если
- приводим, то
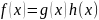 ,
если
и
– неприводимы,
то теорема доказана. Если хотя бы один
из них приводим, то раскладываем дальше
и т.д. за
шагов придем
к результату.
,
если
и
– неприводимы,
то теорема доказана. Если хотя бы один
из них приводим, то раскладываем дальше
и т.д. за
шагов придем
к результату.
Теорема
2: Всякий
многочлен разлагается на неприводимые
множители однозначно, с точностью до
множителей нулевой степени.
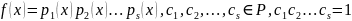
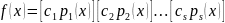
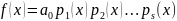
Если
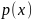 встречается
встречается
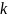 раз, то он называется -кратным множителем,
если он встречается один раз, то
называется простым множителем.
раз, то он называется -кратным множителем,
если он встречается один раз, то
называется простым множителем.
Пусть
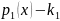 раз;
раз;
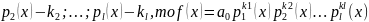 (2)
(2)
Если даны разложения многочленов вида (2), то НОД этих многочленов равен произведению множителей