Диференціальне числення фдз. Частинні прирости, похідні та диференціали.

Розглянемо функцію . Візьмемо довільну точку з області визначення функції і надамо аргументу приріст , залишаючи без зміни.

Функція отримала приріст , який називається частинним приростом функції по змінній .

Означення. Частинною похідною функції декількох змінних по одній із них називається границя відношення відповідного частинного приросту функції до приросту цієї змінної, коли останній прямує до нуля, якщо границя цього відношення існує.

Отже,

– частинна похідна функції по .

Інші позначення ; ; .

– частинна похідна функції по .

Інші позначення ; ; .

Вирази вигляду і називаються частинними диференціалами.

З означення частинної похідної по одній із змінних випливає, що при її знаходженні ми повинні усі інші змінні розглядати як сталі величини. Слід зазначити, що для частинних похідних справедливі усі теореми, властивості, аналогічні похідній функції однієї змінної (одного аргумента).

Приклад . Знайти частинні похідні функцій:

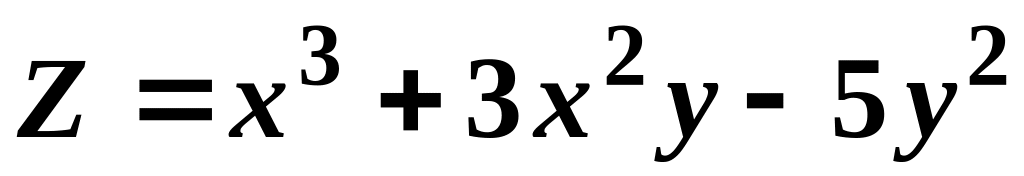
а)	б)
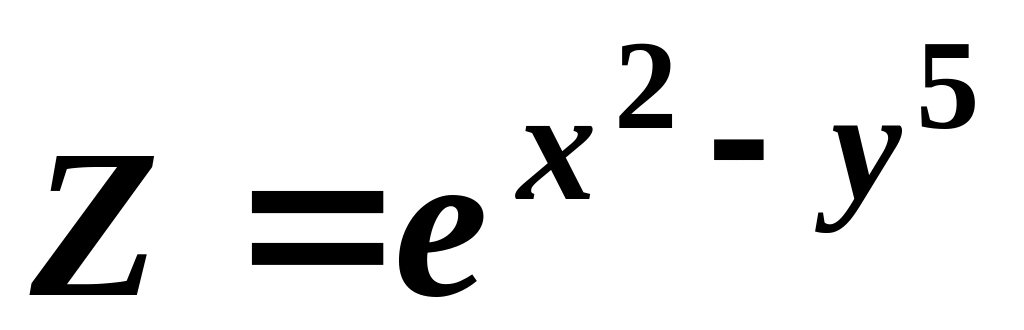
в) 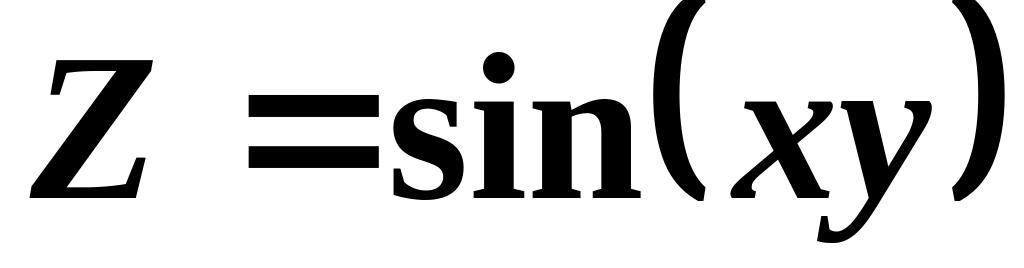;	г) .

Розв’язування. При знаходженні частинних похідних функції двох змінних застосовуються арифметичні теореми для диференційовних функцій, таблиця похідних основних елементарних функцій, теорема про похідну складеної функції однієї змінної.

а) ; .

б) ;

.

в) ; .

г) ;

.

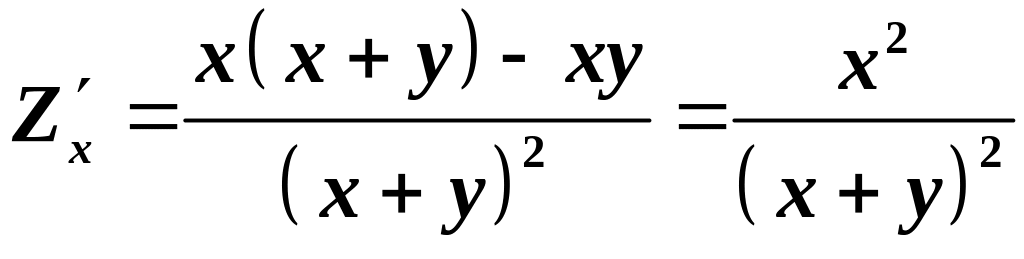Диференційовність функції двох змінних.

Функція називається диференційовною в точці , якщо її повний приріст у цій точці може бути поданим у вигляді:

,

де і – нескінченно малі величини при і .

Головна (лінійна відносно і ) частина повного приросту диференційовної функції , називається повним диференціалом цієї функції і позначається , тобто

, де і - диференціали незалежних змінних (аргументів), які співпадають з їх приростами.

Зауважимо, що на відміну від функції однієї змінної, для якої диференційовність еквівалентна існуванню похідної, для диференційовності ФДЗ необхідно не тільки існування, а ще й неперервність частинних похідних.

Приклад . Знайти частинні і повний диференціали функції у точці .

Розв’язування.

- неперервна; ; ;

- неперервна; ; ;

.

Похідна за напрямком.

Відзначимо, що 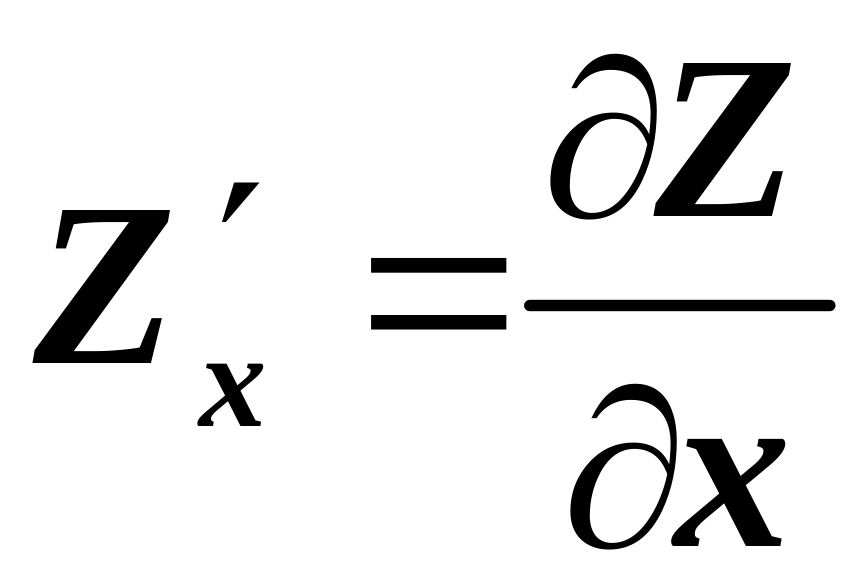є похідною функції у випадку, коли точка зміщується у напрямку осі (або за напрямком одиничного вектора - орта при додатному ); аналогічно – похідна за напрямком осі (або за напрямком орта ). Аналогічно можна визначити поняття похідної за довільним напрямком, який задається одиничним вектором співнаправленим з вектором , де і – напрямні косинуси вектора .

Похідна за напрямком вектора функції у точці обчислюється за формулою:

і визначає швидкість зміни значень функції за цим напрямком.

Приклад . Знайти похідну функції у точці за напрямком вектора .

Розв’язування. Знайдемо частинні похідні функції в точці :

.

.

Знайдемо напрямні косинуси вектора :

; .

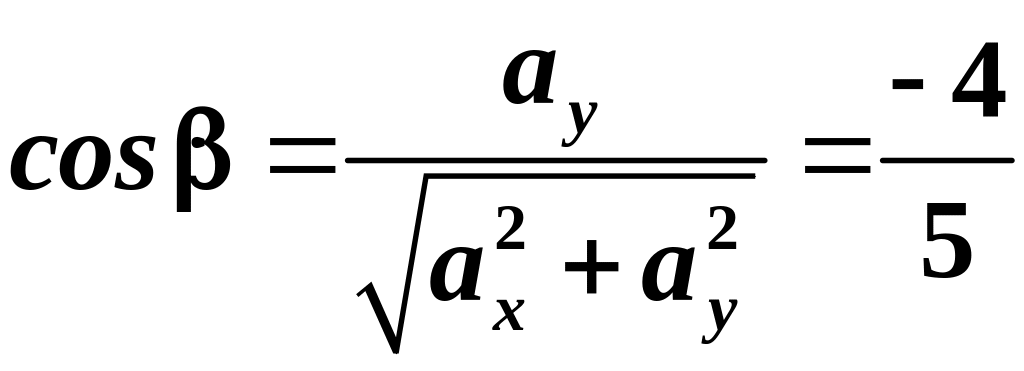За формулою похідної за напрямком отримаємо:

.

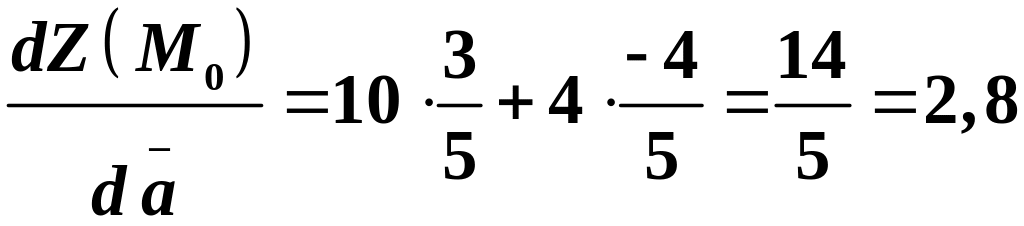Отже, функція у точці за напрямком вектора зростає зі швидкістю .

Зауваження. На відміну від функцій однієї змінної для ФДЗ можна говорити про зростання або спадання лише у певному напрямку.