3. Інтегрування деяких типів диференціальних рівнянь першого порядку.

Найпростішим ДР першого порядку називають рівняння

.

Його загальний розв’язок має вигляд:

.

Нагадаємо, що символом позначається одна із первісних для функції .

Очевидно, що загальний розв’язок найпростішого ДР -го порядку

знаходиться -кратним послідовним інтегруванням.

У попередніх пунктах розв’язувались найпростіші ДР першого та другого порядку (див. приклади 1.3, 1.5, 2.3 а)).

ДР з відокремленими змінними має вигляд:

.

Його загальний інтеграл:

,

де - деяка первісна для функції (вважається, що у цьому інтегралі зроблена заміна змінних ).

ДР з відокремлюваними змінними – це рівняння вигляду:

,

або

,

(3.1)

де функції - неперервні. Нехай . Якщо поділити обидві частини ДР (3.1) на цей добуток, дістанемо ДР з відокремленими змінними:

.

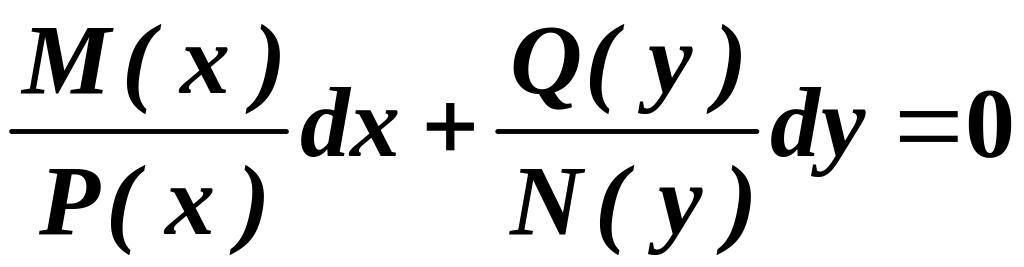Інтегруючи, знаходимо загальний інтеграл:

.

(3.2)

Зауваження 1. Якщо при , , то буде розв’язком ДР (3.1), який неможливо одержати ані при яких значеннях із загального інтегралу (3.2), тобто, особливим розв’язком. Інтегральною кривою в цьому випадку є пряма , паралельна осі .

Зауваження 2. ДР з відокремлюваними змінними (3.1), а також ДР з відокремленими змінними мають симетричний вигляд, тому ніщо не заважає нам вважати невідомою функцією аргумента , тобто, . Це можна використовувати при розв’язуванні таких рівнянь.

Диференціальні рівняння вигляду:

,

зводяться до ДР з відокремлюваними змінними заміною .

Означення. Функція називається однорідною степеня , якщо для всіх виконується рівність .

Наприклад, функції

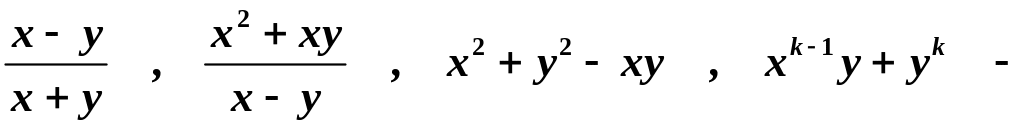
є однорідними відповідно степеня .

Однорідні ДР вигляду:

,

або

,

в яких - однорідна функція степеня нуль, а - однорідні функції одного степеня, заміною зводяться до ДР з відокремлюваними змінними.

Приклад 3.1. Знайти частинний розв’язок ДР , який задовольняє початкову умову .

Розв’язування. Дане рівняння є ДР з відокремленими змінними. Почленно інтегруючи, знаходимо його загальний інтеграл:

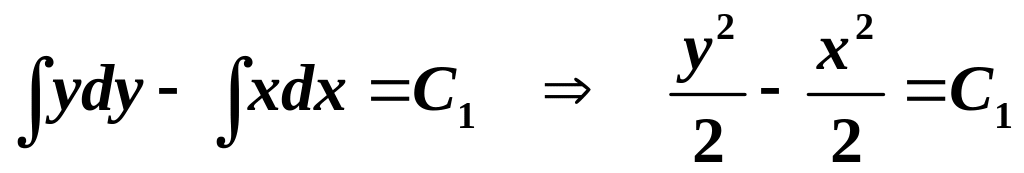, або ,

де - довільна стала. Для знаходження відповідного значення сталої використаємо початкову умову:

.

Отже, частинний інтеграл вихідного ДР, що задовольняє дану початкову умову, має наступний вигляд:

.

Приклад 3.2. Зінтегрувати рівняння

.

Розв’язування. Дане рівняння є ДР з відокремлюваними змінними. Поділивши обидві частини рівняння на добуток , , отримаємо:

.

Змінні відокремлені. Інтегруючи, знаходимо загальний інтеграл вихідного ДР:

, або .

Очевидно, що функції та також будуть розв’язками даного ДР (легко перевіряється підстановкою у вихідне ДР). Ці розв’язки – особливі і були втрачені при діленні обох частин рівняння на .

Приклад 3.3. Розв’язати рівняння

.

Розв’язування. Це ДР з відокремлюваними змінними. Враховуючи, що , дістаємо:

.

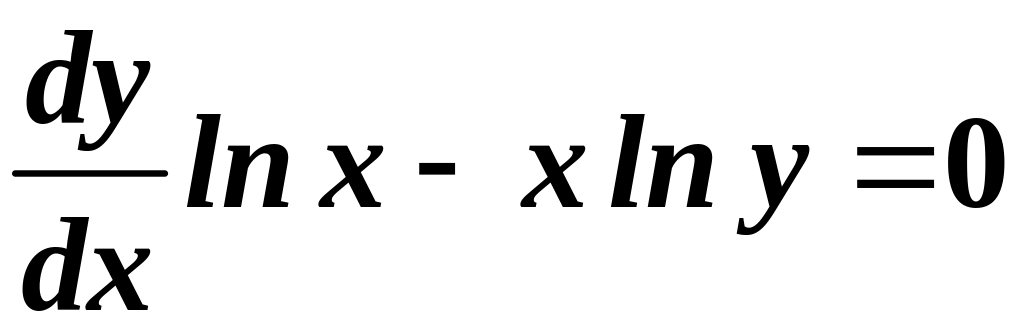Звідси, відокремлюючи змінні, маємо: . Інтегруючи, знаходимо загальний інтеграл:

.

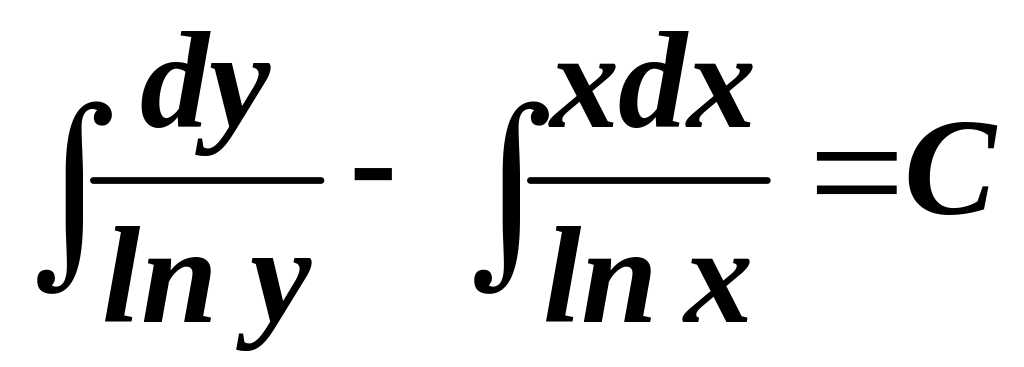Інтеграли у лівій частині останнього співвідношення не виражаються через елементарні функції, але ДР вважається зінтегрованим, оскільки задача зведена до квадратур (інтегралів). Зазначимо також, що функція є розв’язком вихідного ДР (перевіряється безпосередньою підстановкою у ДР: ). Це – особливий розв’язок, який було втрачено при діленні на .

Приклад 3.4. Знайти інтегральну криву ДР

,

що проходить через точку з координатами .

Розв’язування. Маємо ДР з відокремлюваними змінними. Враховуючи, що , і поділивши обидві частини рівняння на добуток , відокремлюємо змінні:

.

Почленно інтегруючи, дістаємо:

, .

(зважаючи на подальші перетворення довільну сталу записано у вигляді ).

Використавши властивості логарифмів, одержуємо:

.

Звідси дістаємо загальний інтеграл ДР (знак модуля розкривається підбором відповідних значень довільної сталої ):

, .

(3.3)

Якщо у цьому співвідношенні допустити, щоб , тобто , то (3.3) задаватиме всі розв’язки вихідного ДР (включаючи і розв’язок , який було втрачено у процесі розв’язання при діленні на ).

Тепер знайдемо частинний інтеграл. Для цього скористуємось початковою умовою :

.

Підставивши знайдене значення у загальний інтеграл (3.3), одержуємо частинний інтеграл

, або ,

(3.4)

який задовольняє початкову умову . Таким чином, співвідношення (3.4) задає на площині інтегральну криву (рівнобічну гіперболу), що проходить через точку з координатами .

Приклад 3.5. Зінтегрувати ДР:

.

Розв’язування. Дане ДР приводиться до вигляду , де . Заміною (із якої дістаємо ) зводимо його до ДР з відокремлюваними змінними:

.

Очевидний розв’язок (пропонуємо впевнитись самостійно): . Знаходимо інші розв’язки, враховуючи, що :

.

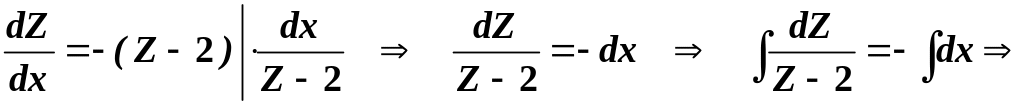
Розв’язок можна дістати з останнього співвідношення при .Тоді:

, або , .

Остаточно, загальний розв’язок вихідного ДР:

.

Приклад 3.6. Розв’язати рівняння

.

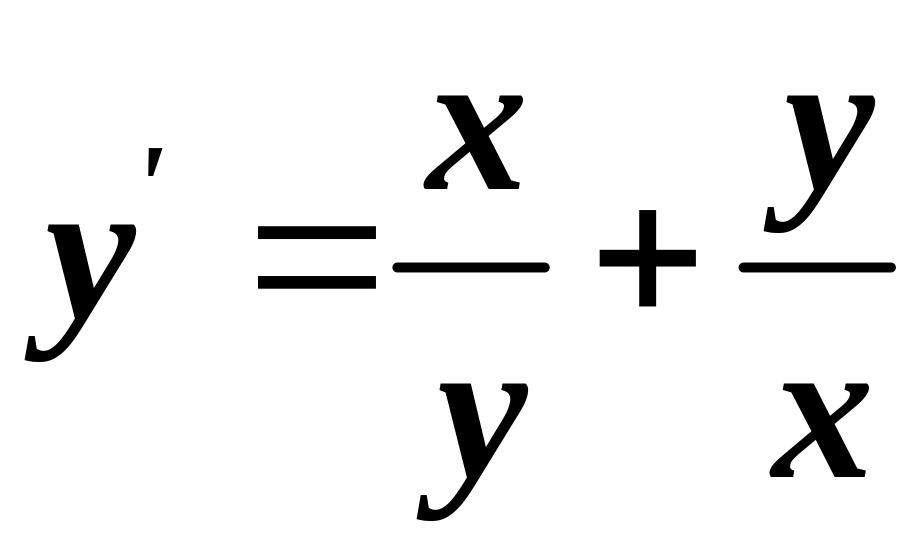Розв’язування. Дане ДР – однорідне, оскільки у правій частині рівняння - однорідна функція. Застосуємо підстановку , де - нова невідома функція:

, , .

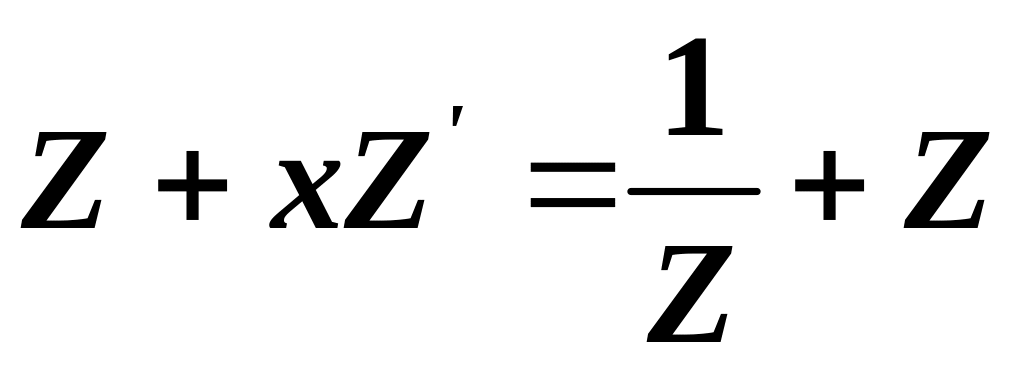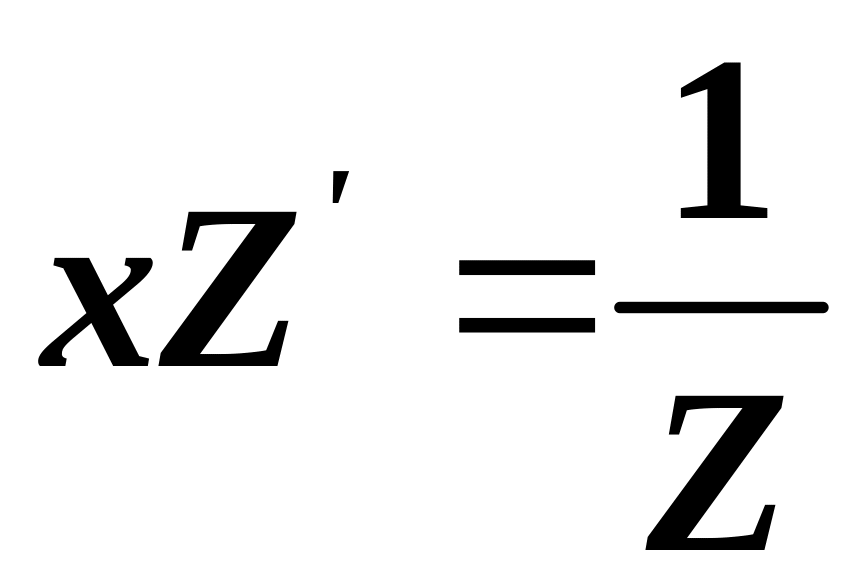Дістали ДР з відокремлюваними змінними. Інтегруючи його, одержуємо:

.

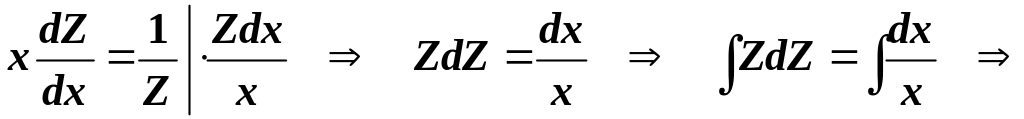
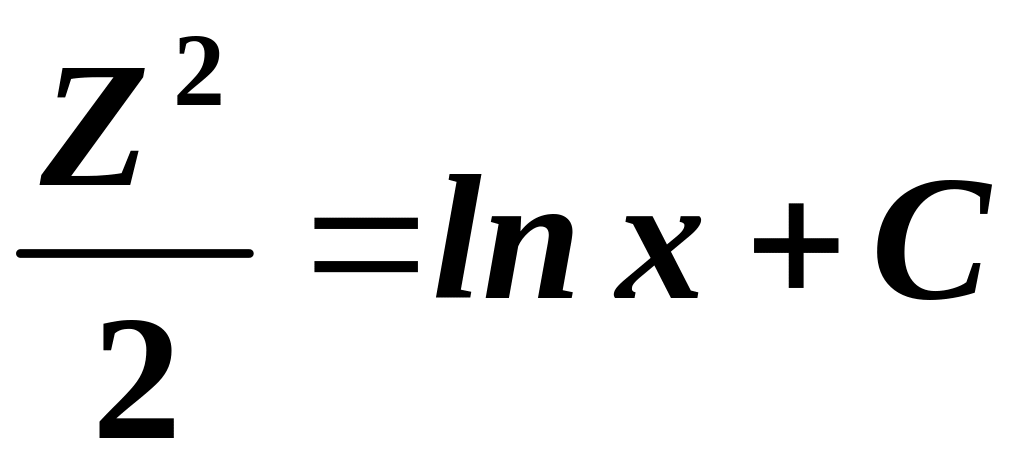Враховуючи, що , повертаємось до змінних та і знаходимо загальний інтеграл вихідного рівняння:

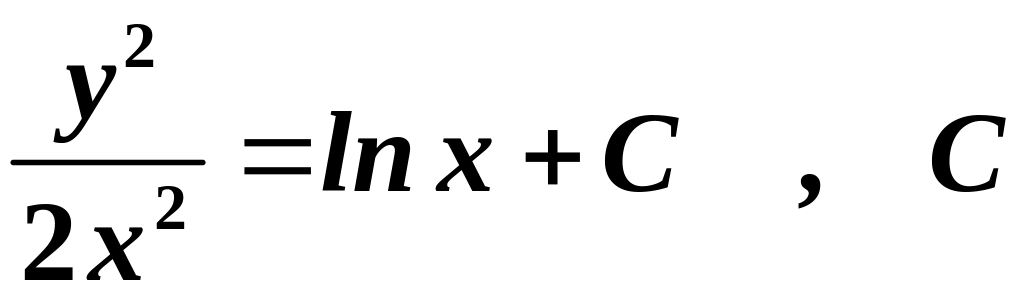- довільна стала.

4. ЛІНІЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ.

Означення. Лінійним ДР першого порядку називається рівняння, лінійне відносно невідомої функції та її похідної , тобто ДР вигляду:

,

де - задані неперервні функції.

Поділивши на , це рівняння завжди можна привести до вигляду:

,

(4.1)

де функції - неперервні. Якщо , то ДР

,

(4.2)

називається лінійним однорідним ДР першого порядку, а при ДР (4.1) називають лінійним неоднорідним ДР першого порядку.

Існує декілька методів розв’язування лінійних ДР: метод Лагранжа (варіації довільної сталої), метод інтегрувального множника та інші. Ми зупинимось на методі Бернуллі, який зводить інтегрування лінійного ДР до розв’язування ДР з відокремлюваними змінними та найпростішого ДР.

Загальний розв’язок лінійного неоднорідного ДР (4.1) будемо розшукувати у вигляді добутку:

,

(4.3)

де нові невідомі функції мають неперервні похідні. Підставляючи добуток (4.3) у ДР (4.1), дістаємо:

,

або

.

(4.4)

Визначимо функцію з умови:

.

Отримали ДР з відокремлюваними змінними (зауважимо, що це ДР є однорідним лінійним ДР вигляду (4.2)). Знаходимо як частинний розв’язок цього ДР:

.

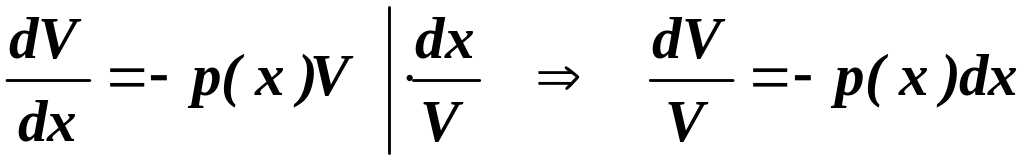Інтегруючи, дістаємо:

.

Покладаючи, наприклад, , одержуємо частинний розв’язок

.

(4.5)

Підставимо знайдену функцію у рівняння (4.4):

.

Домноживши обидві частини останнього рівняння на , для знаходження функції дістаємо найпростіше ДР:

.

Його загальний розв’язок:

.

(4.6)

Знайдені функції (4.5) та (4.6) підставляємо у (4.3) і дістаємо загальний розв’язок лінійного ДР (4.1):

,

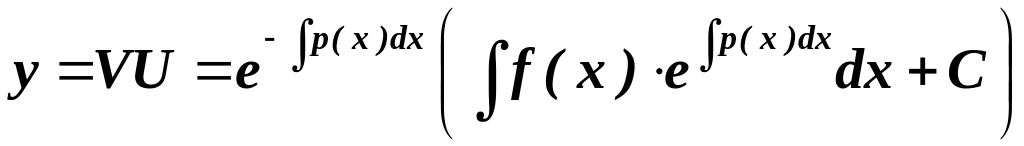або

.

Зауваження. Загальний розв’язок лінійного неоднорідного ДР (4.1) має вигляд:

,

де - загальний розв’язок відповідного лінійного однорідного ДР (4.2), а 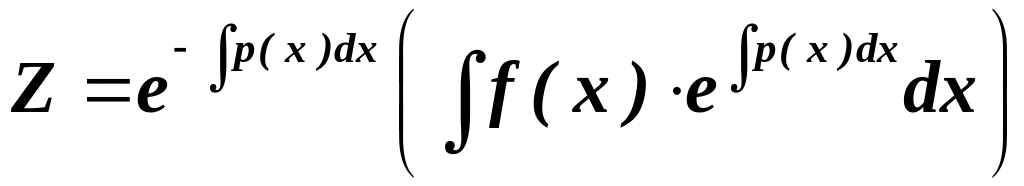- частинний розв’язок (пропонуємо впевнитись у цьому самостійно) лінійного неоднорідного ДР (4.1). Виявляється (і це неважко довести), що таку структуру мають загальні розв’язки лінійних ДР -го порядку. Нижче це буде показано для лінійних ДР другого порядку зі сталими коефіцієнтами.

Крім того, рекомендуємо при інтегруванні лінійних ДР першого порядку не користуватись готовою формулою загального розв’язку, а кожного разу робити підстановку (4.3).

Приклад 4.1. Розв’язати рівняння

.

Розв’язування. Дане лінійне ДР першого порядку діленням на приводиться до вигляду (4.1):

.

Застосуємо підстановку :

,

(4.7)

.

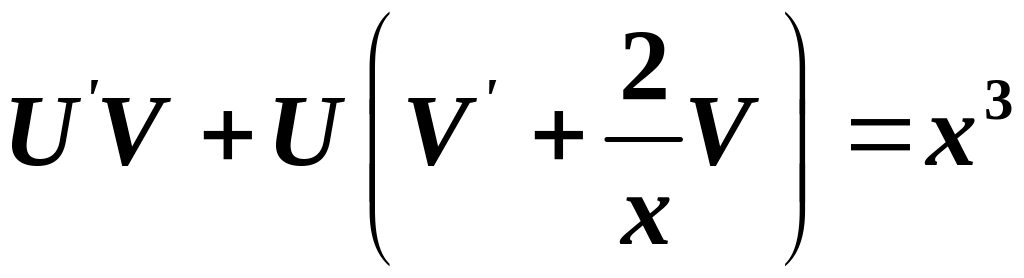Знаходимо функцію як частинний розв’язок ДР з відокремлюваними змінними:

.

.

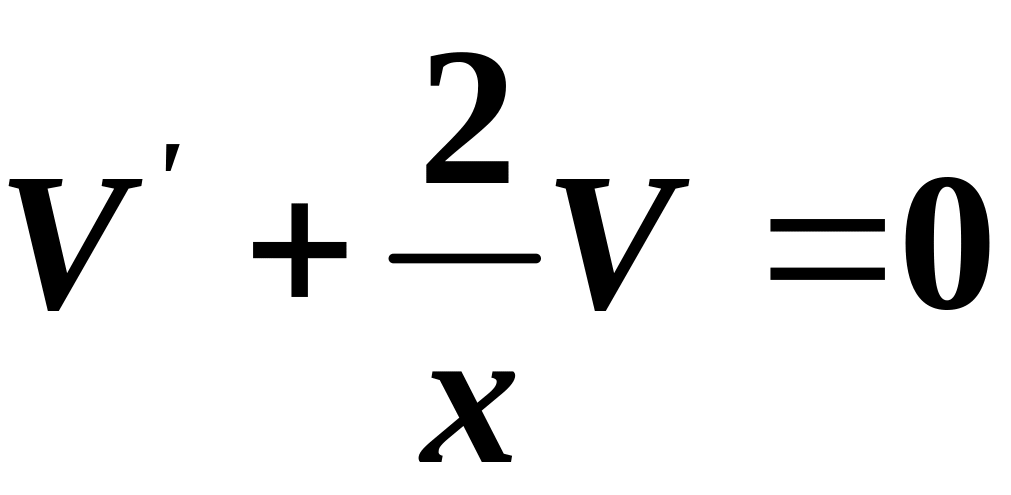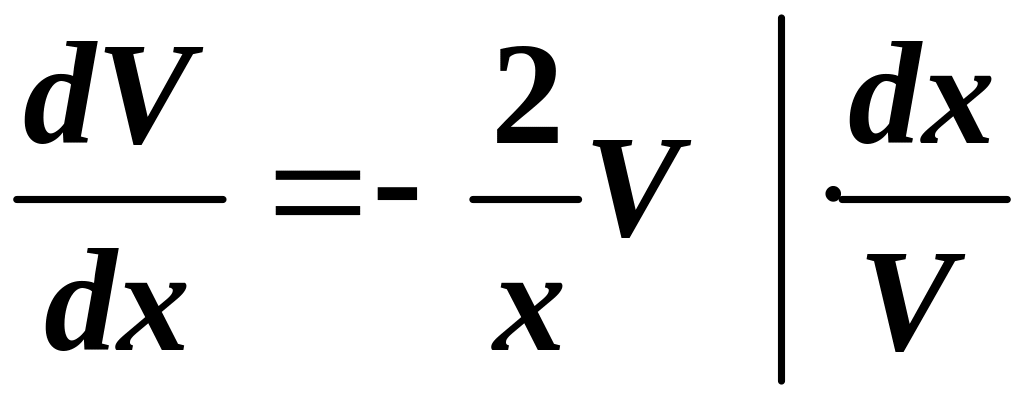
Інтегруванням отримуємо:

.

Покладаючи , одержуємо частинний інтеграл:

.

Звідси потенціюванням дістаємо:

.

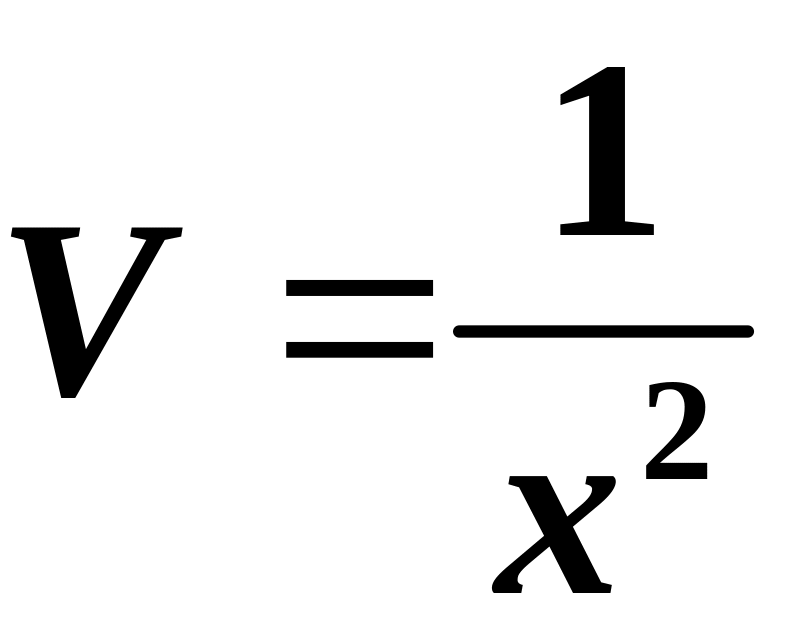Підставимо знайдену функцію у рівняння (4.7):

.

Знаходимо функцію як загальний розв’язок останнього найпростішого ДР:

.

Отже, загальний розв’язок вихідного лінійного ДР має вигляд:

,

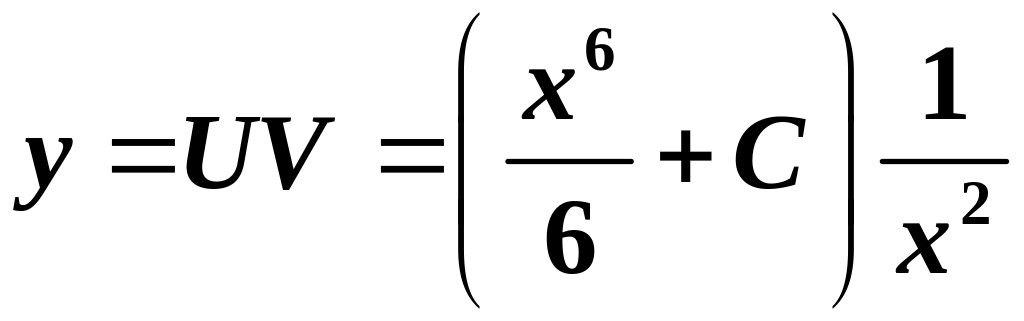або

.

Зауважимо, що деякі ДР стають лінійними, якщо вважати аргументом, а - невідомою функцією.

Приклад 4.2. Розв’язати задачу Коші для ДР

з початковою умовою .

Розв’язування. Дане ДР, очевидно, нелінійне відносно . Перепишемо його у вигляді:

.

Домноживши обидві частини останнього рівняння на , дістанемо:

.

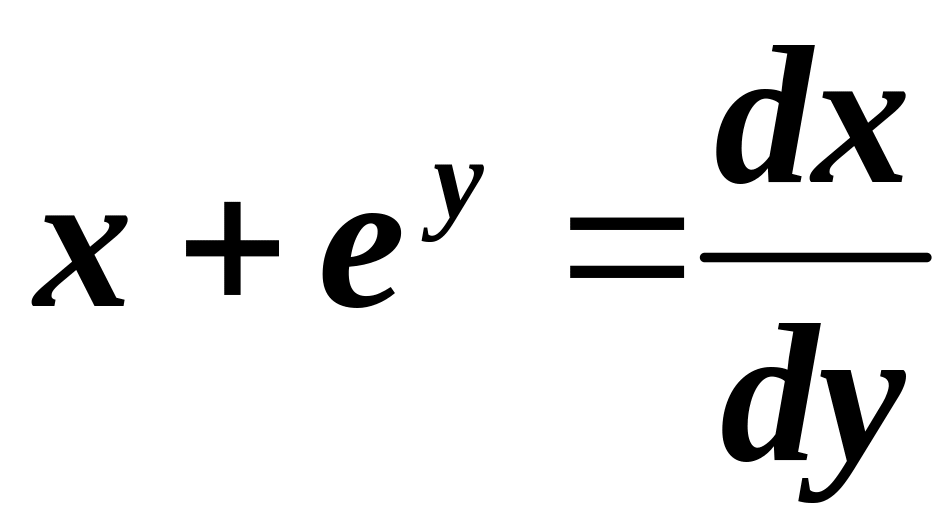Відносно функції маємо лінійне ДР вигляду (4.1):

,

(4.8)

де 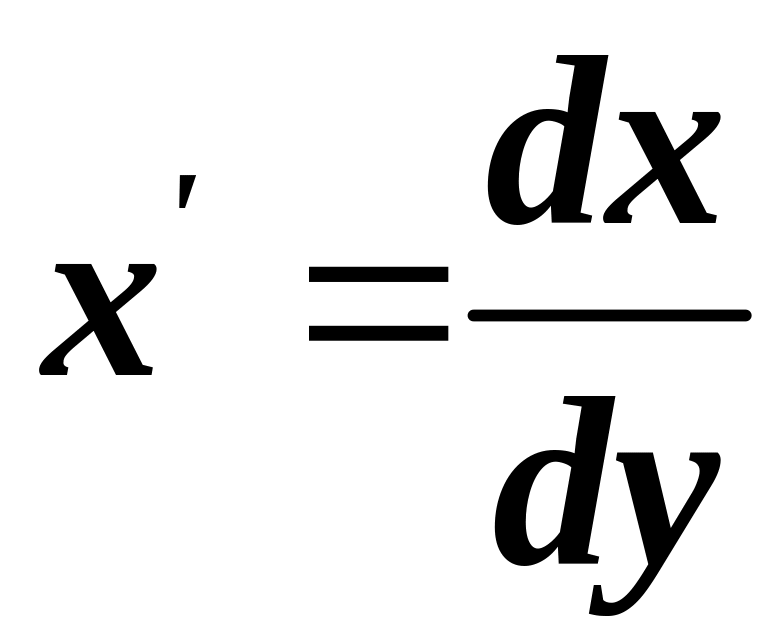, а - неперервні функції аргументу .

Застосуємо підстановку :

.

(4.9)

Знаходимо функцію як частинний розв’язок ДР з відокремлюваними змінними:

.

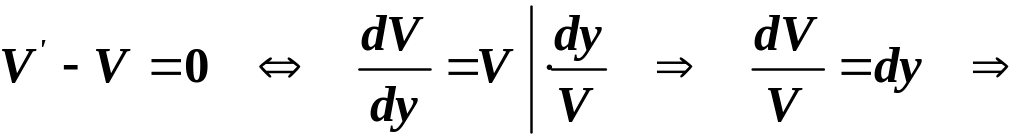
Покладаючи , дістаємо , звідси: . Повертаючись до (4.9), для знаходження функції отримуємо найпростіше ДР:

.

Отже, .

Перемноживши функції та , одержуємо загальний розв’язок лінійного ДР (4.8):

.

Підставляючи у цей загальний розв’язок початкову умову , знаходимо відповідне значення сталої : і записуємо шуканий частинний розв’язок:

.

Зауважимо, що отриманий частинний розв’язок лінійного ДР (4.8) є частинним інтегралом вихідного ДР, який задовольняє початкову умову .

5. ЛІНІЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ДРУГОГО ПОРЯДКУ

ЗІ СТАЛИМИ КОЕФІЦІЄНТАМИ.

Означення. Лінійним ДР другого порядку зі сталими коефіцієнтами називається рівняння, лінійне відносно невідомої функції та її похідних і :

,

де - сталі коефіцієнти, а - задана неперервна функція.

Очевидно, що поділивши обидві частини рівняння на , його завжди можна привести до вигляду:

,

(5.1)

де - сталі коефіцієнти, а функція - неперервна.

Рівняння вигляду (5.1) у випадку, коли , будемо називати лінійним неоднорідним ДР другого порядку (скорочено - ЛНДР).

У випадку, коли , рівняння

,

(5.2)

називається лінійним однорідним ДР другого порядку (скорочено - ЛОДР).

Властивості розв’язків ЛОДР.

Теорема 1. Якщо - розв’язок (частинний) ЛОДР (5.2), то функція , де - будь-яке дійсне число, також є розв’язком ЛОДР (5.2).

Доведення. Так як розв’язок ЛОДР (5.2), то справедлива тотожність:

.

Підставляючи функцію у ЛОДР (5.2) і враховуючи, що сталий множник виноситься за знак похідної, дістаємо:

.

Отже, функція є розв’язком ЛОДР (5.2), оскільки перетворює це рівняння в тотожність.

Теорема 2. Якщо функції - розв’язки ЛОДР (5.2), то їх сума також є розв’язком цього рівняння.

Доведення. Так як - розв’язки ЛОДР (5.2), то

, .

Підставляючи функцію у рівняння (5.2) і враховуючи,що похідна суми дорівнює сумі похідних, дістаємо:

.

Оскільки функція перетворює рівняння в тотожність, ця сума є розв’язком ЛОДР (5.2), що і потрібно було довести.

Із теорем 1,2 випливає наступна

Теорема 3. Якщо - розв’язки ЛОДР (5.2), то їх лінійна комбінація , де - будь-які дійсні числа, також є розв’язком ЛОДР (5.2).

Пропонуємо цю теорему довести самостійно.

Зауваження. Теореми 1-3 справедливі для ЛОДР будь-якого порядку, причому коефіцієнтами рівняння можуть бути довільні неперервні функції.

Означення. Функції називаються лінійно залежними, якщо їх відношення дорівнює сталому числу , тобто (або ). У супротивному випадку функції називають лінійно незалежними.

Наприклад: функції - лінійно залежні, оскільки їх відношення ; а функції - лінійно незалежні, оскільки .

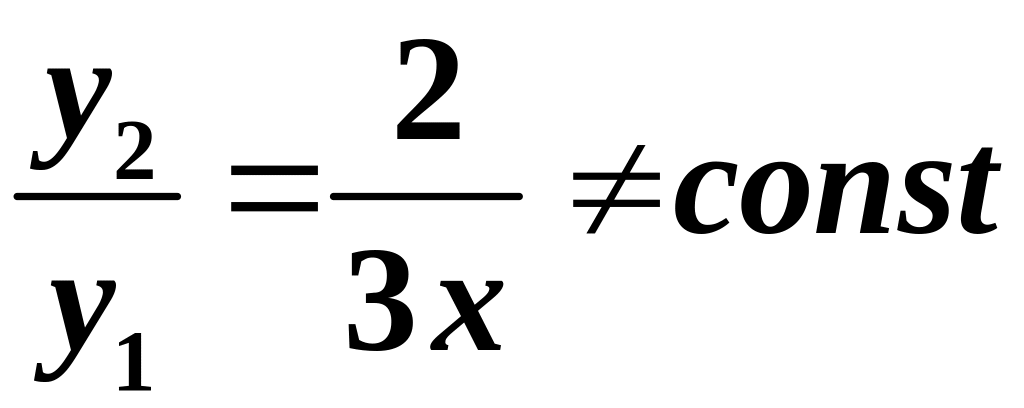Зауваження. При розв’язуванні задачі Коші для ДР другого порядку, його частинні розв’язки знаходять із загального розв’язку, користуючись початковими умовами .

Справедлива наступна

Теорема 4 (структура загального розв’язку ЛОДР другого порядку). Якщо функції - лінійно незалежні розв’язки ЛОДР (5.2), то функція

(5.3)

є загальним розв’язком цього рівняння (тут і надалі: - довільні сталі).

Доведення. З теореми 3 випливає, що функція є розв’язком ЛОДР (5.2) при всіх значеннях . Покажемо, що будь-який частинний розв’язок ЛОДР (5.2), який задовольняє дані початкові умови, можна отримати із загального розв’язку (5.3). Продиференціювавши (5.3): і скориставшись початковими умовами (див. попереднє зауваження), для знаходження відповідних значень сталих дістаємо систему лінійних алгебраїчних рівнянь:

.

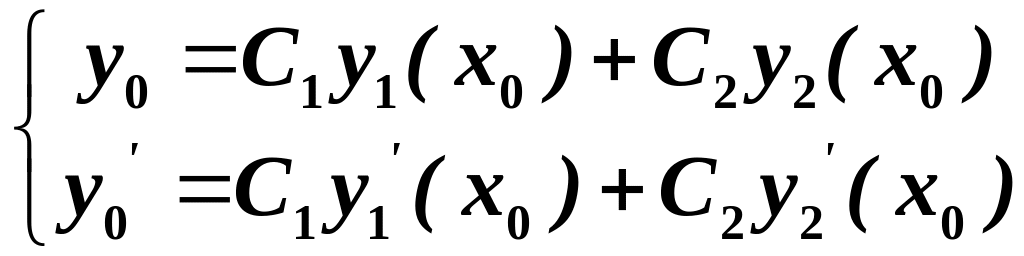Визначник цієї системи:

як визначник Вронського для лінійно незалежних функцій . Тому система має єдиний розв’язок.

Таким чином, функція (5.3) задовольняє всім умовам, що накладаються на загальний розв’язок (при будь-яких значеннях сталих є розв’язком ЛОДР і будь-який частинний розв’язок, що задовольняє дані початкові умови, можна дістати із (5.3) при певних значеннях сталих). Теорему доведено.

З теореми 4 робимо висновок, що для знаходження загального розв’язку ЛОДР (5.2) потрібно знайти два його лінійно незалежні розв’язки і записати їх лінійну комбінацію.

Розв’язки ЛОДР (5.2) будемо розшукувати у вигляді показникової функції , де - деяке число (ідея Ейлера). Підставляючи цю функцію у рівняння (5.2), одержуємо:

,

,

.

Оскільки для будь-яких , то остання тотожність справедлива тоді і тільки тоді, коли число є коренем квадратного рівняння:

,

яке називають характеристичним рівнянням ЛОДР (5.2).

Позначимо через дискримінант характеристичного рівняння і розглянемо три можливих випадки: , та .

Теорема 5 (випадок ). Якщо характеристичне рівняння має два дійсних відмінних кореня , то загальний розв’язок ЛОДР (5.2) має вигляд:

.

(5.4)

Доведення. Функції та є розв’язками ЛОДР (5.2), оскільки - корені характеристичного рівняння. Ці функції – лінійно незалежні, так як їх відношення , враховуючи, що . За теоремою 4, загальним розв’язком ЛОДР (5.2) буде функція (5.4).

Теорема 6 (випадок ). Якщо характеристичне рівняння має співпадаючі корені , то загальний розв’язок ЛОДР (5.2) має наступний вигляд:

.

(5.5)

Доведення. Очевидно, що функція є розв’язком ЛОДР (5.2), оскільки - корінь характеристичного рівняння. Впевнимось, що функція також є розв’язком ЛОДР (5.2). Підставляючи у рівняння (5.2), дістаємо:

,

оскільки вираз в квадратних дужках дорівнює нулю (зважаючи на те, що 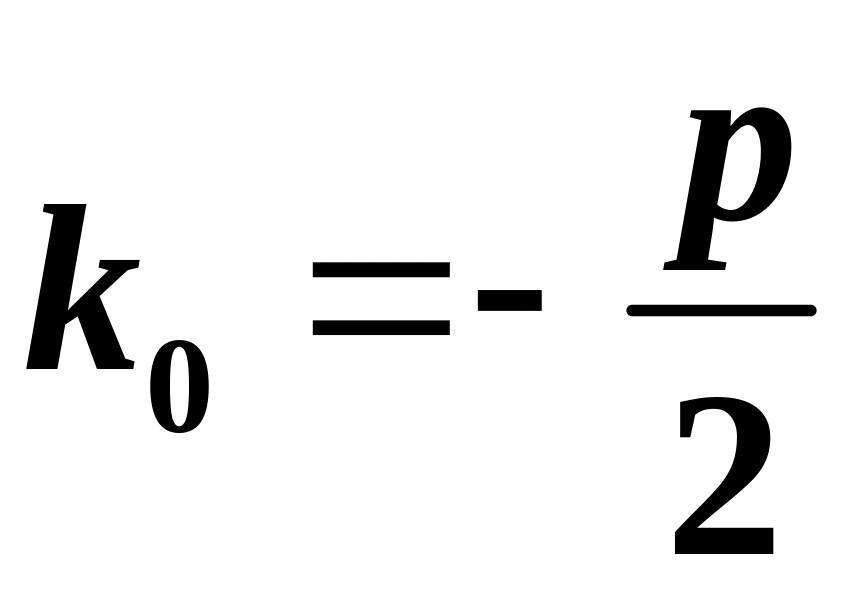- кратний корінь характеристичного рівняння).

Відношення 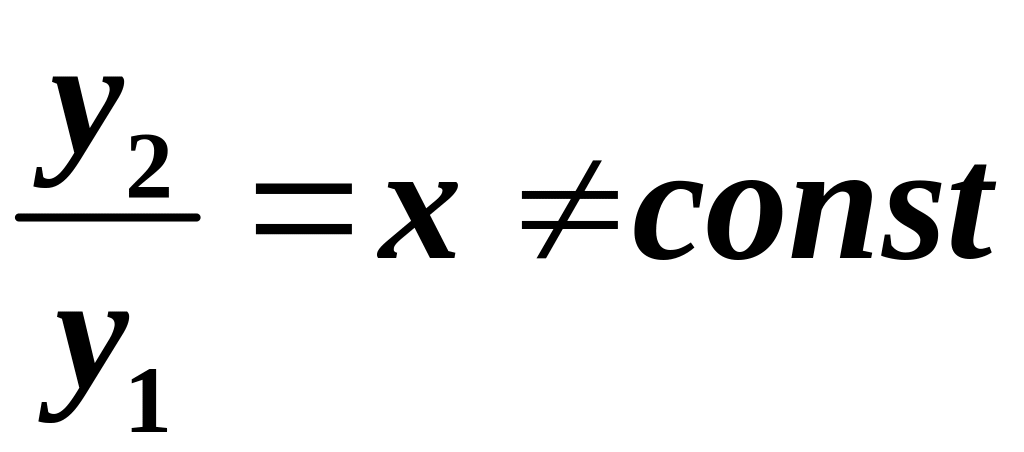, отже функції та лінійно незалежні. За теоремою 4, лінійна комбінація цих функцій (тобто, функція (5.5)) є загальним розв’язком ЛОДР (5.2).

Теорема 7 (випадок ). Якщо характеристичне рівняння не має дійсних коренів, то загальний розв’язок ЛОДР (5.2) має наступний вигляд:

,

(5.6)

де .

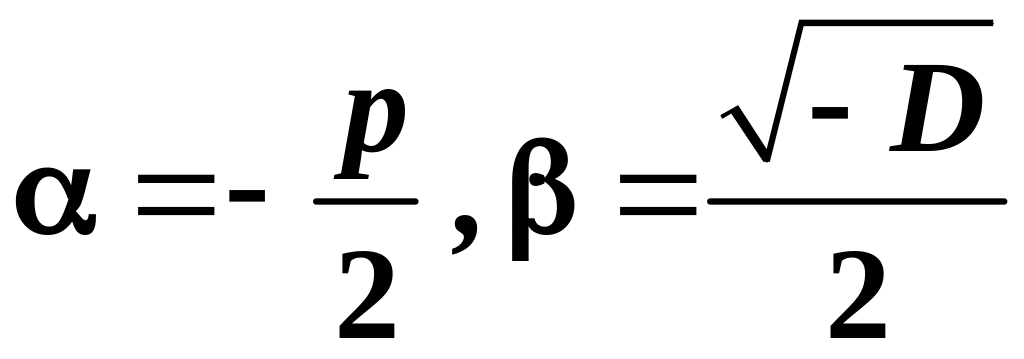Доведення. Покажемо, що функція є розв’язком ЛОДР (5.2). Знайдемо похідні :

,

.

Підставляючи у ЛОДР (5.2), одержуємо:

.

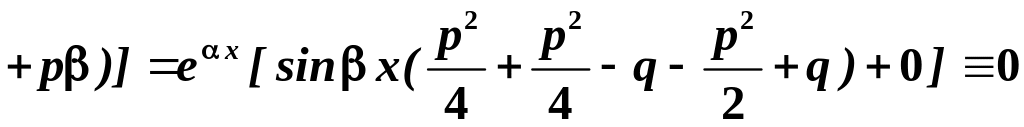Отже, функція є розв’язком ЛОДР (5.2).

Аналогічно доводиться, що функція також є розв’язком ЛОДР (5.2). Оскільки розв’язки та лінійно незалежні (їх відношення 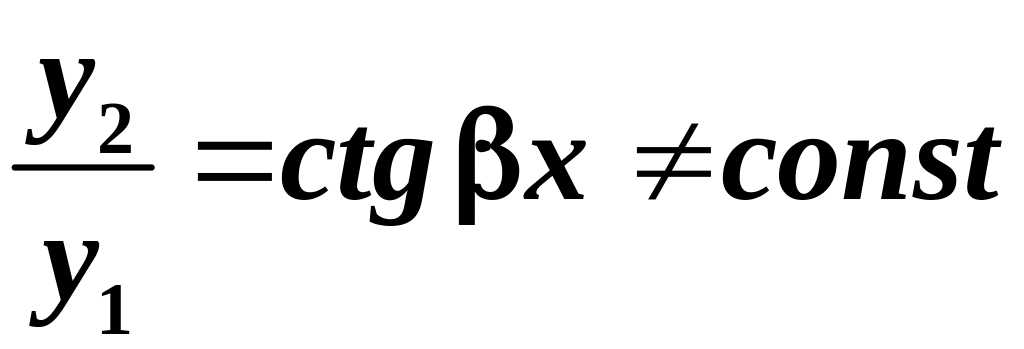), то, за теоремою 4, функція (5.6)

є загальним розв’язком ЛОДР (5.2).

Приклад 5.1. Знайти частинний розв’язок рівняння

,

який задовольняє початкові умови .

Розв’язування. Дане рівняння – це ЛОДР другого порядку вигляду (5.2). Для знаходження його загального розв’язку складемо характеристичне рівняння:

.

Його дискримінант , а корені: . За теоремою 5 загальний розв’язок матиме вигляд:

.

Звідси

.

Використовуючи початкові умови та враховуючи вигляд і , для визначення відповідних значень сталих дістаємо систему рівнянь:

.

Розв’язуючи цю систему, знаходимо .

Отже, шуканий частинний розв’язок вихідного ЛОДР, який задовольняє дані початкові умови, має вигляд:

.

Приклад 5.2. Розв’язати рівняння

.

Розв’язування. Маємо ЛОДР другого порядку зі сталими коефіцієнтами. Для знаходження загального розв’язку складемо характеристичне рівняння:

.

Його корені: , оскільки . За теоремою 6 загальний розв’язок вихідного рівняння має вигляд:

.

Приклад 5.3. Знайти загальний розв’язок ДР

.

Розв’язування. Дане рівняння – це ЛОДР другого порядку зі сталими коефіцієнтами. Приведемо його спочатку до вигляду (5.2), поділивши обидві частини на 2. Одержуємо:

.

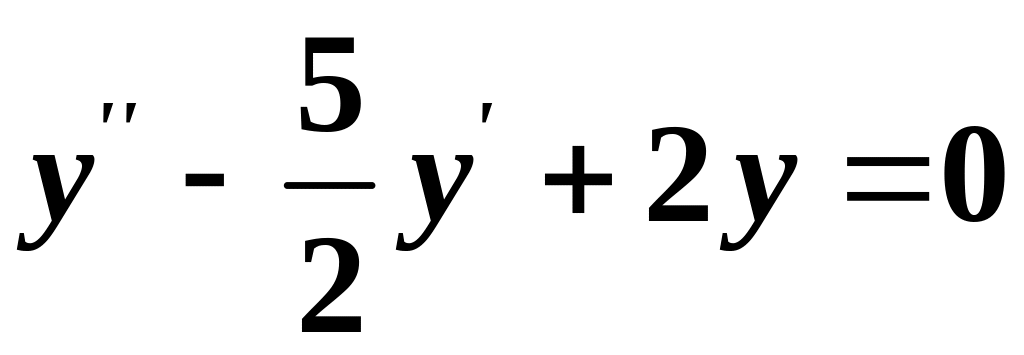Дискримінант характеристичного рівняння :

.

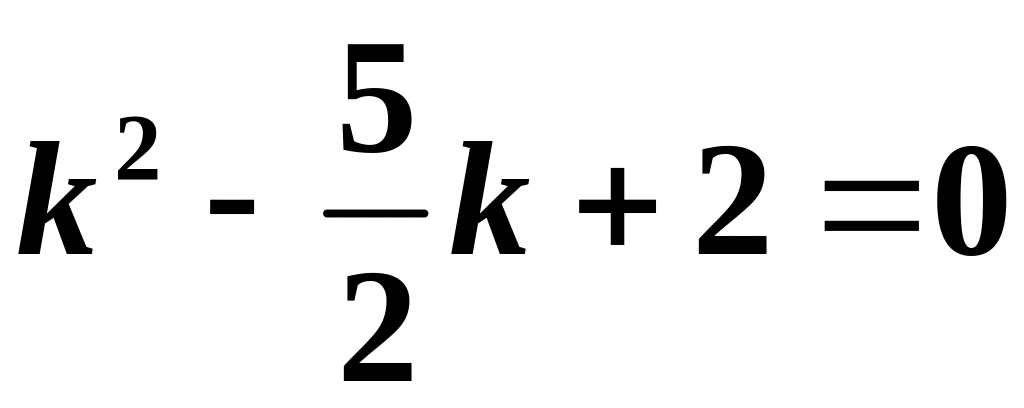Тому, за теоремою 7, знаходимо числа:

.

Отже, загальний розв’язок вихідного ДР (згідно теоремі 7) має вигляд:

.

Розглянемо тепер ЛНДР, тобто лінійні неоднорідні ДР другого порядку зі сталими коефіцієнтами вигляду (5.1):

.

Теорема 8 (структура загального розв’язку ЛНДР другого порядку). Загальний розв’язок ЛНДР (5.1) має наступний вигляд:

,

(5.7)

де - загальний розв’язок відповідного ЛОДР, а - довільний частинний розв’язок ЛНДР (5.1).

Доведення. Оскільки - загальний розв’язок відповідного ЛОДР, а - деякий частинний розв’язок ЛНДР, то справедливі тотожності:

, .

Підставимо функцію (5.7) у ЛНДР. Враховуючи, що похідна суми дорівнює сумі похідних, після нескладних перетворень, одержуємо:

.

Зважаючи на те, що містить дві незалежні довільні сталі , робимо висновок, що функція є загальним розв’язком ЛНДР (5.1).

Зауважимо, що доведення єдиності розв’язку задачі Коші для ЛНДР (5.1) проводиться аналогічно теоремі 4.

Знаходження загального розв’язку ЛОДР було розглянуто вище, тому виникає питання знаходження частинних розв’язків ЛНДР.

Розглянемо найпростіший випадок знаходження частинних розв’язків ЛНДР (5.1), коли права частина цього рівняння має спеціальний вигляд:

,

(5.8)

де - дійсне число, а - многочлен степеня .

А. Якщо не співпадає з жодним із коренів характеристичного рівняння відповідного ЛОДР, то частинний розв’язок ЛНДР (5.1) шукають у вигляді:

,

(5.9)

де - многочлен степеня (як і ) загального вигляду із невизначеними коефіцієнтами.

Б. Якщо (тобто співпадає з одним із коренів характеристичного рівняння), то частинний розв’язок ЛНДР шукають у вигляді:

,

(5.10)

В. Якщо (тобто співпадає із обома коренями характеристичного рівняння), то частинний розв’язок ЛНДР шукають у вигляді:

,

(5.11)

Зауваження. Всі три випадки А,Б і В можна об’єднати в одну формулу:

,

де число приймає значення у випадках А,Б,В відповідно.

Приклад 5.4. Розв’язати задачу Коші для диференціального рівняння

,

з початковими умовами .

Розв’язування. Спочатку знайдемо загальний розв’язок відповідного ЛОДР:

.

Корені характеристичного рівняння : , тому, за теоремою 5, загальний розв’язок відповідного ЛОДР:

.

У правій частині вихідного рівняння функція

вигляду (5.8), причому , а - многочлен першого степеня. Оскільки не співпадає з жодним із коренів характеристичного рівняння, то частинний розв’язок ЛНДР шукаємо у вигляді (5.9):

.

Знаходимо похідні:

, .

Підставляючи у вихідне ЛНДР, дістаємо тотожність:

,

або, скоротивши обидві частини на ,

.

Зрівнюючи коефіцієнти при однакових степенях змінної , знаходимо: .

Таким чином, частинний розв’язок вихідного НЛДР має вигляд:

,

а його загальний розв’язок :

.

Знайдемо похідну:

.

Враховуючи вигляд та , використаємо задані початкові умови для знаходження відповідних значень сталих і . Дістанемо систему рівнянь:

.

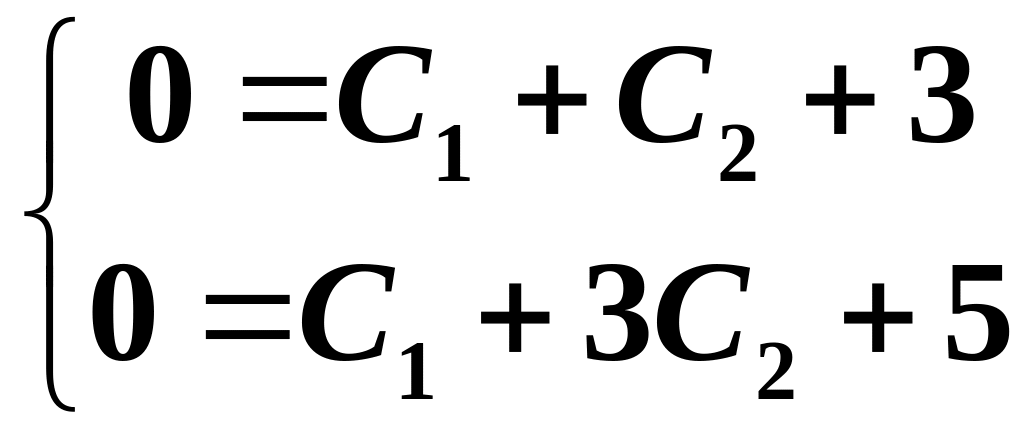Розв’язуючи її, отримуємо: .

Остаточно, шуканий частинний розв’язок вихідного ЛНДР, що задовольняє заданим початковим умовам, має вигляд:

.

Приклад 5.5. Розв’язати рівняння:

.

Розв’язування. Складаємо характеристичне рівняння відповідного ЛОДР: , корені якого: . Тому, загальний розв’язок ЛОДР за теоремою 5 матиме вигляд:

.

Права частина вихідного ЛНДР має вигляд (5.8):

,

де (співпадає з одним із коренів характеристичного рівняння), а - многочлен першого степеня. Тому частинний розв’язок ЛНДР шукаємо у вигляді (5.10):

.

Знаходимо похідні:

.

Підставляючи їх у вихідне ЛНДР, дістанемо тотожність:

,

з якої визначаємо коефіцієнти та :

.

Отже, частинний розв’язок вихідного ЛНДР:

,

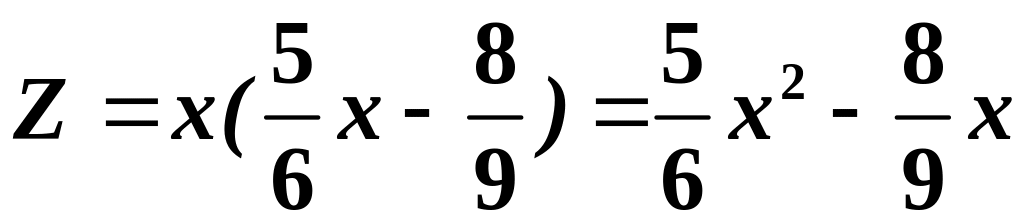а його загальний розв’язок:

.

Зауваження. Очевидно, всі положення даного пункту справедливі також і для лінійних ДР першого порядку зі сталими коефіцієнтами вигляду

,

де - дійсне число, а - задана неперервна функція. Продемонструємо це на прикладі 3.5 (див. пункт 3):

,

яке можна розглядати як лінійне ДР першого порядку зі сталими коефіцієнтами ( ). Характеристичне рівняння відповідного однорідного ДР : має корінь , тому загальний розв’язок однорідного рівняння:

.

Права частина має спеціальний вигляд (добуток многочлена на експоненту). Маємо випадок А, тому частинний розв’язок неоднорідного ДР шукаємо у вигляді . Підставивши у вихідне рівняння і зрівнявши коефіцієнти при відповідних степенях , дістаємо: . За теоремою 8, загальний розв’язок вихідного ДР має вигляд (порівняй із відповіддю цього прикладу 3.5 у пункті 3):

.

Розділ 1. Функції декількох змінних (ФДЗ)