Деякі методи інтегрування Безпосереднє інтегрування.

Безпосереднє інтегрування – це такий спосіб інтегрування, при якому, користуючись алгебраїчними та іншими перетвореннями, а також властивостями невизначених інтегралів, заданий інтеграл зводиться до табличного.

Приклад . Знайти інтеграли:

1. .

2. .

3. 

.

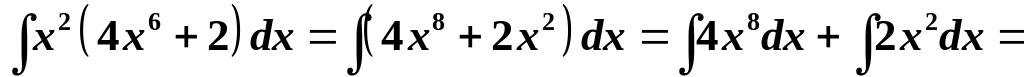
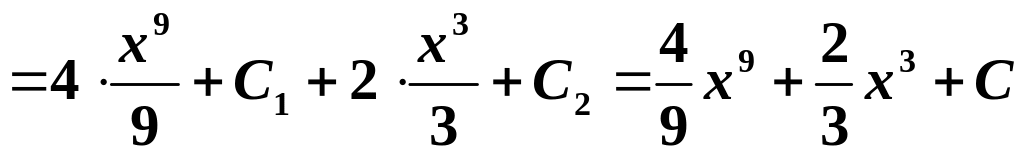Зауваження. Декілька сталих інтегрування можна об’єднати в одну, оскільки сума декількох довільних сталих є також довільна стала.

г)

.

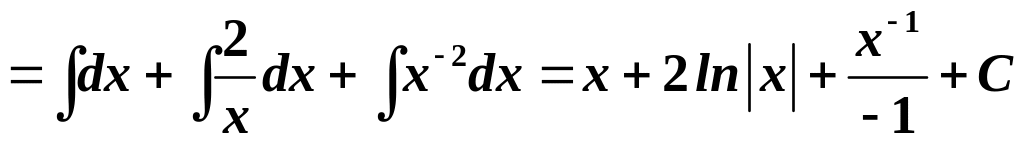д)

.

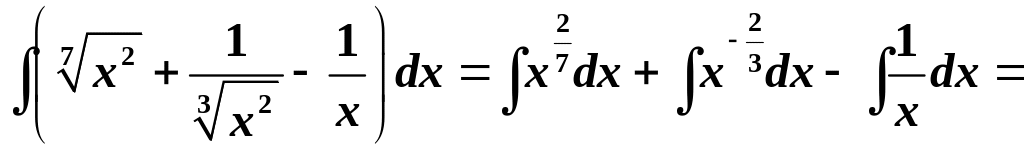
Приклад . Знайти невизначені інтеграли:

1. .

2. .

3. .

4. .

5. 

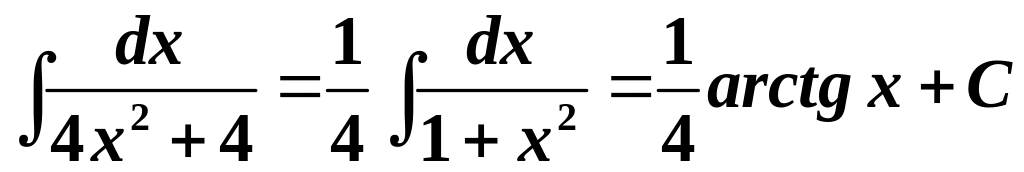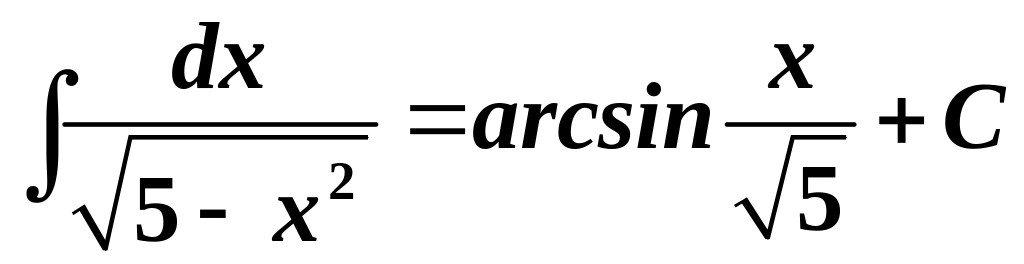Заміна змінної у невизначеному інтегралі.

Теорема. Нехай - складна функція, аргументом якої є - неперервно диференційовна функція аргумента . Тоді справедлива формула заміни змінної у невизначеному інтегралі:

.

Доведення. Нехай - первісна для функції , тобто: . Доведемо, що - також є первісною для підінтегральної функції у правій частині формули. Для цього знайдемо її похідну по аргументу :

.

Теорему доведено.

Зауваження. На практиці, у багатьох випадках роблять заміну змінних «навпаки», позначаючи , виражаючи потім через . Окрім того, доцільність заміни виправдана, якщо відносно нової змінної отримується інтеграл простіший у порівнянні з даним інтегралом.

Приклад . Знайти невизначені інтеграли:

1. .

2. .

3. .

4. .

5.

.

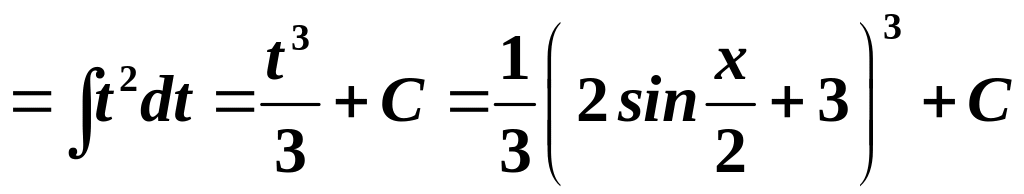6.

.

Інтегрування частинами.

Теорема. Якщо та - неперервно диференційовні функції, тоді справедлива формула інтегрування частинами:

.

Доведення. За правилом знаходження диференціала добутку функцій маємо:

.

Звідси . Проінтегруємо обидві частини і застосуємо властивість інтеграла від алгебраїчної суми функцій:

.

Враховуючи властивість інтеграла від диференціала функції, дістаємо:

.

Формулу доведено.

Метод інтегрування, що ґрунтується на застосуванні цієї формули, називається методом інтегрування частинами.

При цьому підінтегральний вираз розбивається на добуток двох частин: і , вибір яких обумовлений, як правило, наступними міркуваннями: похідна повинна бути простішою за , а – табличний або ж його знаходження не пов’язане з великими труднощами. Відзначимо два основні типи інтегралів, які знаходяться за допомогою метода інтегрування частинами (причому, є певні рекомендації стосовно вибору і ). Це інтеграли виду:

,

де - многочлен степеня , а - функція з одного із двох типів:

І. 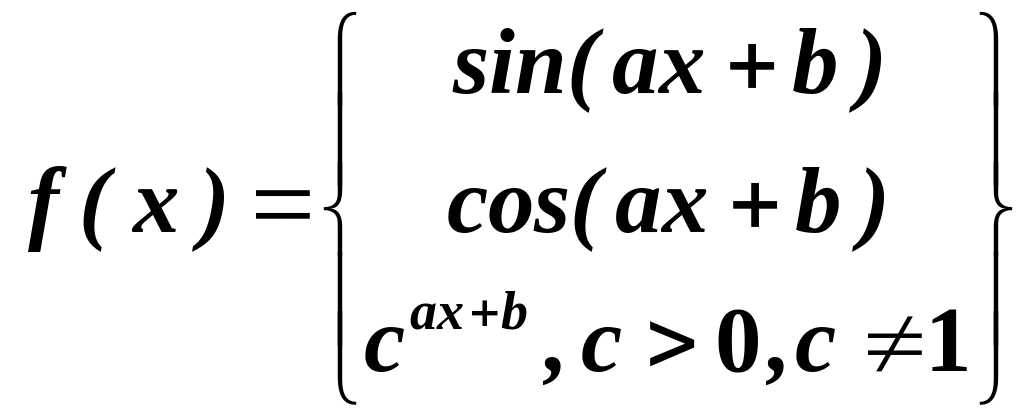, - лінійні функції.

У цьому випадку рекомендується при застосуванні формули інтегрування частинами вибирати в якості многочлен , оскільки при диференціюванні його степінь понижується, а в якості , оскільки інтеграли від - це функції того ж типу.

ІІ. .

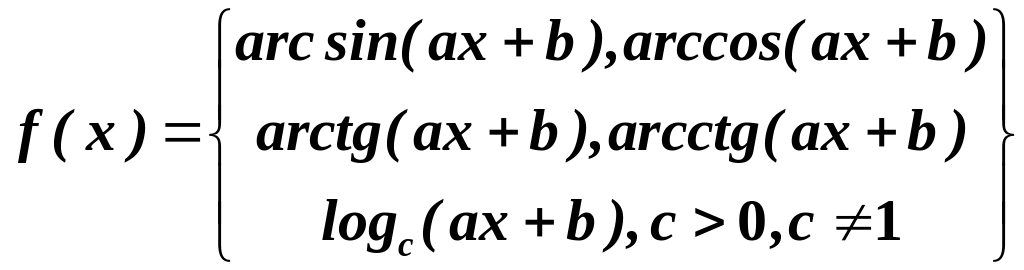У цьому випадку рекомендується при застосуванні формули інтегрування частинами вибирати в якості обернену тригонометричну або логарифмічну функцію, оскільки при диференціюванні отримуються раціональні функції, а в якості , оскільки інтеграли від теж є многочленами.

Приклад . Знайти інтеграли:

а) . Цей інтеграл належить до І типу. Тому:

.

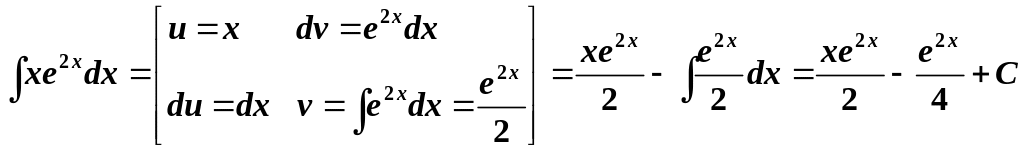б) . Цей інтеграл належить до І типу. Тому:

.

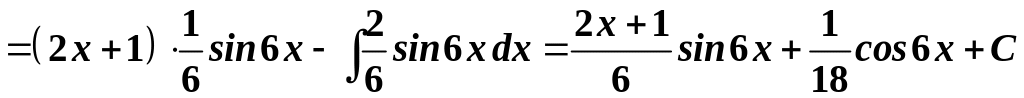в) . Цей інтеграл належить до І типу. Тому:

.

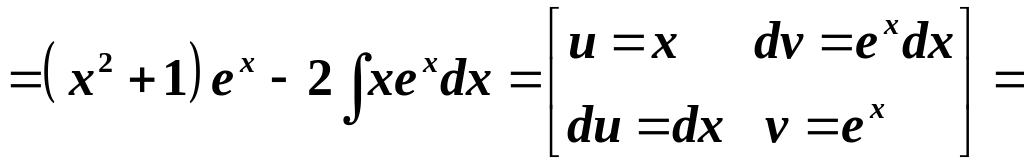
г) . Цей інтеграл належить до ІІ типу. Тому:

.

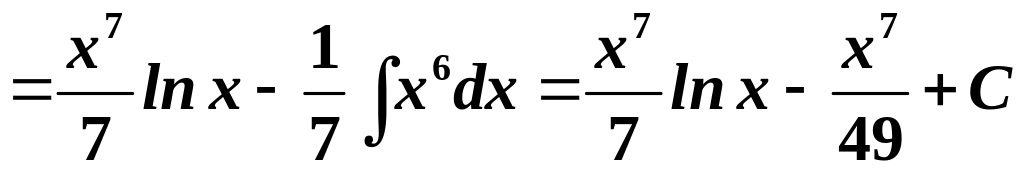д) . Цей інтеграл належить до ІІ типу. Тому:

.

За допомогою методу інтегрування частинами можна знаходити й інші інтеграли, наприклад,

д)

.