Обчислення площ плоских фігур за допомогою визначеного інтеграла.

Задача 1. Знайти площу фігури, обмеженої лініями . Якщо функція та неперервна на відрізку , то із геометричного змісту визначеного інтегралу випливає, що площа обчислюється за формулою: 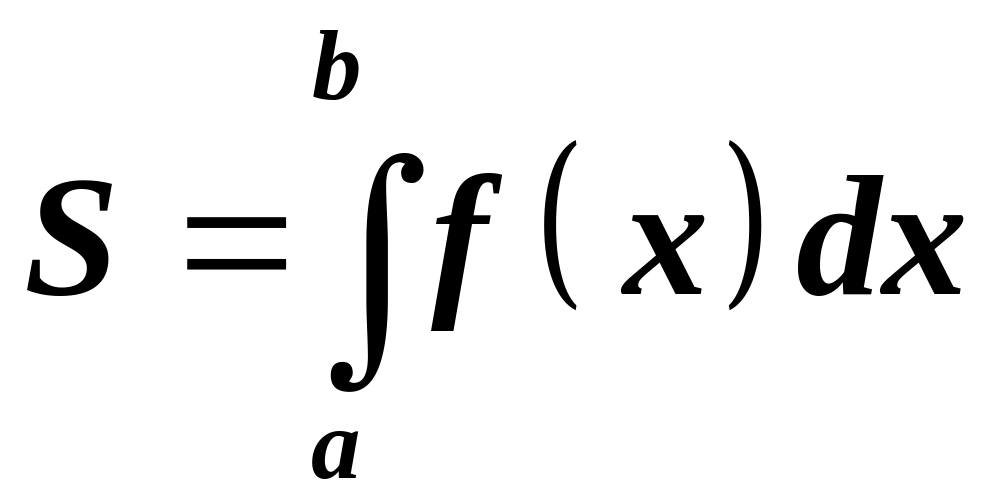(див. рис.).

В y А x b a 0

Задача 2. Знайти площу фігури, обмеженої лініями . Якщо функція неперервна на , то площа знаходиться за формулою (див. рис.).

Задача 3. Знайти площу фігури, обмеженої лініями , , , , якщо функції – неперервні та на .

Площа обчислюється за формулою: y . 0

a x b

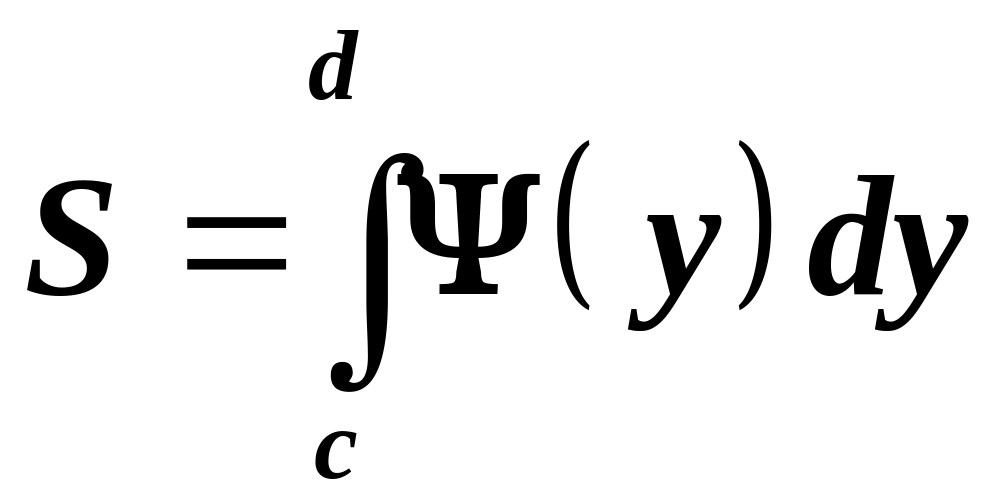Задача 4. Знайти площу фігури, обмеженої лініями , , , , якщо функція та неперервна на . Площа знаходиться за формулою: (див. рис.).

0 c d x y

У загальному випадку, щоб знайти площу плоскої фігури, її розглядають як комбінацію фігур, площі яких обчислено вище, причому інтегрування можна проводити як по одній, так і по іншій змінній.

Приклад 1. Знайти площу фігури, обмеженої лініями .

Розв’язування. Побудуємо фігуру, площу якої потрібно знайти (див. рис.):

Приклад 2. Знайти площу фігури, обмеженої лініями .

Розв’язування. Побудуємо фігуру, площу якої треба знайти:

Приклад 3. Знайти площу фігури, обмеженої графіком функції 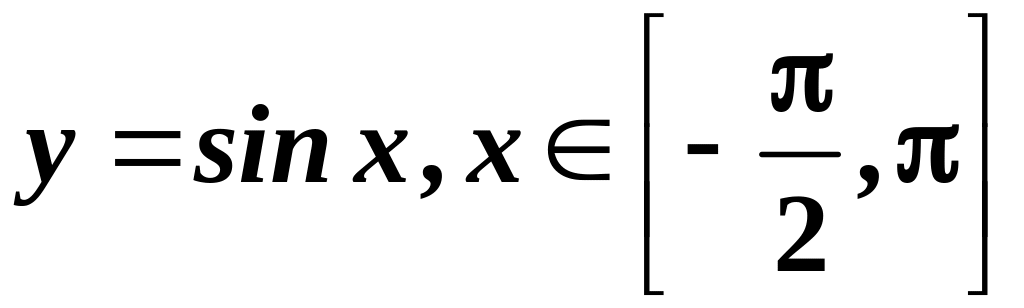та віссю абсцис.

Розв’язування. Побудуємо фігуру, площу якої треба знайти:

Розділ 3. Диференціальні рівняння

1. Основні поняття

Вивчаючи явища природи, розв’язуючи різноманітні задачі економіки, фізики, біології, природознавства та техніки, не завжди вдається безпосередньо встановити прямий зв’язок між величинами, що описують розвиток деякого процесу. Але здебільшого є можливість встановити взаємозв’язки між шуканими величинами (функціями) та швидкостями їхньої зміни відносно незалежних величин (аргументів) або між диференціалами цих змінних величин. При цьому виникають рівняння, в яких невідомі функції містяться під знаком похідної або диференціалу. Такі рівняння називають диференціальними.

Означення. Рівняння, яке зв’язує незалежну змінну, невідому функцію та її похідні (або диференціали) різних порядків, називається звичайним диференціальним рівнянням (скорочено – ДР).

Крім звичайних ДР вивчають також ДР з частинними похідними функцій кількох незалежних змінних, але ми будемо розглядати лише звичайні ДР, тому надалі назва “звичайні” не вживатиметься.

Означення. Порядком ДР називається порядок старшої похідної або диференціалу, що міститься у ДР.

У загальному вигляді ДР -го порядку можна записати наступним чином:

,

(1.1)

де - незалежна змінна (аргумент), - невідома функція аргументу , а - задана функція змінних .

Наприклад:

(1.2)

- ДР четвертого порядку;

(1.3)

- ДР третього порядку;

,	(1.4)
	(1.5)

- ДР другого порядку;

(1.6)

- ДР першого порядку.

Зауважимо, що ДР не обов’язково повинно у явному вигляді містити невідому функцію, всі її похідні та незалежну змінну. Так, наприклад, у ДР (1.2) в явному вигляді немає похідних другого і третього порядків, а також невідомої функції; у ДР (1.3) – похідної другого порядку та невідомої функції; у ДР (1.5) – незалежної змінної; у ДР (1.6) – невідомої функції. І лише ДР (1.4) містить незалежну змінну, невідому функцію та всі її похідні.

Означення. Розв’язком ДР -го порядку (1.1) називається функція , яка має неперервні похідні і разом з цими похідними задовольняє ДР (1.1), тобто перетворює його в тотожність. Якщо розв’язок задано у вигляді неявної функції , то його називають інтегралом ДР (1.1). Графік розв’язку називається інтегральною кривою.

Існує термін - зінтегрувати ДР . Це означає, що потрібно знайти ті чи інші розв’язки даного ДР (зауважимо, що при цьому необов’язково знаходяться інтеграли).

Приклад 1.1. Перевірити, що функція є розв’язком ДР

.

Розв’язування . Знаходимо похідні даної функції:

.

Підставляючи значення у ДР, дістанемо тотожність:

.

Отже, функція є розв’язком даного диференціального рівняння.

Приклад 1.2. Показати, що співвідношення (неявна функція) є інтегралом ДР

.

Розв’язування. Маємо ДР першого порядку. Застосувавши правило диференціювання СЛОЖНОЙ функції, дістанемо . Звідси . Підставивши в дане ДР, отримаємо тотожність:

.

Отже, задане співвідношення є інтегралом ДР, оскільки задає його розв’язок у вигляді неявної функції.

Приклад 1.3. Зінтегрувати ДР . Дати геометричну інтерпретацію розв’язків.

Розв’язування. Маємо так зване найпростіше ДР першого порядку . Задача знаходження розв’язків цього рівняння еквівалентна знаходженню первісних для даної функції (нагадаємо, що такі задачі розглядались нами у курсі інтегрального числення). Очевидно, що будь-яка функція вигляду

,

(1.7)

де - довільне число є розв’язком даного ДР (у цьому неважко впевнитись, підставивши у ДР і врахувавши, що , а ). Інших розв’язків це ДР не має. Дійсно, нехай - будь-який розв’язок даного рівняння, тобто . Розглянемо допоміжну функцію , де - довільна стала, і знайдемо її похідну:

Отже, функція є сталою, тобто . Звідси:

,

де - довільна стала. Оскільки, за припущенням - будь-який розв’язок даного ДР, то цим доведено, що формула (1.7) описує всі його розв’язки.

Зауваження . Виявилось, що у цьому випадку сталі - залежні, оскільки їх кількість вдалося зменшити, поклавши . А ось, наприклад, у виразі сталі - незалежні, оскільки їх неможливо об’єднати в одну довільну сталу.

Знайдемо декілька розв’язків вихідного ДР і побудуємо відповідні інтегральні криві. При дістаємо розв’язок , графіком якого (інтегральною кривою) є пряма - бісектриса першого та третього координатних кутів. При інших значеннях дістаємо інші розв’язки, яким відповідають інтегральні криві - прямі, паралельні цій бісектрисі. Множина всіх розв’язків має ту властивість, що відповідна сім’я інтегральних кривих покриває всю площину, причому через кожну точку площини проходить єдина інтегральна крива (див. Рис. 1, на якому побудовано декілька інтегральних кривих).

Рис. 1.

Приклад 1.3 показує, що ДР може мати безліч розв’язків (у даному прикладі – це безліч функцій вигляду (1.7), які залежать від довільного параметру ).

Взагалі кажучи, для пошуку розв’язків ДР -го порядку (1.1) потрібно буде послідовних інтегрувань. Розв’язок загального вигляду (тобто, співвідношення, яке описує всі розв’язки) буде залежати від довільних сталих, причому ці довільні сталі – незалежні. Останнє означає, що будь-яку із цих сталих не можна виразити через інші, тобто кількість незалежних довільних сталих зменшити неможливо, і ця кількість дорівнює порядку ДР.

Означення . Загальним розв’язком ДР -го порядку (1.1) називається функція

,

яка залежить від аргументу та від незалежних довільних сталих і яка задовольняє умовам:

1. має неперервні похідні ;

2. при будь-яких значеннях сталих вона є розв’язком ДР;

3. будь-який розв’язок (за винятком, можливо, особливого, поняття про який буде розглянуто нижче) можна дістати із цієї функції при певних значеннях сталих .

Означення . Загальним інтегралом ДР -го порядку (1.1) називають його загальний розв’язок, заданий у вигляді неявної функції:

.

Означення . Частинним розв’язком ( частинним інтегралом ) ДР (1.1) називається його розв’язок, який одержується із загального розв’язку (або із загального інтегралу ), якщо надати довільним сталим певних числових значень.

Зауважимо, що поняття розв’язку та частинного розв’язку, як правило, не розрізняють.

Приклад 1.4. Показати, що функція , де - довільна стала є розв’язком ДР . Чи буде цей розв’язок загальним ?

Розв’язування. Знаходимо похідні:

.

Підставляючи значення похідних у ДР, отримаємо тотожність:

Таким чином, ми показали, що функція є розв’язком ДР при будь-якому значенні сталої . Але цей розв’язок не буде загальним, оскільки він містить лише одну довільну сталу, а дане рівняння є ДР третього порядку.

Приклад 1.5. Знайти загальний та декілька частинних розв’язків ДР

.

Розв’язування. Маємо найпростіше ДР другого порядку, яке розв’язується послідовними інтегруваннями. Знайдемо спочатку похідну першого порядку (яка є первісною для ), зінтегрувавши , тобто:

,

де - довільна стала, а символом тут і надалі будемо позначати будь-яку первісну для функції . Отже:

.

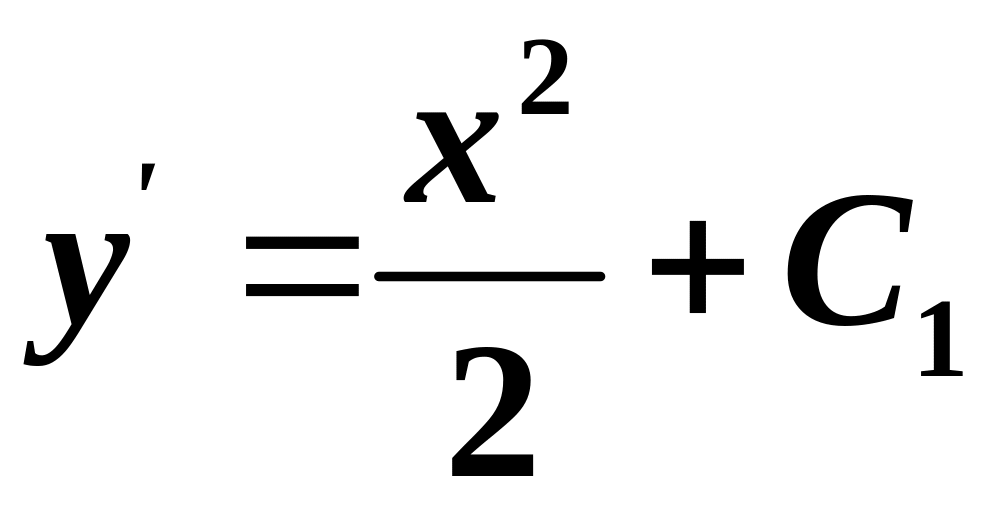Аналогічно знаходимо , інтегруючи :

,

де - довільна стала.

Таким чином, одержуємо:

.

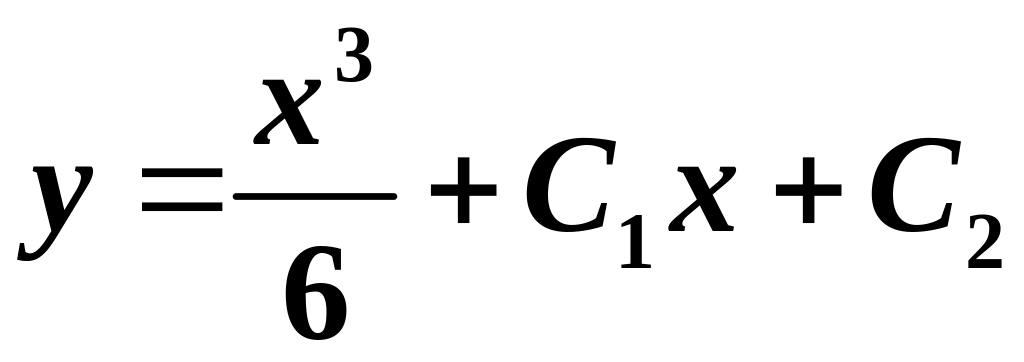Ця функція містить дві незалежні довільні сталі і є загальним розв’язком даного ДР другого порядку.

Знайдемо декілька частинних розв’язків. Покладаючи , дістанемо частинний розв’язок . Якщо , то відповідний розв’язок: 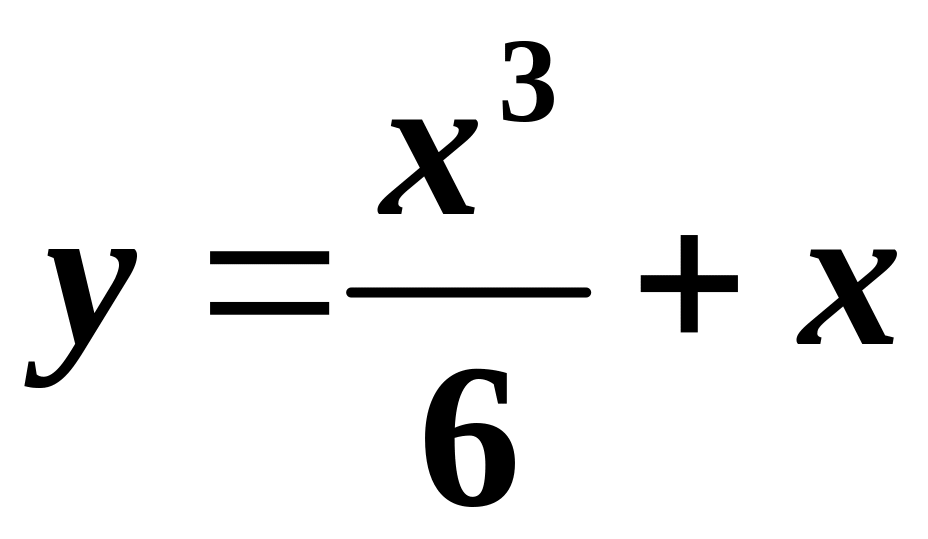. При маємо частинний розв’язок .

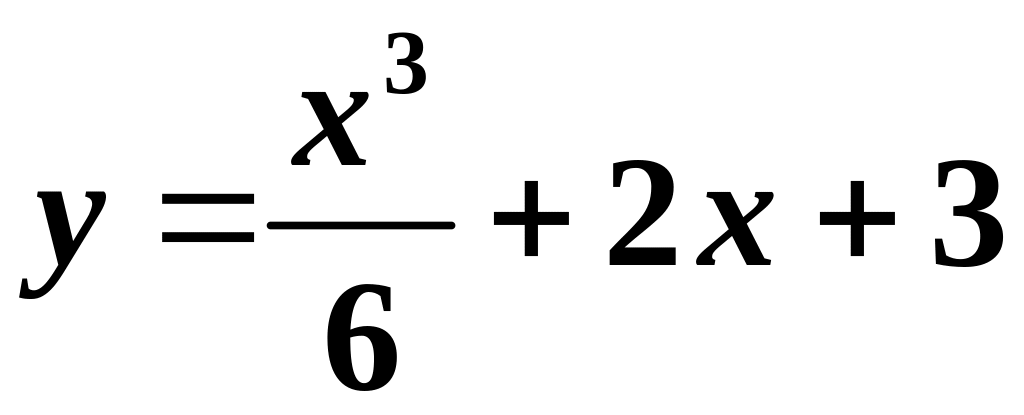Очевидно, що частинних розв’язків безліч. Кожний частинний розв’язок, отриманий із загального розв’язку, задовольняє даному ДР.

Підкреслимо, що раніше, у шкільному курсі елементарної математики, ми мали справу з алгебраїчними або тригонометричними рівняннями, розв’язками яких були деякі числові множини. На відміну від них диференціальні рівняння мають своїми розв’язками функції або навіть множини функцій.

Нижче основні поняття будуть більш детально розглянуті на прикладі ДР першого порядку.