Екстремуми функції двох змінних.

Означення. Точка називається точкою максимуму (мінімуму) функції , якщо існує окіл точки , що для всіх точок , які належать цьому околу і відмінних від , виконується умова

Точки максимуму і мінімуму функції називаються точками екстремуму.

Означення. Точки з області визначення функції, в яких усі частинні похідні першого порядку дорівнюють нулю або не існують, називаються критичними точками.

Означення. Ті точки, в яких усі частинні похідні першого порядку існують і дорівнюють нулю, називаються стаціонарними.

В цих точках вектор-градієнт є нуль-вектор. Іншими словами: повний диференціал першого порядку у стаціонарних точках тотожно (при будь-яких приростах аргументів) дорівнює нулю.

Теорема (необхідна умова екстремуму функції).

Якщо функція у точці досягає екстремуму, то ця точка є критичною.

Із теореми випливає, що екстремуми слід шукати лише серед критичних точок (які можна назвати підозрілими на екстремуми).

Зауваження. Кожна точка екстремуму є критичною, але не кожна критична точка є точкою екстремуму.

Приклад . .

; ;

– критична точка і . Але вона не є точкою екстремуму, оскільки , якщо (тобто, і мають однаковий знак), і , якщо (тобто і мають різні знаки).

Для з’ясування питання про існування екстремуму функції у критичній точці потрібно знайти у цій точці диференціал другого порядку і дослідити його знак при довільних приростах аргументів. Якщо , то - точка мінімума, а якщо , то - точка максимума (порівняй із другою достатньою умовою екстремума для функції одного аргумента, так званим «правилом дощу»). Але якщо для функції одного аргумента і знак диференціала другого порядку співпадає зі знаком другої похідної, то для функцій двох і більше аргументів це не так. Тому використовують достатню умову, яка базується на дослідженні диференціалу другого порядку як квадратичної форми відносно приростів аргументів (а саме – на основі додатної або від’ємної визначеності цієї форми).

Теорема (достатня умова екстремуму). Нехай у деякому околі стаціонарної точки функція має неперервні частинні похідні другого порядку.

Розглянемо визначник Гессе (Гессіан) у цій точці.

.

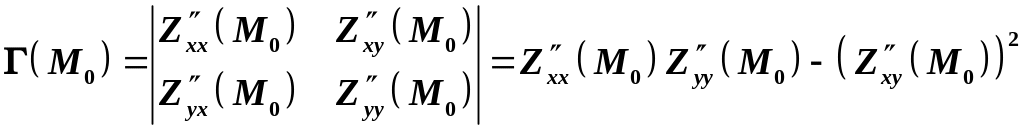1. Якщо 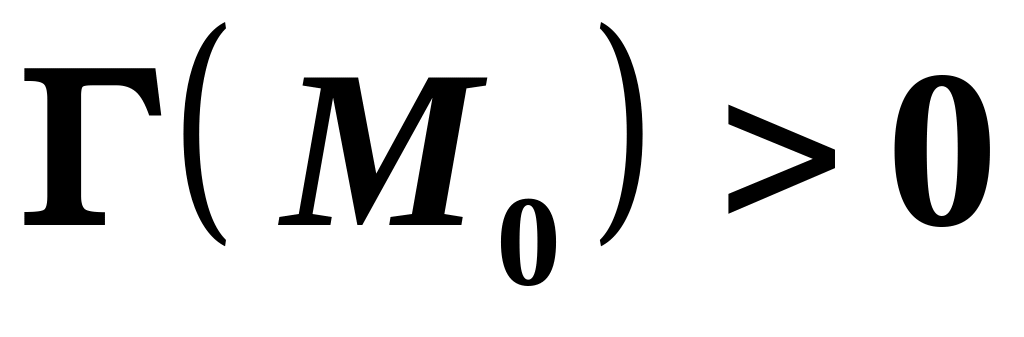, то - точка екстремуму, причому: якщо , то – точка мінімуму; якщо , то – точка максимуму.

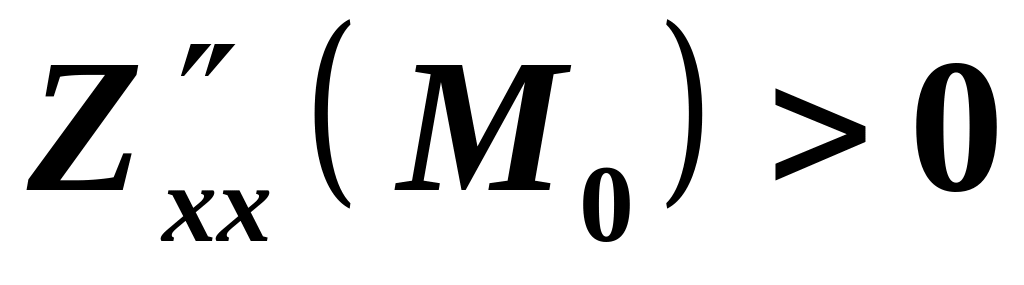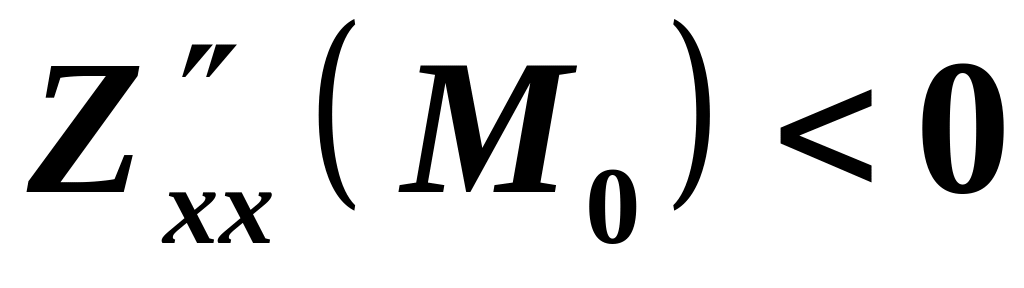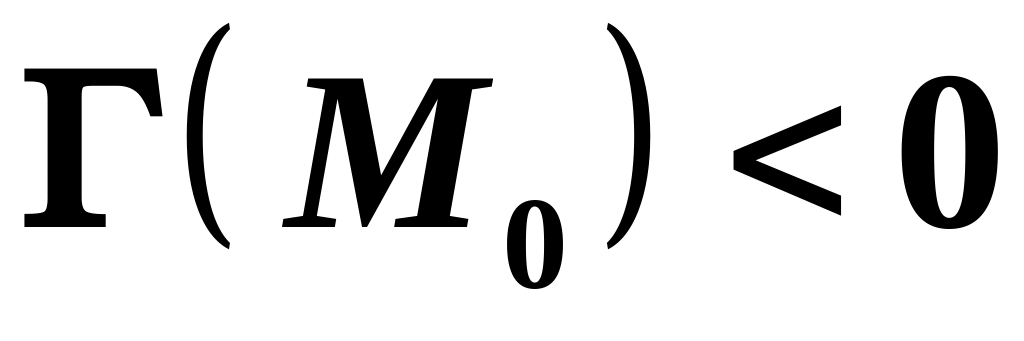2. Якщо , то в точці екстремуму немає.

3. Якщо , то питання про існування екстремуму залишається відкритим і потрібні додаткові досліждення.

Зауваження 1. Очевидно, що коли , то

,

тобто, і мають однакові знаки, тому визначити вид екстремуму ( або ) можна і за знаком .

Зауваження 2. Очевидно, що коли , то умова а) еквівалентна додатності диференціала другого порядку, тобто , а умова б) еквівалентна від’ємності диференціала другого порядку, тобто .

Приклад . Дослідити на екстремум функцію: .

Розв’язування.

Область визначення функції .

Знайдемо частинні похідні першого порядку:

, .

Оскільки похідні визначені на , то серед критичних будуть лише стаціонарні точки. Знайдемо їх, розв’язуючи систему рівнянь:

.

Маємо дві стаціонарні точки і - підозрілі на екстремум (за теоремою – необхідна умова екстремуму). Застосуємо теорему - достатню умову існування екстремуму. Для цього знайдемо частинні похідні другого порядку:

; ; .

Вираз для Гессіана має наступний вигляд:

.

- точка екстремуму.

Оскільки – точка мінімуму.

в точці екстремуму немає.

Відповідь: .

Приклад . Дослідити на екстремум функцію: .

Розв’язування.

; частинні похідні першого порядку: , визначені у будь-якій точці координатної площини, тому серед критичних будуть лише стаціонарні точки. Знайдемо їх, розв’язуючи систему рівнянь:

стаціонарна точка – підозріла на екстремум (за теоремою – необхідна умова екстремуму). Застосуємо теорему - достатню умову існування екстремуму. Для цього знайдемо частинні похідні другого порядку:

; ; .

Вираз для Гессіана: .

за теоремою питання про екстремум в точці відкрите. Але в точці функція досягає мінімума , оскільки очевидно, що для всіх точок .

Приклад . Дослідити на екстремум функцію: .

Розв’язування.

; частинні похідні першого порядку ; визначені у будь-якій точці координатної площини, тому серед критичних будуть лише стаціонарні точки. Знайдемо їх, розв’язуючи систему рівнянь:

стаціонарна точка – підозріла на екстремум (за теоремою – необхідна умова екстремуму). Застосуємо теорему - достатню умову існування екстремуму. Для цього знайдемо частинні похідні другого порядку:

; ; .

Вираз для Гессіана: .

за теоремою питання про екстремум в точці відкрите. Додаткові дослідження показують, що для всіх точок площини з від’ємними координатами , а для всіх точок площини з додатними координатами в точці екстремуму немає.