2. Диференціальні рівняння першого порядку

Означення. ДР першого порядку називається співвідношення вигляду:

,

(2.1)

або рівняння:

,

(2.2)

яке називають ДР першого порядку, розв’язаним відносно похідної (зауважимо, що інколи вдається ДР (2.1) звести до вигляду (2.2), а іноді й ні). Тут -незалежна змінна (аргумент), - невідома (шукана) функція аргументу , - її похідна, а , - задані цілком визначені функції, що задовольняють певним умовам.

Часто використовують симетричну форму запису ДР першого порядку:

,

де - задані функції змінних та (підкреслимо, що у цьому випадку незалежною змінною можна вважати як так і ).

Переформулюємо та конкретизуємо основні поняття із попереднього пункту 1. для випадку ДР першого порядку, а також розглянемо деякі нові означення. При цьому, якщо це спеціально не обумовлено, всюди надалі будемо вважати, що всі змінні та функції розглядаються на області визначення відповідних ДР.

Означення . Розв’язком ДР першого порядку (2.1) (або (2.2) ) називається неперервно диференційовна функція , яка перетворює це рівняння в тотожність, тобто

, ( або ) .

Співвідношення називається інтегралом ДР (2.1) або (2.2), якщо воно неявно задає розв’язок відповідного диференціального рівняння.

Означення . Графік розв’язку називається інтегральною кривою ДР.

Означення . Через кожну точку області визначення ДР (2.2) проведемо інтегральну криву і дотичну до неї, тангенс кута нахилу якої до осі абсцис дорівнює . Ця множина дотичних (інколи замість дотичних беруть їх одиничні напрямні вектори) називається полем напрямків ДР (2.2), або полем напрямків функції .

Інтегральна крива в кожній своїй точці дотикається до поля напрямків функції . Крива, яка в кожній своїй точці дотикається до напрямку, що є в цій точці, є інтегральною кривою.

Означення. Ізокліною називають лінію, в кожній точці якої напрямок поля однаковий. Усі інтегральні криві, які перетинають дану ізокліну, утворюють з віссю абсцис один і той самий кут.

Зауважимо, що за допомогою ізоклін (які визначаються рівняннями ) іноді вдається наближено побудувати інтегральні криві.

Загальний розв’язок ДР першого порядку має вигляд (порівняй із виглядом загального розв’язку ДР -го порядку у пункті 1.):

,

(2.3)

а загальний інтеграл:

,

(2.4)

де - довільна стала.

Графіком загального розв’язку (загального інтегралу) є однопараметрична сім’я інтегральних кривих, яких безліч (оскільки стала приймає довільні значення). Із прикладів, наведених у попередньому пункті, видно, що мати своїми розв’язками множину функцій – характерна особливість ДР. Розв’язавши ДР, яке описує перебіг певного процесу, дістанемо множину залежностей між величинами, що характеризують цей процес. І для того, щоб вибрати із множини залежностей ту одну, яка притаманна саме цьому процесу, треба мати якусь додаткову інформацію, наприклад, знати початковий стан процесу.

Отже, для того, щоб дістати із загального розв’язку (2.3) частинний розв’язок ДР першого порядку, потрібно задати значення , яке шукана функція набуває при певному значенні аргументу , тобто потрібно мати, як прийнято казати, початкову умову при . Якщо підставити значення та у рівність (2.3), то отримаємо рівняння із однією невідомою : . Розв’язуючи це рівняння, знайдемо відповідне значення . Знайдене значення підставимо у рівність (2.3) і дістанемо частинний розв’язок , який задовольняє дану початкову умову. Аналогічно, розв’язуючи рівняння , знаходиться частинний інтеграл із загального інтегралу.

Означення . Задачу знаходження частинного розв’язку ДР першого порядку, який задовольняє початкову умову (або ), називають задачею Коші для цього ДР.

Зауважимо, що розв’язок ДР (2.2) існує не для всіх функцій і не при будь-яких початкових умовах. Але є достатні умови існування таких розв’язків. Наприклад, справедлива наступна

Теорема Коші . Якщо у ДР першого порядку функція та її частинна похідна неперервні в деякій замкненій області площини і точка , тоді існує єдиний розв’язок цього ДР, який задовольняє початкову умову при .

Геометричний зміст теореми Коші полягає в тому, що графік розв’язку , тобто інтегральна крива, яка проходить через точку , єдина.

Якщо в точці умови теореми Коші виконуються, то початкову умову називають допустимою або точкою єдиності розв’язку задачі Коші. Якщо ж через цю точку проходить більше ніж одна інтегральна крива (або жодної інтегральної кривої), то таку точку називають особливою. Особливі точки можуть бути ізольованими або заповнювати цілу лінію, яку у цьому випадку називають особливою інтегральною кривою, а розв’язок, який відповідає цій інтегральній кривій - особливим розв’язком.

Можна уточнити означення загального розв’язку.

Означення . Загальним розв’язком ДР першого порядку (2.2) називається такий його розв’язок, що залежить від однієї довільної сталої , з якого можна дістати будь-який частинний розв’язок, що відповідає допустимій умові теореми Коші.

Зауважимо, що можуть бути розв’язки ДР, які неможливо отримати із загального розв’язку (тобто, особливі розв’язки).

Приклад 2.1. Показати, що функція

,

(2.5)

де - довільна стала, є загальним розв’язком ДР

.

Розв’язування. Маємо ДР першого порядку у симетричній формі.Підставляючи функцію (2.5) в ліву частину рівняння і враховуючи, що , дістаємо:

.

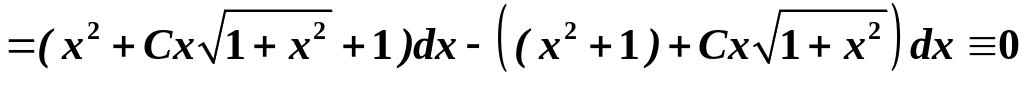Отже, при будь-якому функція (2.5) є розв’язком даного ДР.

Доведемо, що будь-який розв’язок рівняння можна дістати з (2.5) при певному значенні сталої . Припустимо, що - деякий розв’язок нашого ДР . Тоді маємо тотожність:

.

(2.6)

Розглянемо допоміжну функцію 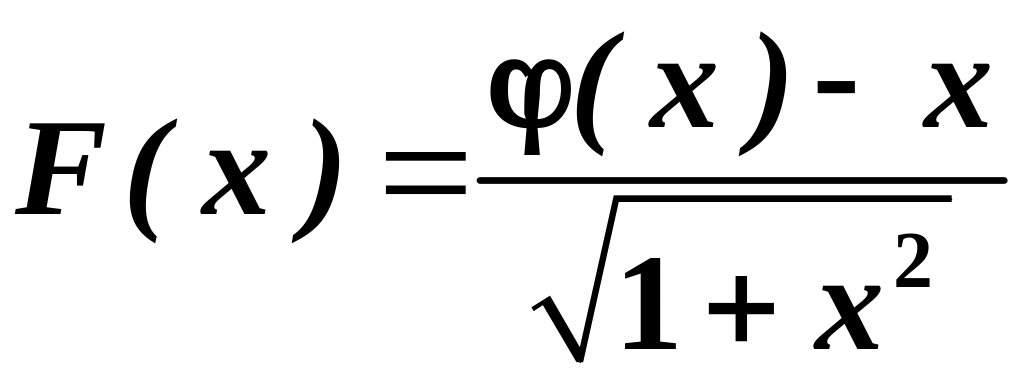. Її похідна:

,

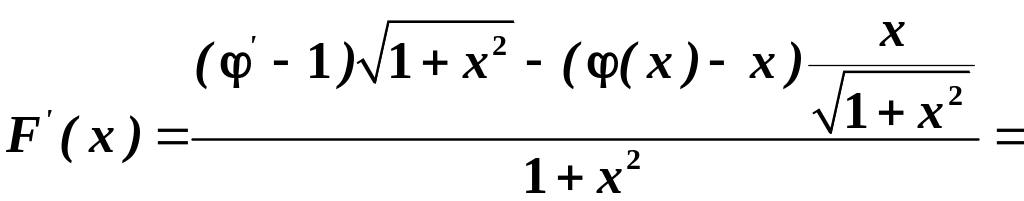
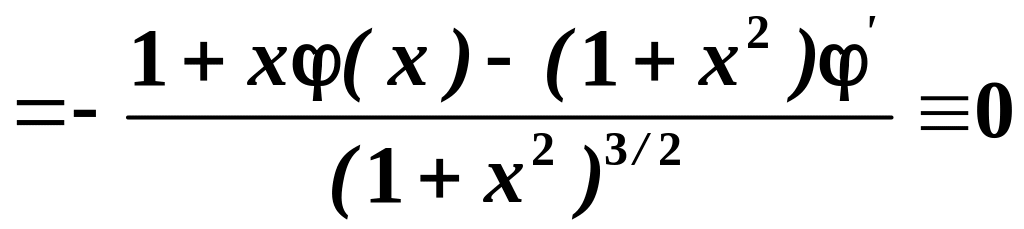внаслідок рівності (2.6) . Звідси випливає, що , де - дійсне число, тобто:

.

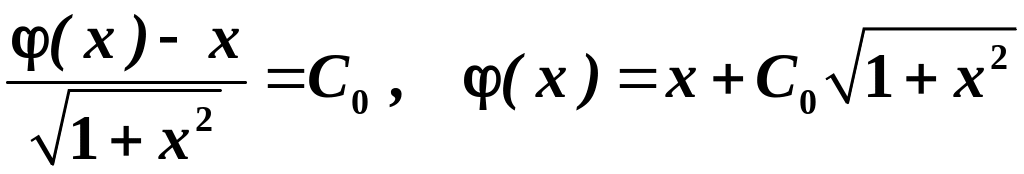Таким чином, розв’язок можна дістати з формули (2.5) при . Отже, функція (2.5) є загальним розв’язком даного ДР.

Приклад 2.2. Показати, що функція 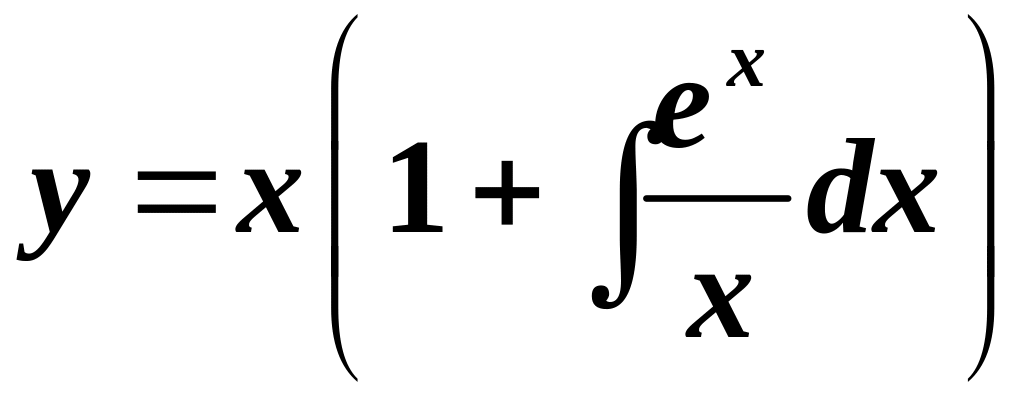є розв’язком рівняння .

Розв’язування. Маємо ДР першого порядку вигляду (2.1). Спочатку знайдемо похідну даної фунції (нагадаємо, що похідна від невизначеного інтегралу дорівнює підінтегральній функції):

Підставивши та у ліву частину ДР, дістанемо:

.

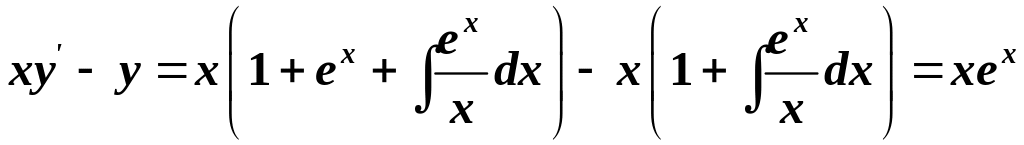Дана функція перетворює ДР в тотожність і, отже, є розв’язком ДР.

Зауваження. В деяких випадках розв’язки ДР не виражаються через елементарні функції (як у прикладі 2.2), або ці розв’язки не вдається знайти. Тоді застосовують наближені методи розв’язування, але при цьому важливо знати, що розв’язки ДР існують.

Приклад 2.3. Для ДР а) та б) знайти загальні розв’язки, дати їх геометричну ілюстрацію, якщо ж задано початкову умову, то вказати відповідну інтегральну криву:

а) , ;

б) .

Розв’язування. а). Неважко впевнитись, що загальний розв’язок даного найпростішого ДР першого порядку задається формулою:

,

(2.7)

де - первісна для функції , а - довільна стала. При кожному значенні із загального розв’язку (2.7) дістаємо частинний розв’язок, графіком якого (інтегральною кривою) є парабола. Множина всіх розв’язків (загальний розв’язок) має ту властивість, що відповідна сім’я інтегральних кривих (парабол) покриває всю площину, причому через кожну точку площини проходить єдина інтегральна крива.

Дійсно, у будь-якій точці координатної площини функція та її частинна похідна неперервні, тобто умови теореми Коші виконуються для всіх точок площини.

На Рис.2.а) побудовано три параболи (інтегральні криві), що визначаються функцією (2.7) і проходять через точки , тобто зображають графіки частинних розв’язків, які отримуються із загального розв’язку (2.7) відповідно при .

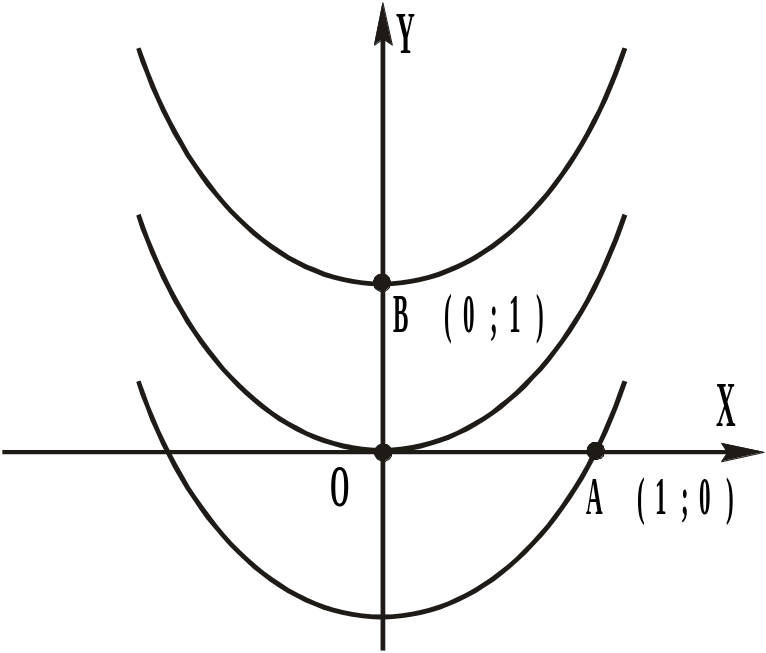
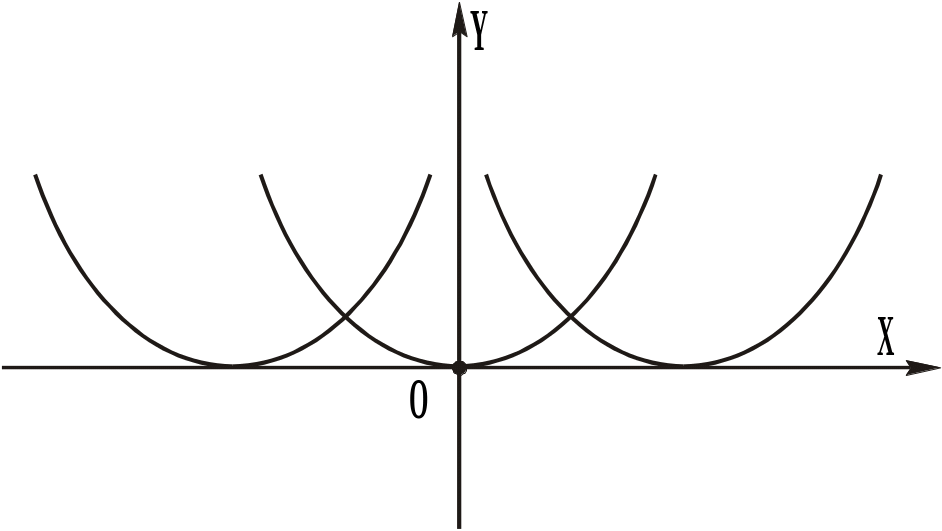
а)

б)

Рис. 2.

Частинному розв’язку , що задовольняє початкову умову , тобто розв’язку задачі Коші для даного ДР, відповідає інтегральна крива (парабола), яка проходить через точку .

б).Маємо так зване ДР з відокремлюваними змінними. Враховуючи, що , приведемо дане ДР до вигляду:

.

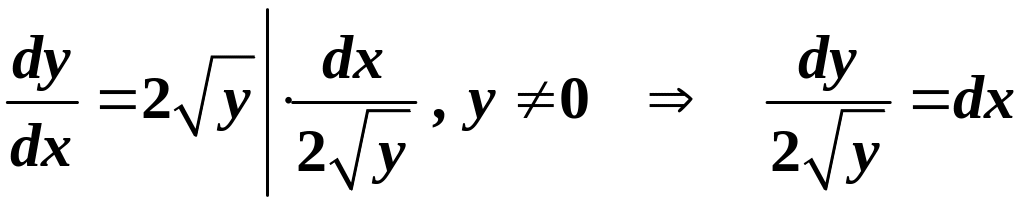Інтегруючи ліву частину отриманої рівності по (будемо вважати, що зроблено заміну змінних ), а праву по , знаходимо загальний інтеграл:

.

Звідси дістаємо загальний розв’язок:

.

Графіками цих функцій (інтегральними кривими) є сім’я парабол (див. Рис. 2.б)). НЕВЕРНО НЕВЕРНО НЕВЕРНО

Зауважимо, що у даного ДР є очевидний розв’язок , який неможливо отримати із загального розв’язку (або із загального інтегралу) ані при яких значеннях . Це - особливий розв’язок, тому що через кожну точку інтегральної лінії (осі абсцис) проходить ще одна інтегральна крива - парабола. У цьому випадку порушується умова неперервності частинної похідної 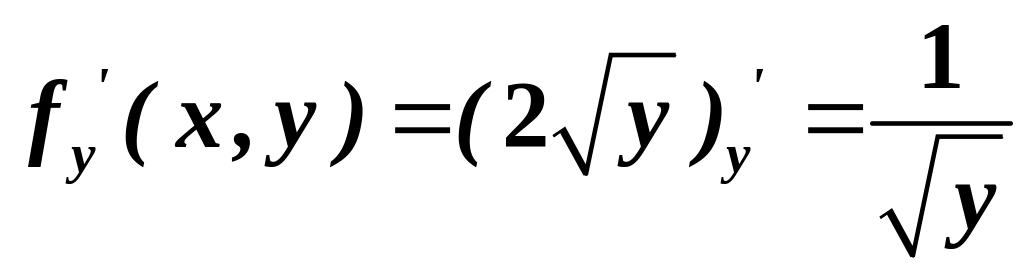у кожній точці осі абсцис.