Визначений інтеграл Задача про площу криволінійної трапеції.

Фігура, обмежена відрізком осі , двома прямими і , і графіком неперервної функції , яка набуває невід’ємних значень, називається криволінійною трапецією.

Знайдемо площу цієї фігури.

Основу криволінійної трапеції (відрізок ) розіб’ємо на довільних частин точками . Площа криволінійної трапеції буде дорівнювати сумі площ частинних криволінійних трапецій: .

На кожному частинному відрізку довжиною виберемо довільну точку і побудуємо прямокутник із основою і висотою . Площа кожного такого прямокутника дорівнює і . Складемо суму: , яку назвемо інтегральною сумою.

Очевидно, що 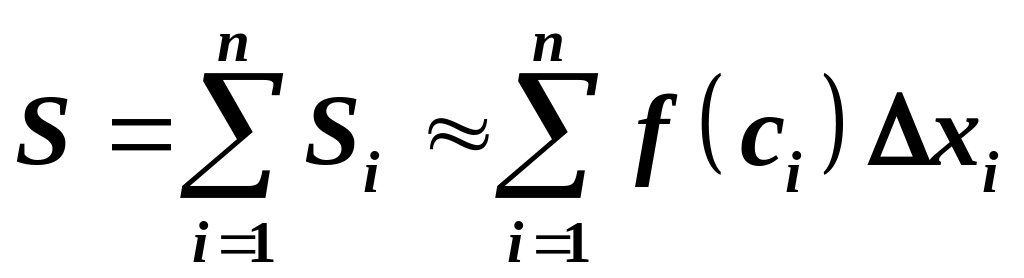і можна скласти скільки завгодно таких сум, які, можливо, будуть залежати як від способу розбиття відрізка на частинні, так і від вибору проміжних точок . Довжину найбільшого частинного відрізка позначимо через .

Означення. Якщо границя інтегральних сум 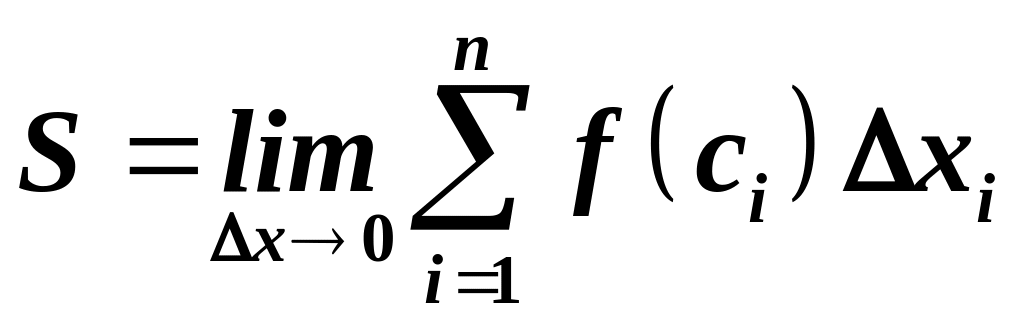існує, скінчена і не залежить від способу розбиття відрізка на частинні відрізки, а також від вибору проміжних точок , то ця границя називається площею криволінійної трапеції.

Поняття визначеного інтеграла.

Нехай функція неперервна на сегменті , який розіб’ємо на частинних сегментів: . На кожному частинному відрізку візьмемо довільну точку і складемо інтегральну суму 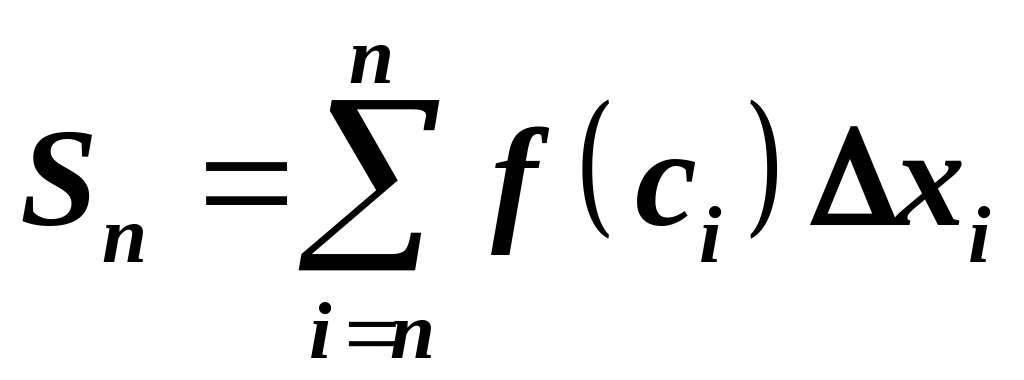. Позначимо: .

Означення. Якщо границя інтегральних сум існує, скінчена і не залежить від способу розбиття сегмента на частинні відрізки, а також від вибору проміжних точок , то ця границя називається називається визначеним інтегралом функції на проміжку і позначається:

.

Числа і називаються нижньою і верхньою межами інтегрування відповідно. При цьому відрізок називається проміжком інтегрування, а –змінною інтегрування.

Теорема (існування визначеного інтеграла). Якщо функція неперервна на відрізку , то вона на цьому відрізку має визначений інтеграл (або кажуть, що функція інтегровна на ).

Геометричний зміст визначеного інтеграла. Якщо – неперервна і невід’ємна на функція, то з геометричної точки зору, визначений інтеграл дорівнює площі криволінійної трапеції, обмеженої графіком функції , відрізком осі та прямими і .

Зв’язок між визначеним і невизначеним інтегралом встановлює формула Ньютона–Лейбніца.

Теорема Ньютона–Лейбніца. Якщо функція неперервна на відрізку і довільна первісна для функції на цьому відрізку, то визначений інтеграл функції на дорівнює подвійній підстановці від первісної:

.

По іншому: .

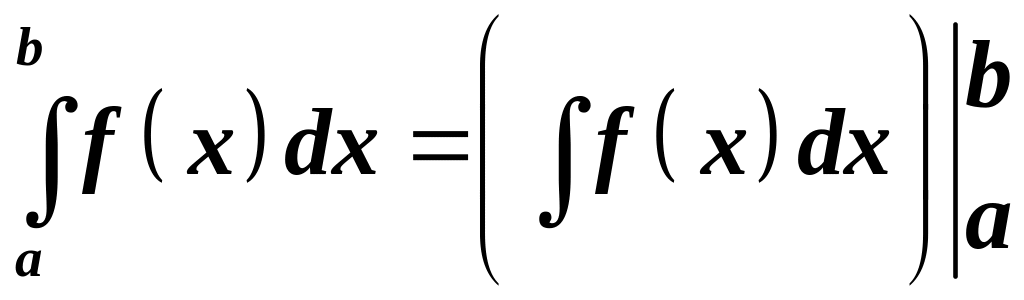Обернений зв’язок між визначеним та невизначеним інтегралами встановлює наступна

Теорема про інтеграл зі змінною верхньою межею. Нехай функція неперервна на будь-якому відрізку . Тоді визначений інтеграл 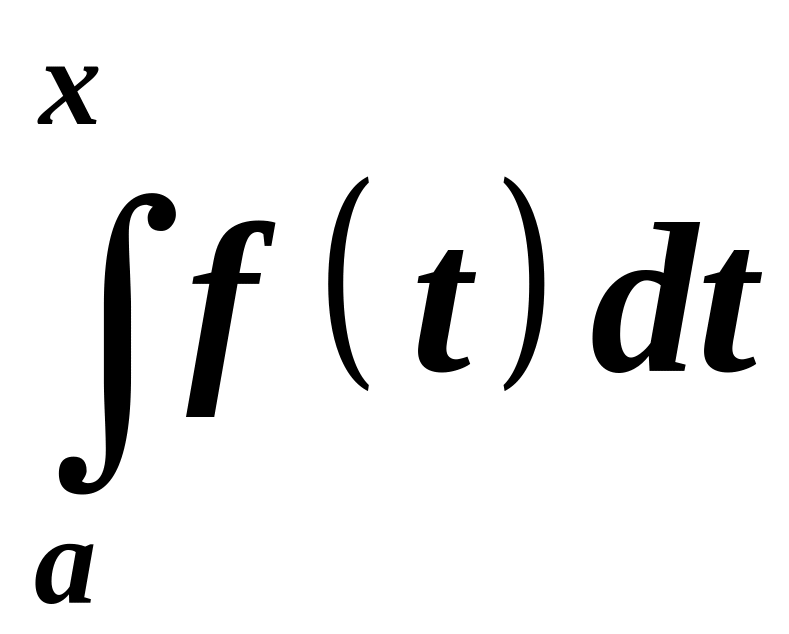задає деяку функцію 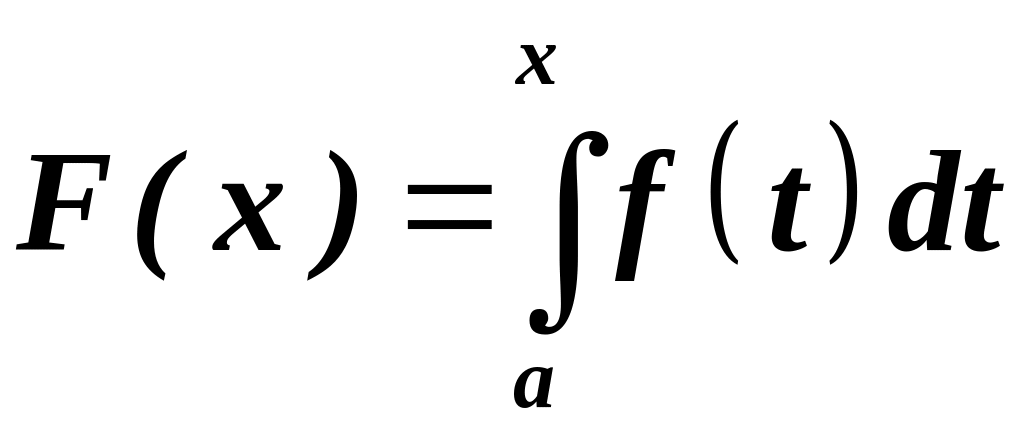. Похідна від інтеграла зі змінною верхньою межею дорівнює підінтегральній функції (із заміною змінної інтегрування на верхню межу):

.

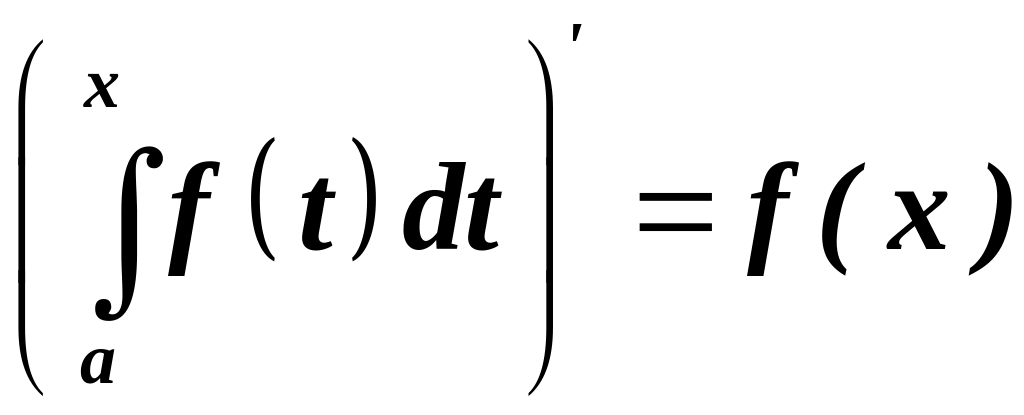Іншими словами, інтеграл зі змінною верхньою межею дорівнює первісній для підінтегральної функції.

Доведення. За теоремою Ньютона-Лейбніца:

.
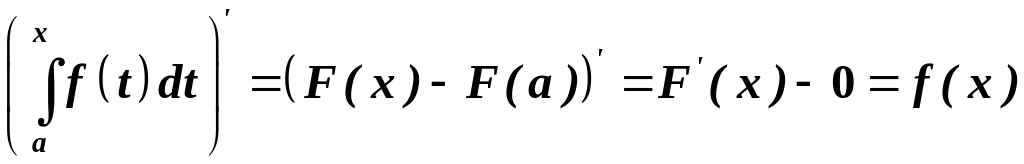