Основні поняття.

У багатьох задачах економіки доводиться моделювати залежності результату від впливу на нього декількох (більше одного) факторів. Це призводить до необхідності вивчення функцій декількох незалежних змінних вигляду . Для спрощення і можливості геометричної інтерпретації (не втрачаючи при цьому загальності) всюди надалі розглядаються лише функції двох змінних або .

Означення. Якщо кожній точці за деяким законом або правилом поставлено у відповідність єдине число , то кажуть, що задано функцію двох незалежних змінних або .

При цьому множина називається областю визначення функції, а множина – множиною значень функції.

Якщо не задана, то область визначення аналітично заданої функції двох змінних є множина точок простору , при яких аналітичний вираз має сенс.

Розглянемо деякі приклади знаходження областей визначення функцій двох змінних. При цьому для наочності будемо знаходити геометричні образи областей визначення.

у х 0 Приклад . Знайти область визначення функції . Розв’язування. оскільки аналітичний вираз має сенс, коли його знаменник не дорівнює нулю. Геометричний образ – множина усіх точок площини , окрім точок прямої (див.рис).
у х 0 Приклад . Знайти область визначення функції . Розв’язування. , оскільки аналітичний вираз має сенс, коли аргумент логарифма додатний. Геометричний образ - це множина точок площини , координати яких мають однаковий знак (І і ІІІ координатні чверті), окрім точок, які належать осям і .

У подальшому, при знаходженні геометричних образів розв’язків нерівностей з двома змінними та їх систем будемо використовувати наступне правило, яке базується на властивості збереження знаку неперервною функцією.

Правило («метод пробної точки»). Нехай у площині задана лінія , яка визначається рівнянням (де - неперервна функція), і ця лінія розбиває площину на дві області: та . Якщо у довільній точці , що належить одній із цих областей, виконується нерівність ( ), то вона виконується в усіх точках цієї області.

Приклад . Знайти область визначення функції .

Розв’язування.

.

Для знаходження геометричного образа області визначення розглянемо рівняння границі :

, або .

2 у х 0 2 Це рівняння кола з центром у точці і радіуса . Дане коло поділяє всю координатну площину на дві частини: внутрішню (усередині кола) і зовнішню (поза ним). “Методом пробної точки” визначаємо потрібну частину площини: наприклад, координати точки , яка лежить усередині кола, задовольняють нерівність .

За вказаним правилом ця нерівність буде виконуватись для всіх точок площини, які лежать усередині кола. Отже, областю визначення функції є круг разом із границею - колом.

У попередніх прикладах функція двох змінних була задана аналітично (формулою), але її також можна задати таблично, графічно тощо.

Наприклад, залежність об’єму виробництва від двох основних факторів виробництва – капіталу і – праці – можна зобразити у вигляді таблиці, де для кожного набору витрат капіталу і витрат праці можна знайти відповідний об’єм виробництва :

…	…	…	…	…

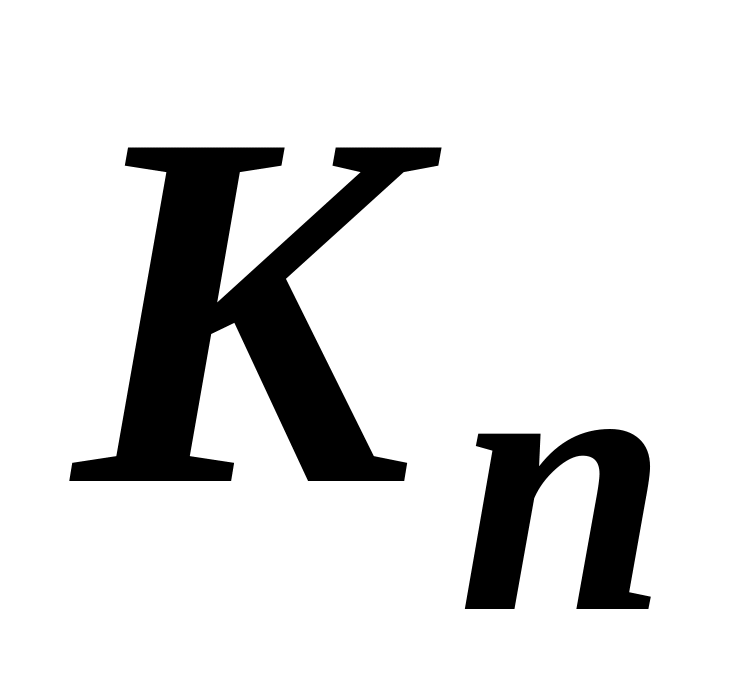
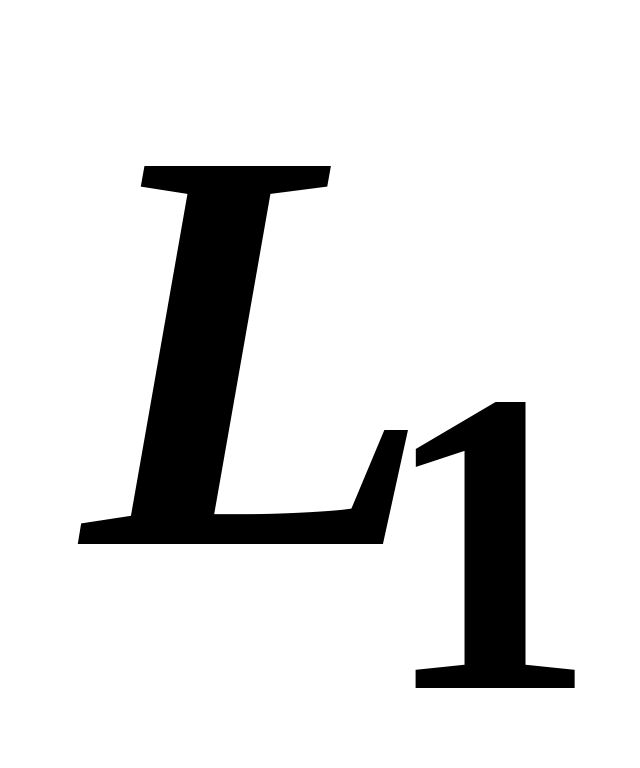
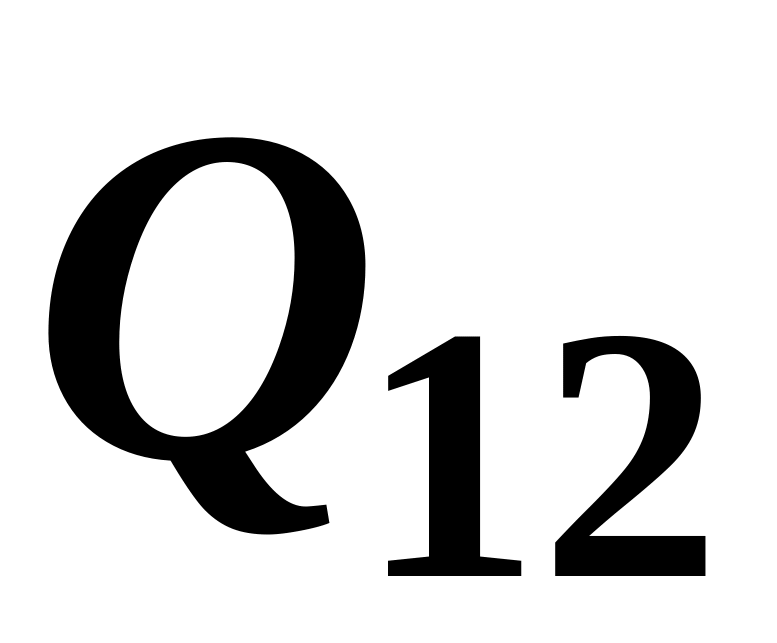
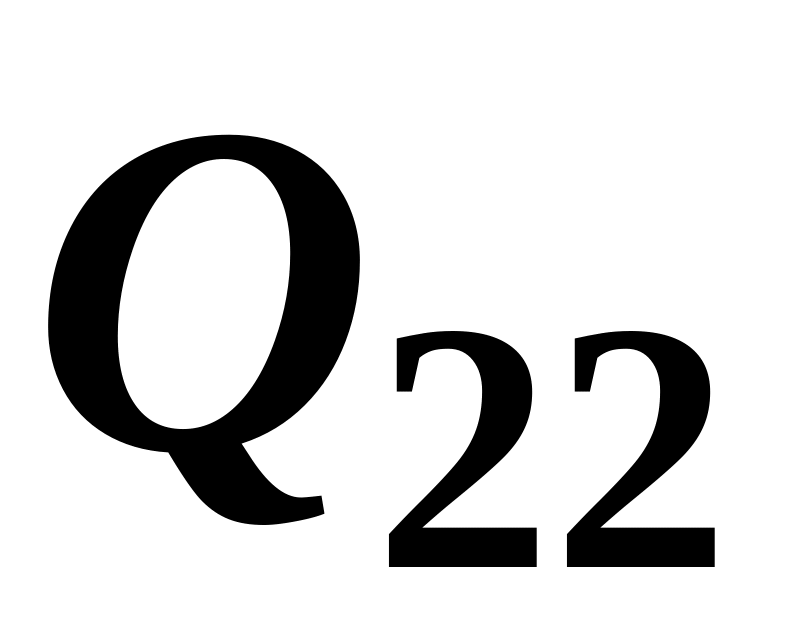
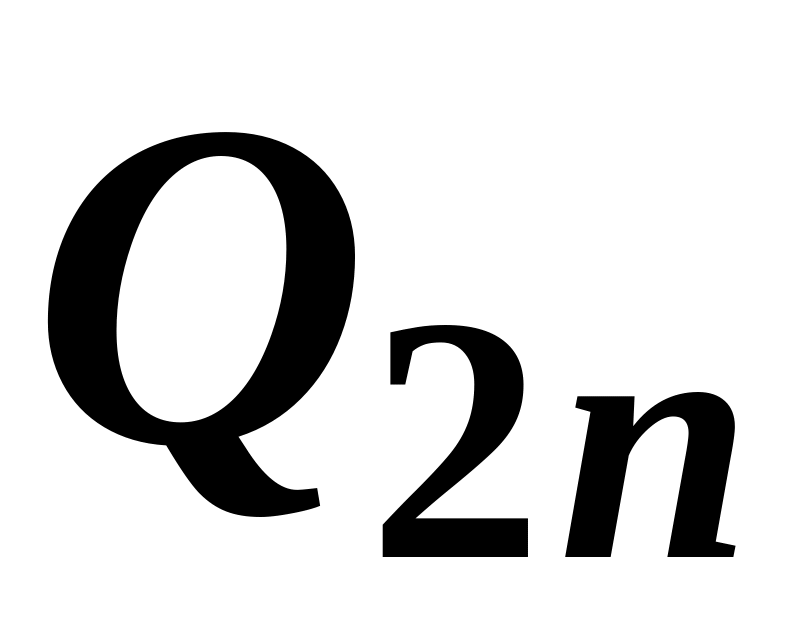
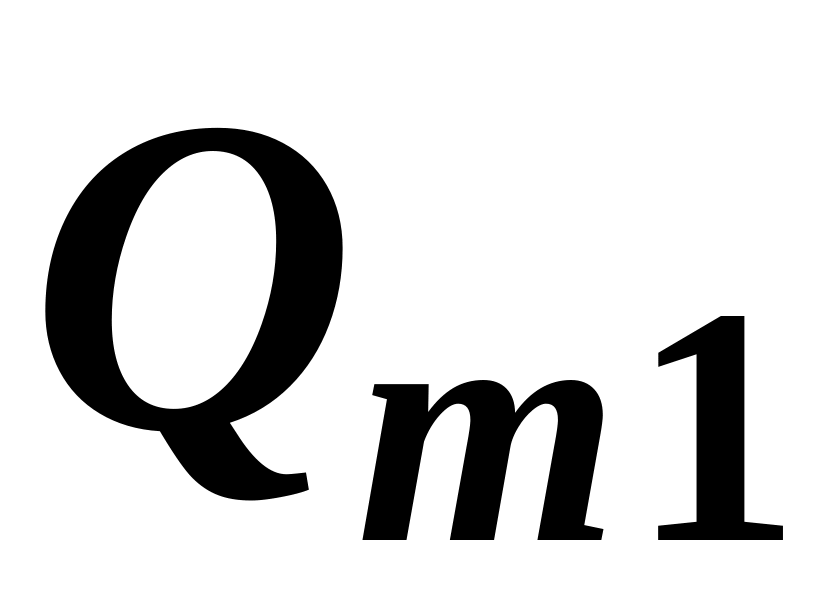
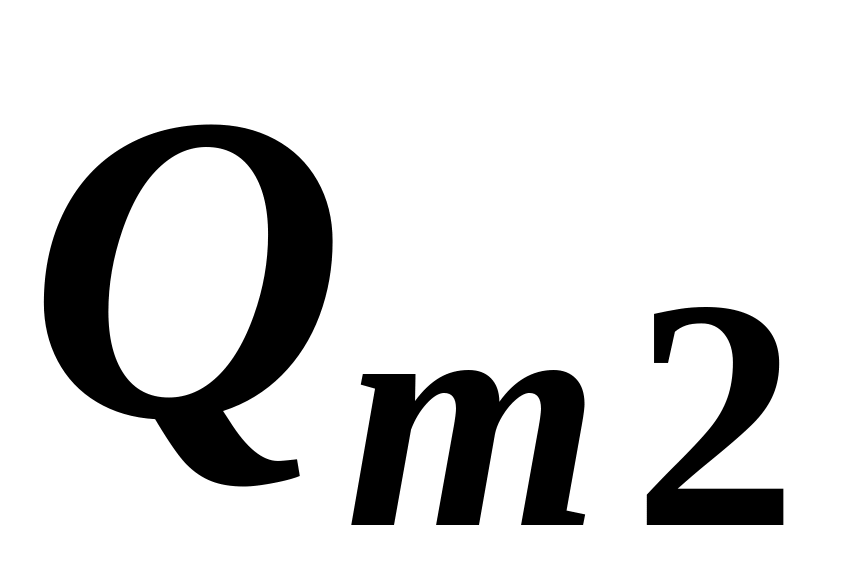
Графіком функції двох змінних називається множина точок простору . Ця множина, як правило, утворює деяку поверхню у трьохвимірному просторі.

Приклади.

x z y 0

Графіком функції є площина, яка перетинає осі координат у точках .

Зауважимо, що графіком будь-якої лінійної функції є деяка площина у трьохвимірному просторі.

Приклад .

x z y 0

Графіком функції є так званий параболоїд обертання. Ця поверхня утворюється, якщо обертати параболу або навколо осі . Як бачимо, накреслити графік функції не завжди просто. Більш простою геометричною ілюстрацією функції двох змінних є лінії рівня.

Лінії рівня.

Лінії рівня функції визначаються рівнянням , де – довільні сталі, узяті із множини значень функції.

Лінії рівня отримуються проектуванням на площину перетинів графіка функції площинами і лежать в області визначення функції . Лінії рівня не перетинаються і вздовж них функція залишається сталою.

Сукупність усіх ліній рівня називається картою ліній рівня.

Приклад . Для функції лінії рівня визначаються рівнянням або , де . Карта ліній рівня – множина паралельних прямих (див.рис.).

у х 0

При При При При

Приклад . Для функції лінії рівня визначаються рівнянням , де . Карта ліній рівня – множина концентричних кіл з центром в точці і радіусом .

у х 0 С = 4 С = 1 С = 0

При : – єдина точка . При : – коло . При : – коло .