Властивості визначеного інтеграла, які виражаються рівностями.

1. .

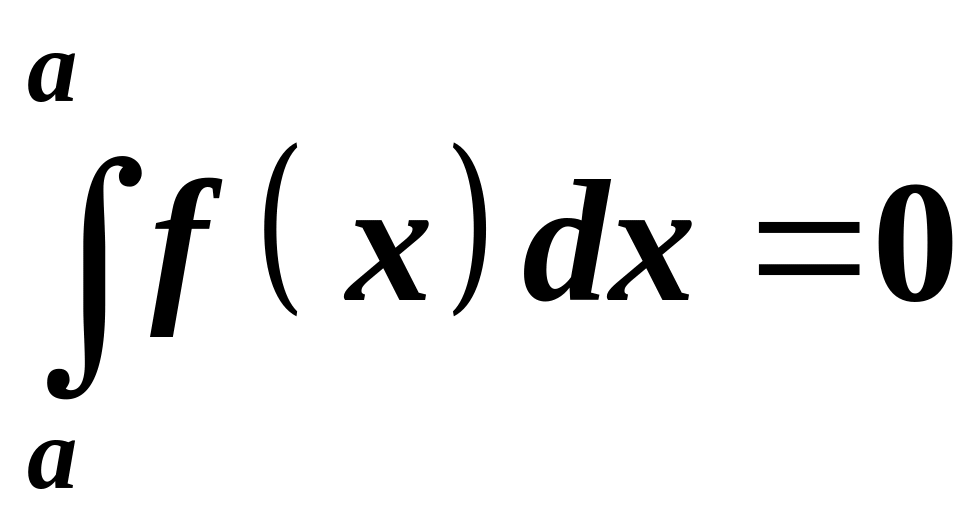Доведення. За теоремою Ньютона-Лейбніца: .

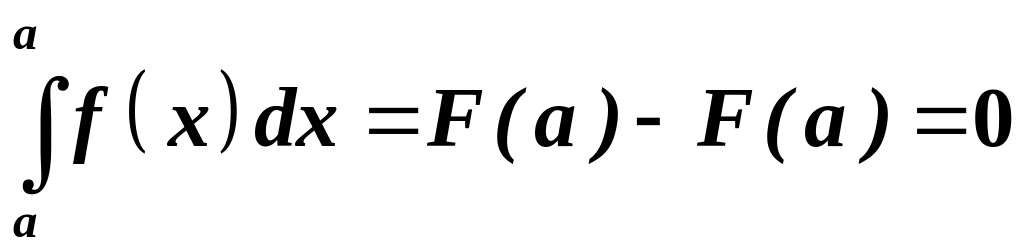2. .

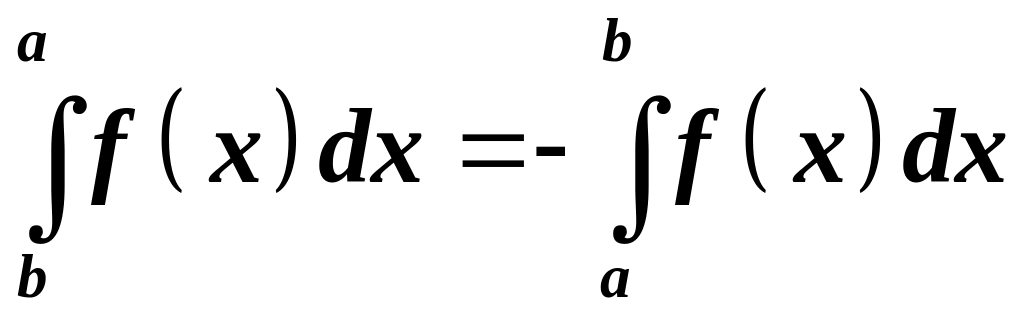Доведення. За теоремою Ньютона-Лейбніца:

.

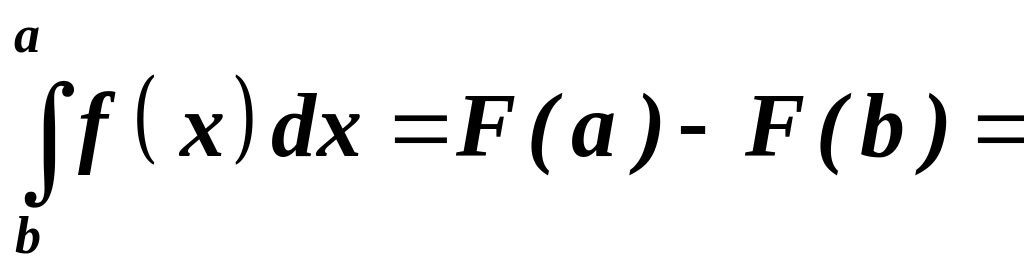
3. 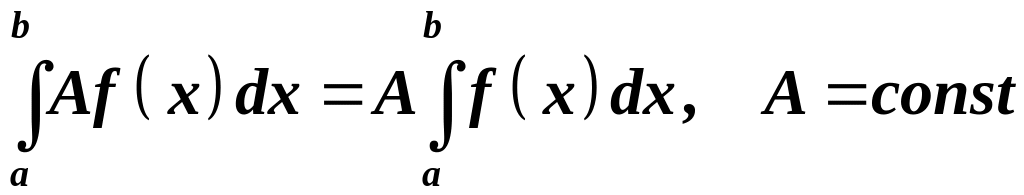. Тобто, сталий множник виноситься за знак визначеного інтеграла.

Доведення. За теоремою Ньютона-Лейбніца і властивістю невизначеного інтеграла:

.

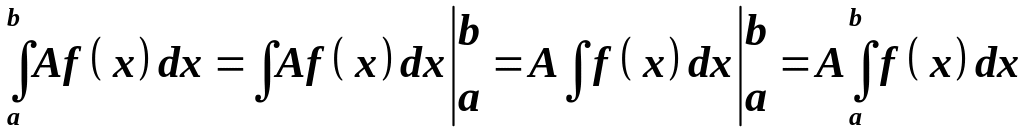4. .

Доведення. За теоремою Ньютона-Лейбніца і властивістю невизначеного інтеграла:

.

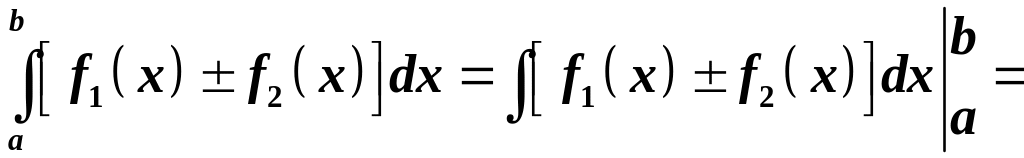
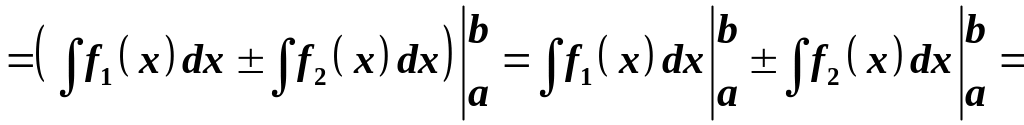
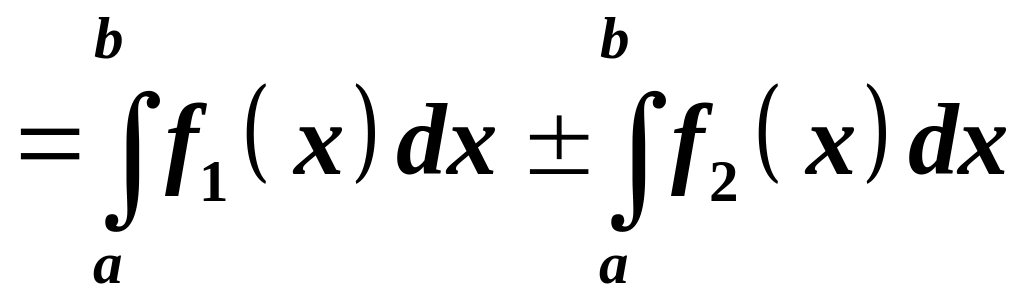5. 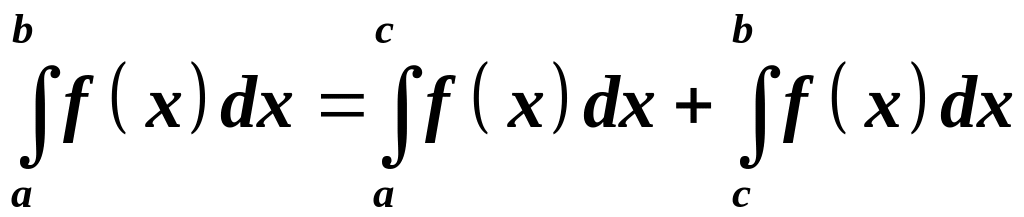. Ця властивість виконується при довільному розташуванні точок і називається аддитивністю визначеного інтеграла.

Доведення. За теоремою Ньютона-Лейбніца:

.

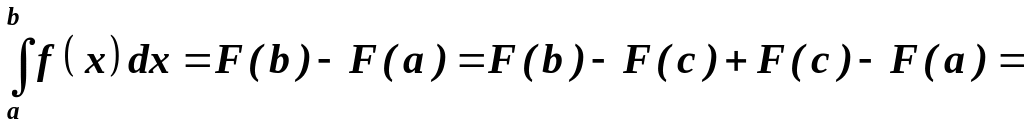
6. Теорема про середнє значення. Якщо функція неперервна на відрізку , то існує точка така, що

.

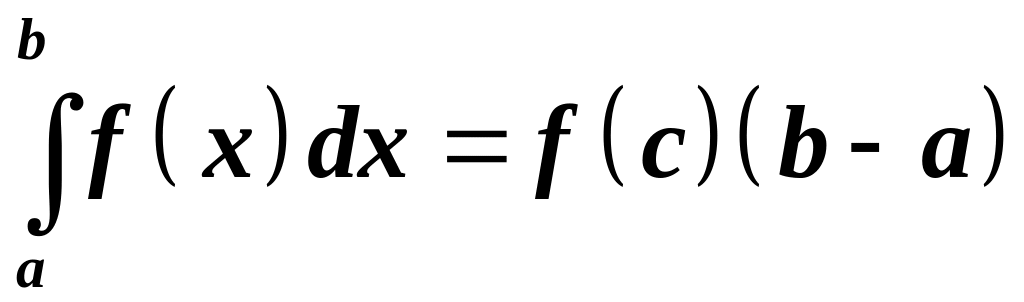З геометричної точки зору, ця теорема стверджує, що площа криволінійної трапеції, обмеженої лініями , , , , , дорівнює площі прямокутника з основою і висотою , де , тобто – деяка точка, розташована між і (див. рис.).

у

х 0 b с а

Властивості визначеного інтеграла, які виражаються нерівностями.

1. Якщо функція неперервна і на , то

.

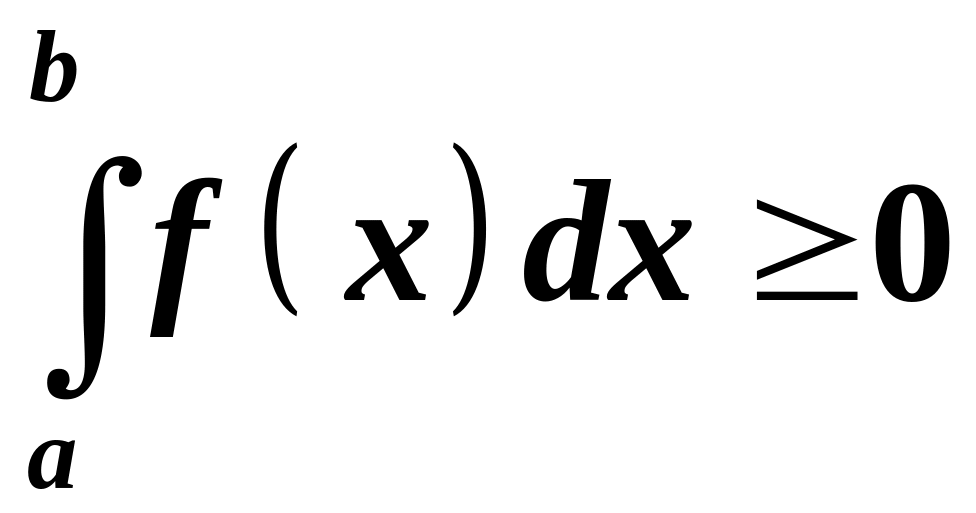Доведення властивості слідує із геометричного смисла визначеного інтеграла як площі криволінійної трапеції.

2. Якщо функції і неперервні і на відрізку , то

.

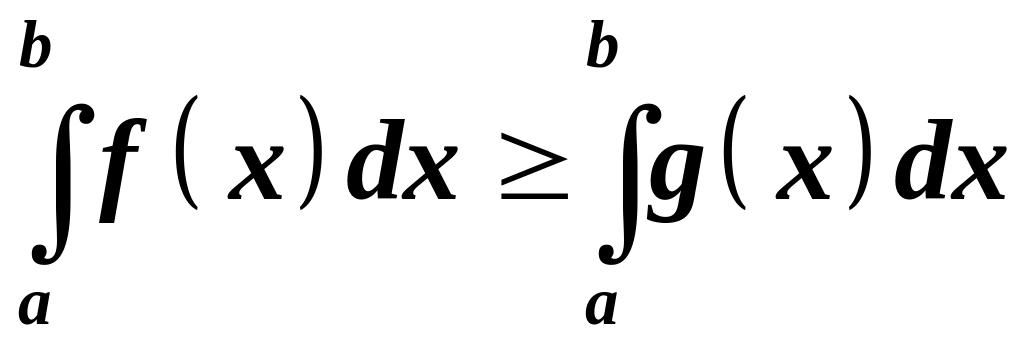Іншими словами, нерівності можна почленно інтегрувати.

Доведення. За попередньою властивістю для функції :

. Застосувавши властивість інтеграла від різниці функцій, дістанем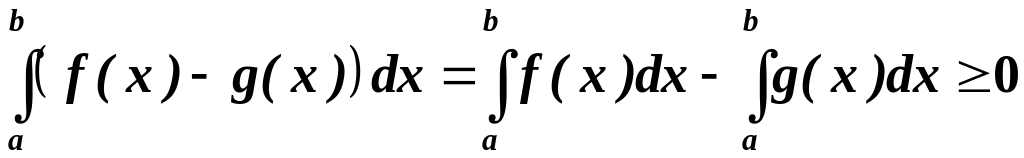о: або

, що і потрібно було довести.

При обчисленні визначених інтегралів застосовують ті ж самі методи, що і при знаходженні невизначених інтегралів. Розглянемо декілька прикладів безпосереднього інтегрування.

Приклад . Обчислити інтеграли:

а) .

Застосовуючи формулу Ньютона-Лейбніца, одержимо:

.

б) .

в) .

г) .

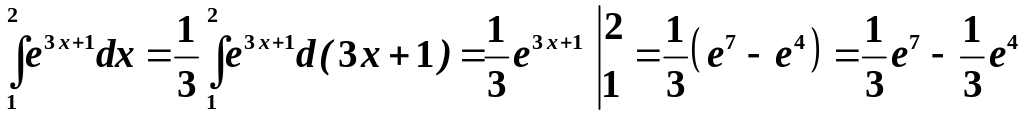д)

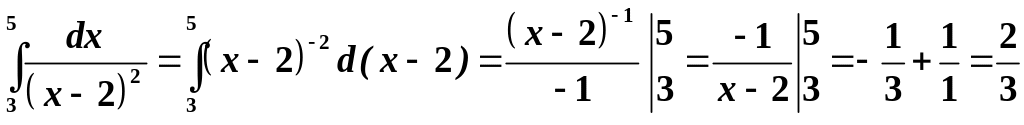
Метод інтегрування частинами.

Теорема. Нехай - неперервно диференційовні на функції. Тоді формула інтегрування частинами для визначеного інтеграла має вигляд:

.

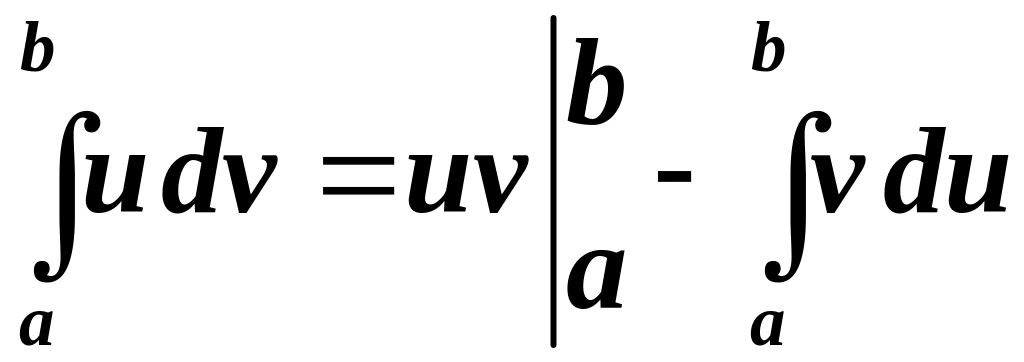Доведення. Використовуючи теорему Ньютона-Лейбніца та формулу інтегрування частинами для невизначеного інтеграла, отримуємо:

.

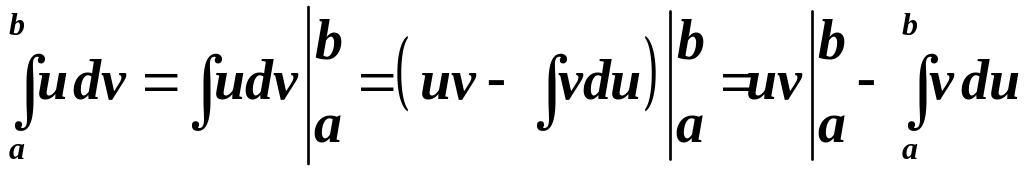Зауваження. Усі рекомендації відносно вибору і розглянуті для невизначеного інтеграла, застосовуються і для визначеного інтеграла.

Приклад . Обчислити інтеграл .

Розв’язування. Підінтегральна функція є добутком многочлена на показникову функцію, тому:

.

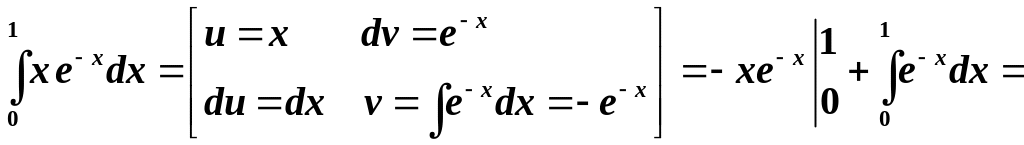
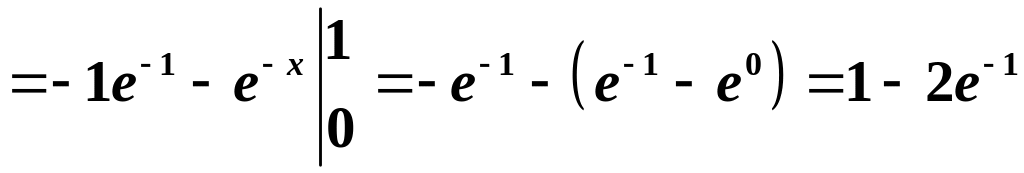Метод заміни змінної.

Теорема. Нехай функція - неперервна на , а - неперервно диференційовна на функція, причому , і на сегменті задана складена функція . Тоді формула заміни змінної у визначеному інтегралі має вигляд:

.

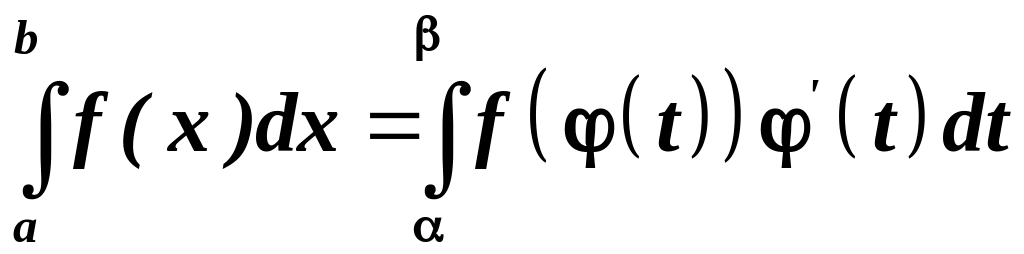Доведення. Нехай - первісна для функції на . Тоді за умовами теореми буде первісною для функції на . Користуючись теоремою Ньютона-Лейбніца, порівняємо ліву і праву частини формули.

Ліва частина: .

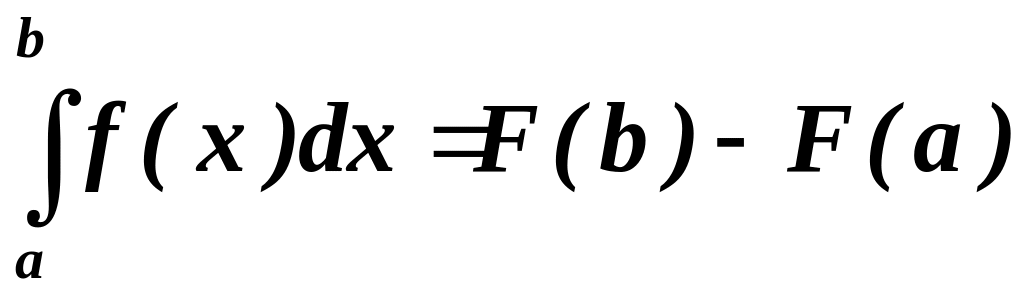Права частина: .

Теорема доведена.

Зауваження. На відміну від невизначеного інтеграла при заміні змінних у визначеному інтегралі не потрібно повертатись до вихідної змінної, але обов’язково необхідно змінювати межі інтегрування.

Приклад . Обчислити інтеграл .

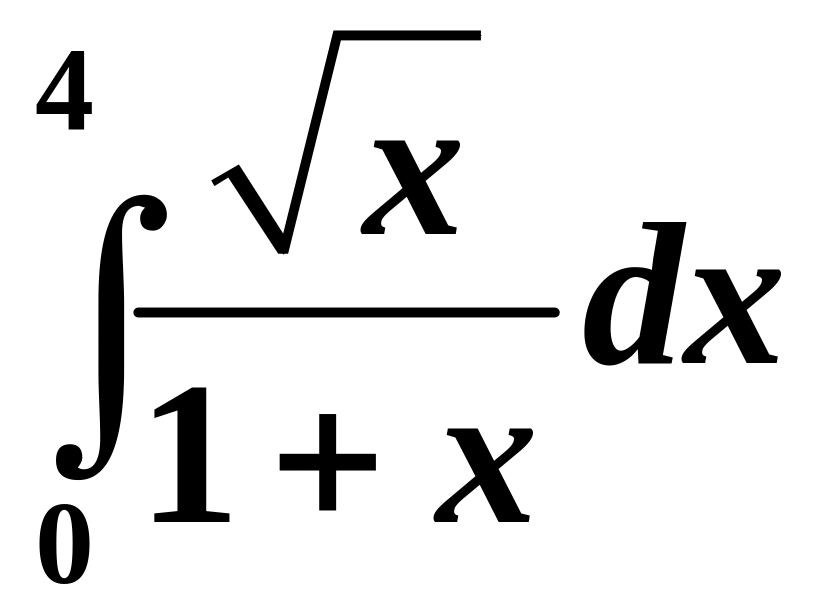Розв’язування.

.
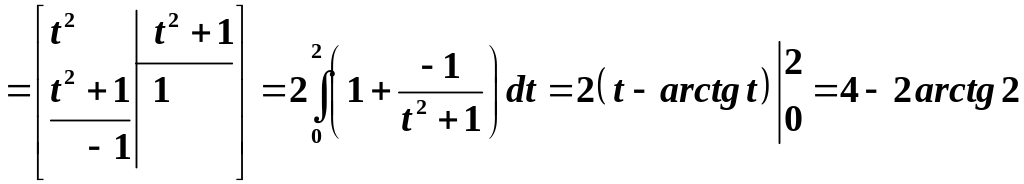