Найбільше і найменше значення функції в обмеженій замкненій області.

В обмеженій замкненій області неперервна функція завжди досягає свого найбільшого і найменшого значення (теорема Вейерштрасса), які можуть досягатись або в критичній точці усередині області, або на межі (границі) області.

Алгоритм розв’язування такої задачі є аналогічним знаходженню найбільшого та найменшого значень функції однієї змінної на замкненому проміжку - сегменті.

1. По заданих обмеженнях побудувати область .

2. Знайти критичні точки і обчислити значення функції в тих критичних точках, які належать області .

3. Знайти найбільше і найменше значення функції на на межі області .

4. Серед усіх знайдених значень функції вибрати найбільше і найменше.

Приклад . Знайти найбільше та найменше значення функції в трикутнику, обмеженому прямими , , .

Розв’зування.

1. Побудуємо заданий трикутник ОАВ – геометричний образ області (див. рис.)

4 О В х у А 1,4 2

2. Знайдемо критичні точки: Критична точка і .

3. Знайдемо найбільше і найменше значення на межі (границі) заданої області , яка складається із трьох сторін трикутника: ОА, АВ і ОВ.

На стороні оа , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .

; ; критична точка і .

На кінцях відрізка ОА: ; .

Отже, на стороні ОА найменше значення , а найбільше - .

На стороні ав або , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .

, , критична точка і .

На кінцях відрізка:

; .

Отже, на стороні АВ найменше значення , а найбільше - .

На стороні ов , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .

; ; критична точка і .

На кінцях відрізка: ; .

Отже, на стороні ОВ найменше значення: , а найбільше: .

Порівнюючи значення функції в точках , , , , , , :

; ; ; ;

; ; ,

робимо висновок: найбільше значення, яке дорівнює , функція набуває на межі області в точці , а найменше значення, яке дорівнює , функція набуває всередині області в точці .

Зауваження. Якщо функція - лінійна, то її графіком є деяка площина у просторі , а область задається системою лінійних нерівностей, які визначають опуклий многокутник на площині , то критичних точок всередині, а також на межі області не існує (не існує точок, в яких ). Тому лінійна функція набуває своїх найбільшого і найменшого значень тільки в точках, які є вершинами многокутника.

Наприклад, знайти найбільше та найменше значення функції в прямокутнику .
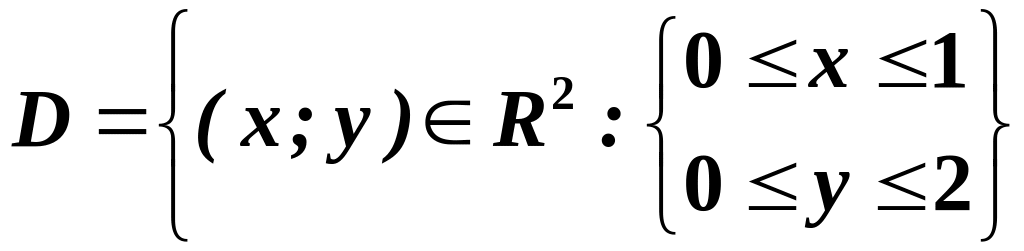