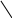Градієнт.

Серед усіх напрямків, що виходять із даної точки, виділяють особливий – так званий градієнтний.

Означення. Градієнтом функції у точці називається вектор, координатами якого є значення частинних похідних у цій точці.

Вектор градієнт позначається .

Очевидно, що в кожній точці області визначення функції, в якій існують частинні похідні, можна визначити такий вектор.

Найважливіші властивості градієнту:

1. Градієнт вказує напрямок найбільш швидкого зростання (а протилежний йому (антиградієнт)– найшвидшого спадання) функції, а його модуль визначає величину цієї швидкості.

2. є вектором нормалі до лінії рівня 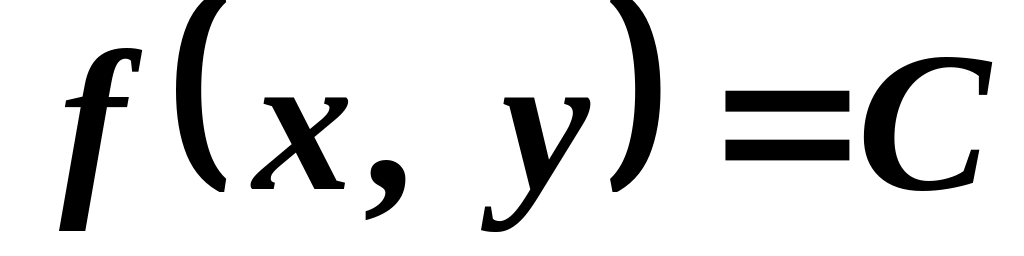, яка проходить через точку .

Приклад . Для функції знайти напрям із точки , у якому швидкість зростання функції максимальна (вектор-градієнт). Визначити довжину градієнта, схематично побудувати на координатній площині цей вектор та відповідну лінію рівня.

Розв’язування. Напрям, у якому швидкість зростання функції максимальна, визначає вектор-градієнт. Знайдемо його за формулою:

.

.

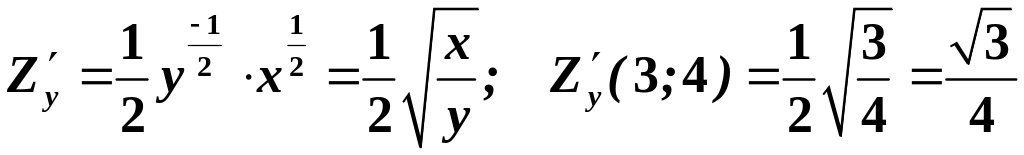Отже, . Довжина градієнта:

. Отже, в точці у напрямку градієнта функція зростає найшвидше (а у протилежному напрямку спадає найшвидше) зі швидкістю 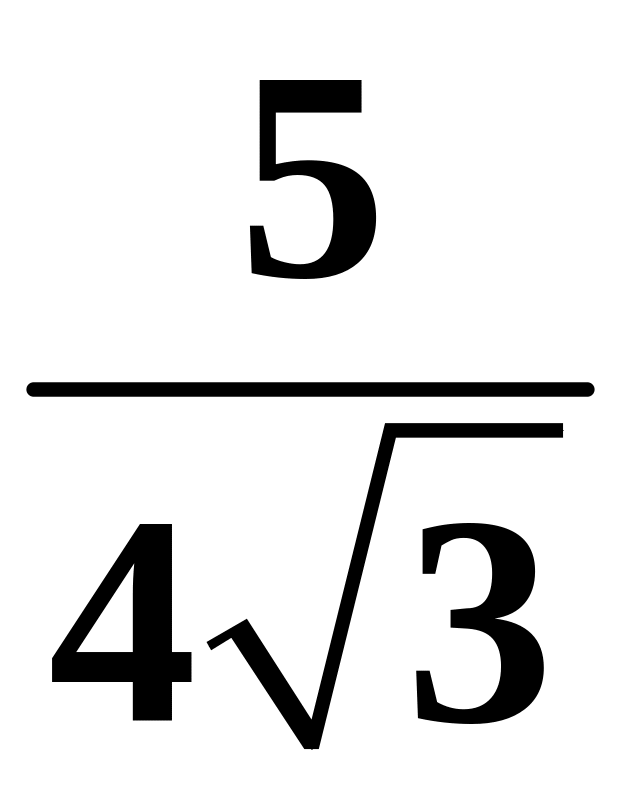Оскільки , то лінія рівня функції, що проходить через точку визначається рівнянням , або , або 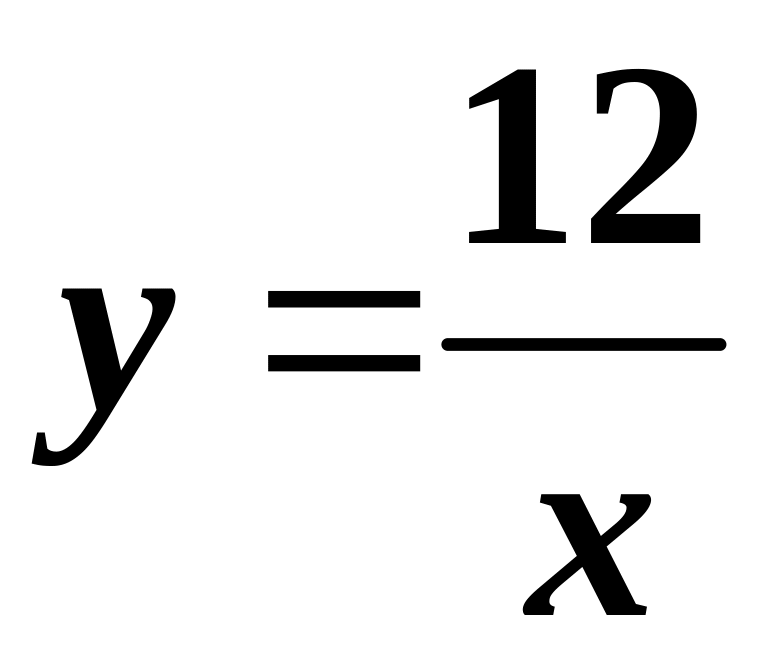. Це рівняння рівнобічної гіперболи (точніше - її вітка, яка розташована у першій чверті координатної площини ).

Зауваження 1. Вектор-градієнт використовують для пошуку екстремумів ФДЗ (зокрема, у математичному програмуванні).

Зауваження 2. Якщо функція лінійна , то її частинні похідні і є сталі величини і вектор-градієнт має незмінний напрямок у кожній точці області визначення функції.

Приклад . Для функції знайти напрямок, у якому швидкість зростання функції максимальна. З’ясувати геометричний зміст розв’язку.

Розв’язування. Знайдемо градієнт:

; ; або .

Лінії рівня даної функції визначаються рівнянням або .

При або .

При або .

При або .

Зобразимо градієнт і лінії рівня на координатній площині.

2 у 4 6 1 2 3 х 0 с = 3 с = 5 с = 7

Довжина градієнта . Найбільша швидкість зростання функції у будь-якій точці площини дорівнює , напрямок найбільшого зростання задає вектор градієнт .

Частинні похідні вищих порядків.

Якщо функція має частинні похідні першого порядку і , то у загальному випадку вони є функціями змінних та і, у свою чергу, також можуть мати частинні похідні, які називаються частинними похідними другого порядку і позначаються:

, читається : «де два зет по де ікс двічі»;

, читається : «де два зет по де ікс, де ігрек»;

, читається : «де два зет по де ігрек двічі»;

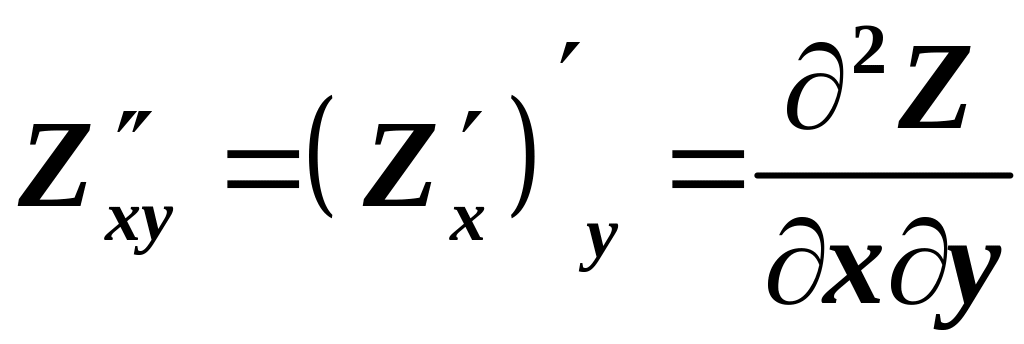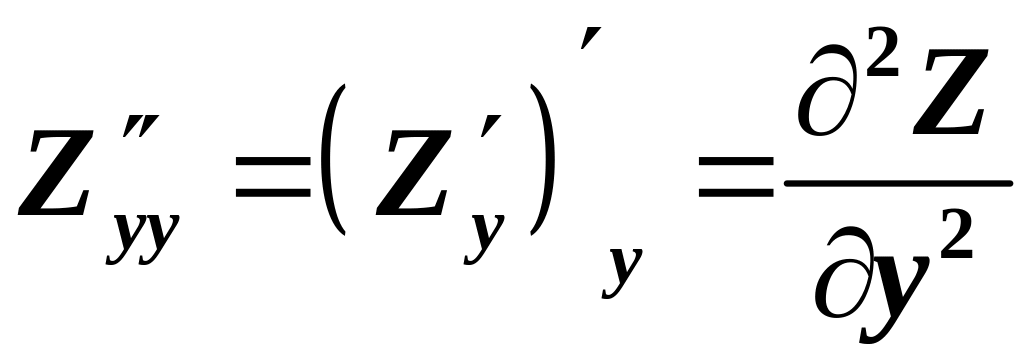, читається : «де два зет по де ігрек, де ікс»;

і називаються мішаними похідними другого порядку. Аналогічно визначаються похідні більш високих порядків.

Схематично процес утворення похідних можна зобразити наступним чином:

Відзначимо, що кількість частинних похідних подвоюється зі збільшенням на одиницю порядка похідної.

Приклад . Знайти частинні похідні другого порядку функції

.

Розв’язування.

;	;	;
;	;	;

Співпадання мішаних похідних не випадкове.

Справедлива теорема Шварца (про рівність мішаних похідних). Якщо мішані похідні другого порядку і існують і неперервні в точці , то в цій точці вони співпадають .

Аналогічно диференціалу першого порядку визначаються диференціали більш високих порядків. Наприклад, повний диференціал другого порядку функції двох змінних має вигляд (за умови існування і неперервності усіх похідних):

.

Відмітимо, що повний диференціал другого порядку може бути поданим у вигляді квадратичної форми від диференціалів (приростів) аргументів:

,

де - так звана матриця Гессе, визначник якої називають Гессіаном.

Диференціали другого порядку використовуються при дослідженні ФДЗ на екстремуми.