Розділ 2. Інтегральне числення

НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ

Поняття первісної та невизначеного інтеграла.

При вивченні основ диференціального числення функцій однієї змінної застосовувалась операція диференціювання, яка полягає в тому, що за заданою функцією ми знаходили її похідну або диференціал . В інтегральному численні розв’язується обернена задача – знаходження функції за заданою її похідною або заданим диференціалом . Таку задачу називають інтегруванням функції , а знайдену функцію називають первісною (антипохідною).

Означення. Функція називається первісною для функції на деякій множині (на деякому проміжку), якщо для усіх із цього проміжку, тобто, виконується тотожність .

Наприклад, для первісними будуть функції:

; ; ; і взагалі, , де - довільна стала.

Приклад показує, що на відміну від операції диференціювання, результат якої є однозначним, операція інтегрування дає цілу множину первісних.

Теорема (про множину первісних). Множина усіх первісних для даної функції задається формулою: , де - деяка первісна, а – довільна стала.

Доведення. По-перше, є первісною при будь-якій сталій . Дійсно, за означенням .

По-друге, будь-яку первісну можна отримати із формули при певному значенні сталої. Нехай – деяка первісна для функції . Тоді первісні і мають рівні похідні:

та .

За наслідком із теореми Лагранжа функції та можуть відрізнятись лише на сталу, тобто . Звідси . Теорему доведено.

Означення. Множина усіх первісних для даної функції називається невизначеним інтегралом від функції і позначається:

.

Тут – знак інтеграла, – підінтегральна функція; – підінтегральний вираз, – змінна інтегрування.

Знаходження невизначеного інтеграла називається інтегруванням функції.

Теорема (про існування невизначеного інтеграла). Якщо функція неперервна на деякому проміжку, то на цьому проміжку існує первісна для функції та невизначений інтеграл:

.

Таблиця основних інтегралів.

1. .

2. 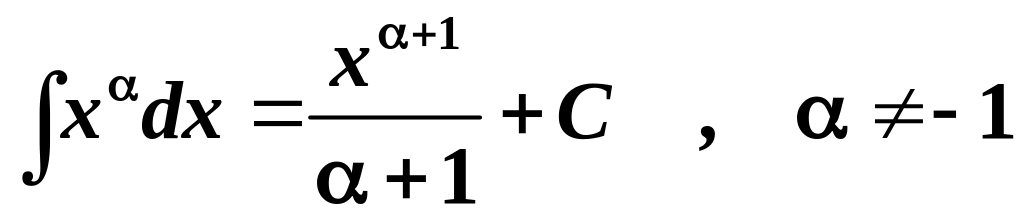. Зокрема, .

3. .

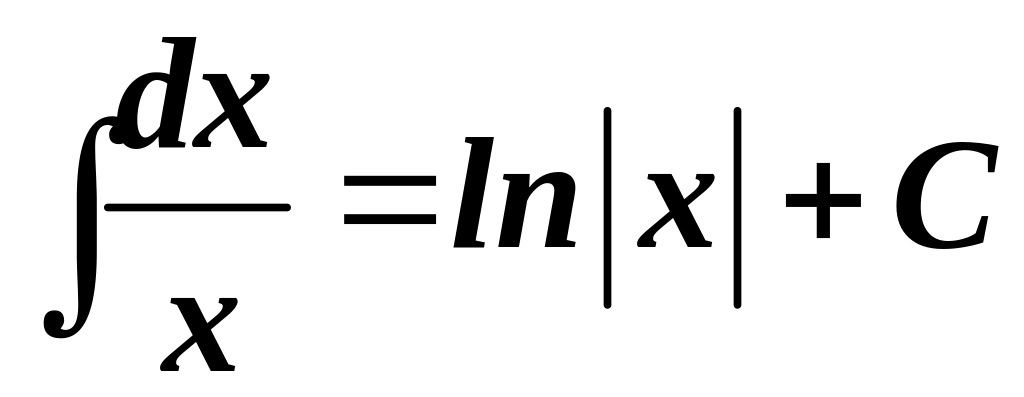4. 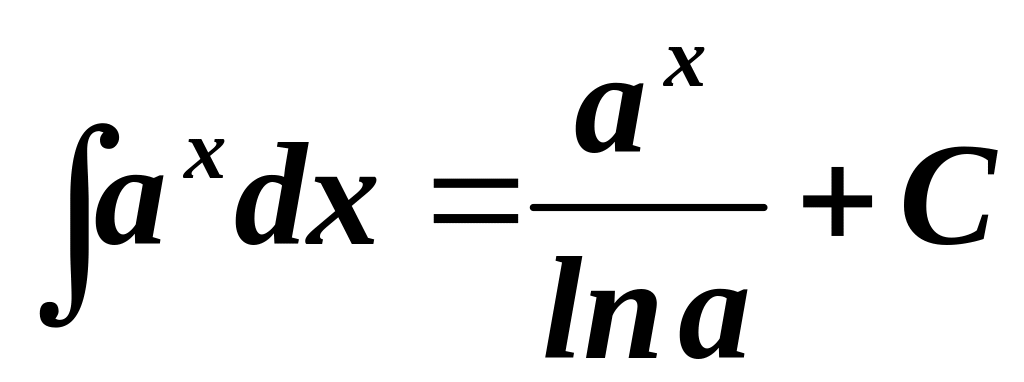. Зокрема, .

5. .

6. .

7. .

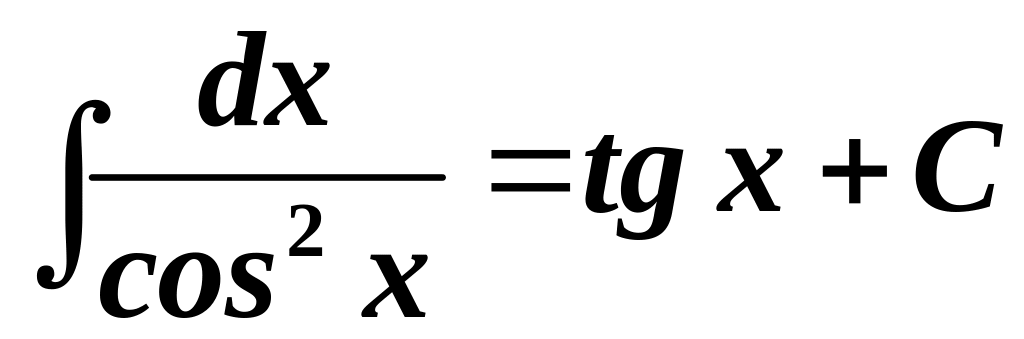8. .

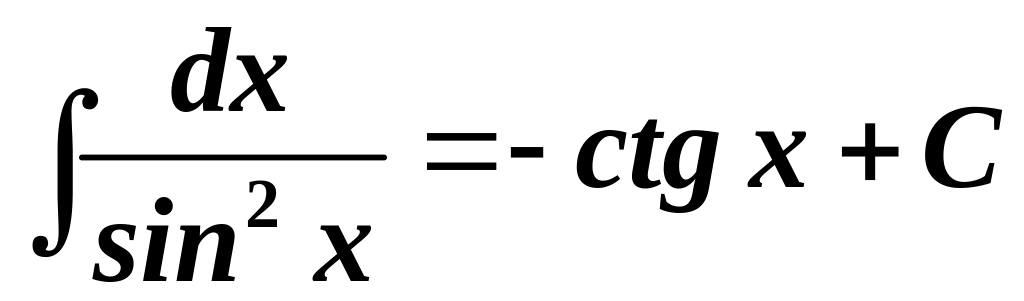9. .

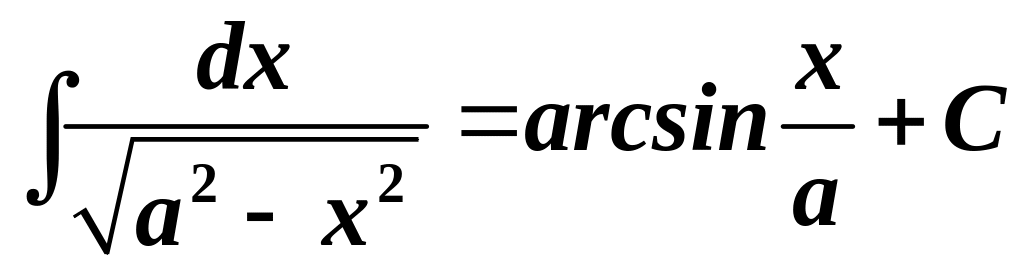10. .

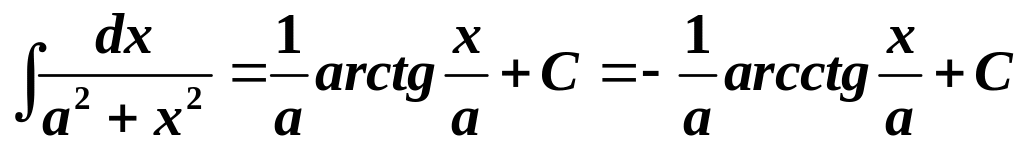11. .

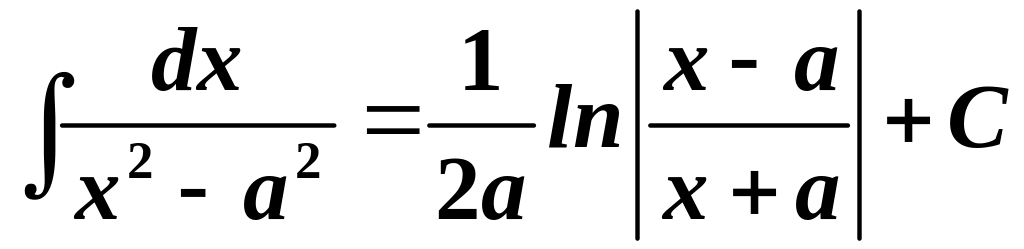12. .

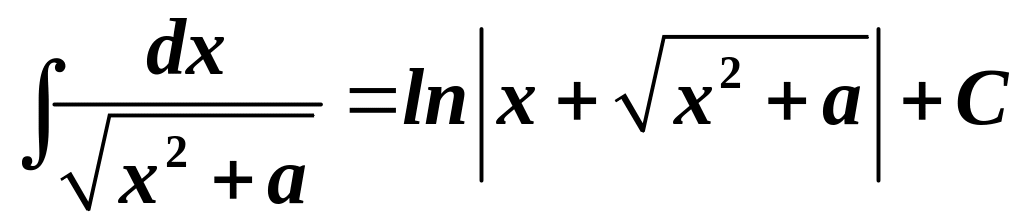Справедливість формул перевіряється шляхом диференціювання: похідні від правих частин формул дорівнюють відповідним підінтегральним функціям (фактично, майже усі табличні інтеграли – це антипохідні).

Доведемо, наприклад, останню формулу:

.

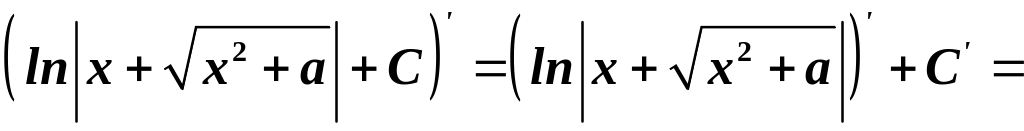
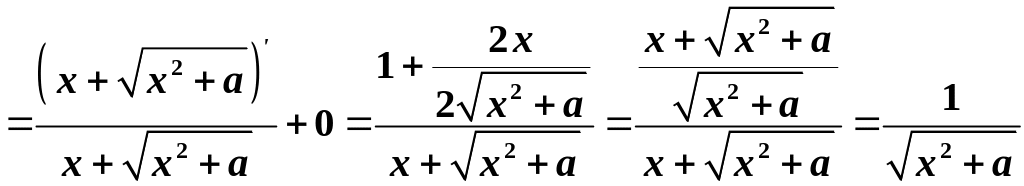Основні властивості невизначеного інтеграла.

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції.

.

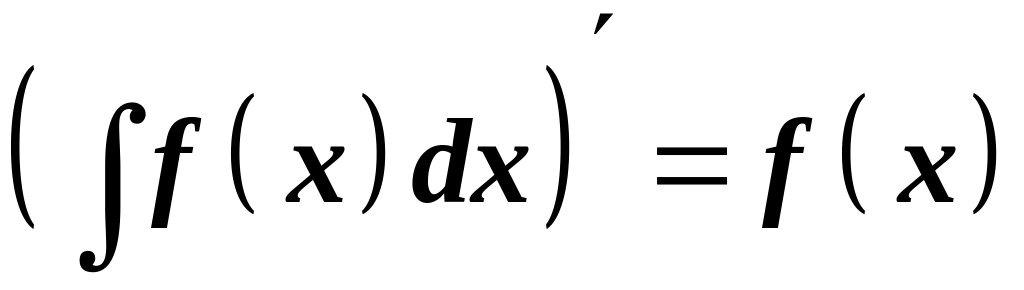Доведення: .

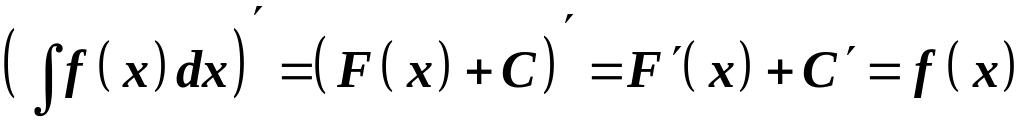Зауважимо, що дана властивість використовується для перевірки правильності знаходження інтегралів.

2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.

.

Доведення: .

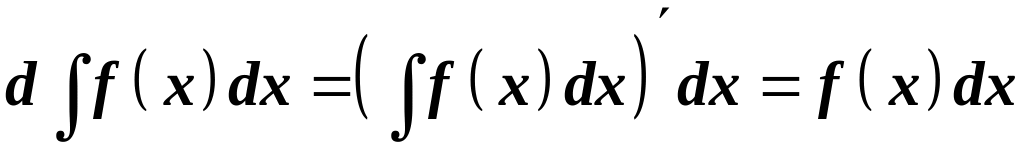3. Невизначений інтеграл від диференціала функції дорівнює самій функції плюс стала величина .

.

Доведення. Оскільки ліва і права частини рівності можуть відрізнятись на сталий доданок, то для доведення достатньо показати, що співпадають похідні обох частин:

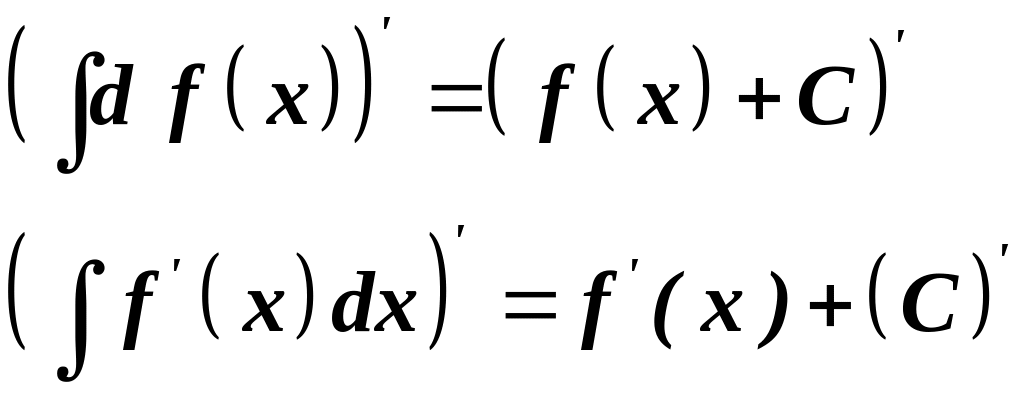
За властивістю 1: . Влативість 3 доведено.

4. Сталий множник виноситься за знак невизначеного інтеграла.

.

Доведення. Аналогічно доведенню попередньої властивості покажемо рівність похідних від обох частин рівності, скористувавшись властивостями 1 інтегралів та винесенням сталого множника за знак похідної:

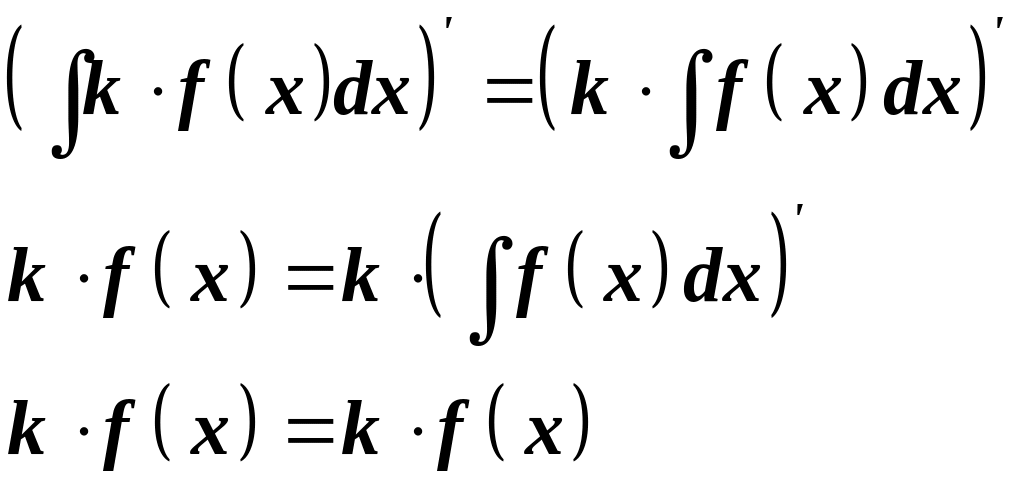
Властивість доведено.

5. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі інтегралів від цих функції.

.

Доведемо рівність похідних від обох частин рівності:

.

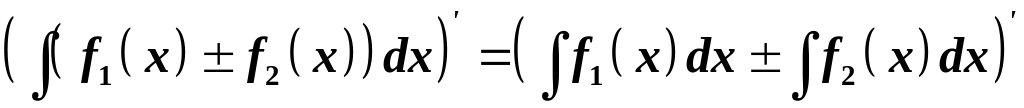Враховуючи першу властивість і похідну від алгебраїчної суми функцій, отримуємо:

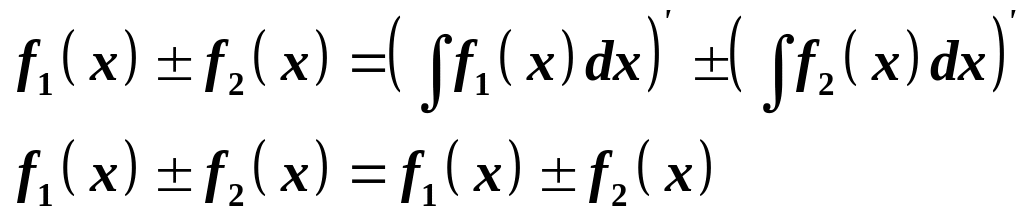
6. Властивість інваріантності форми невизначеного інтеграла:

,

де – будь–яка диференційовна функція, - первісна для функції .

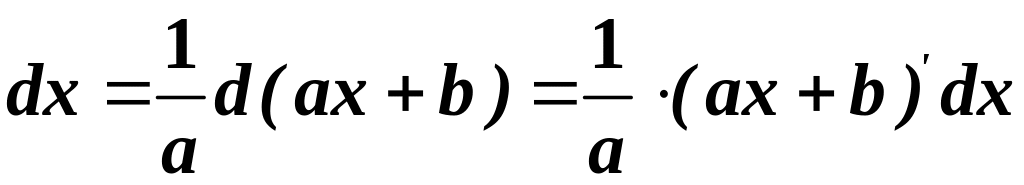Властивість інваріантності часто використовується при зведенні інтегралів до табличних. Наприклад, замість у підінтегральному виразі легко отримати диференціал будь-якої лінійної функції. Дійсно, оскільки , то:

.

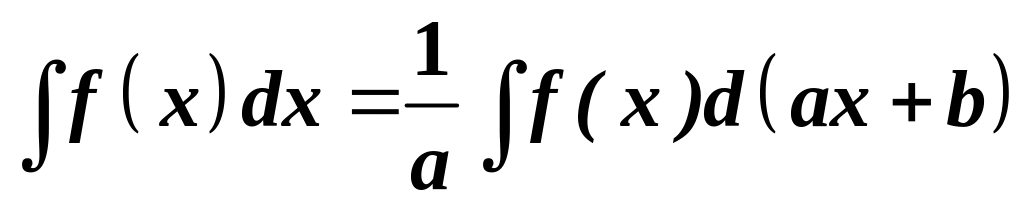Також досить часто зустрічаються інтеграли, в яких підінтегральна функція – дріб, чисельник якого дорівнює похідній знаменника. У таких випадках:

.
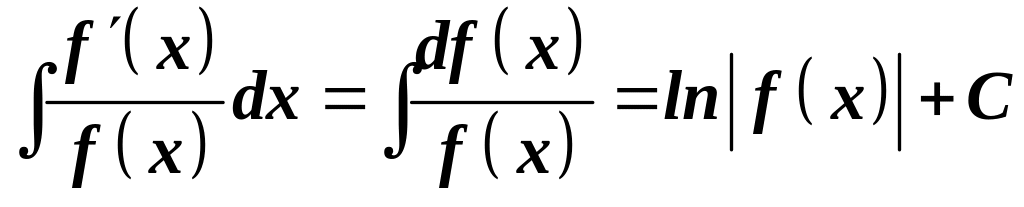