Решение:

Радиус сходимости R степенного ряда равен пределу отношения при условии, что этот предел (конечный или бесконечный) существует:

Здесь а_n= , a_n+1=

Имеем:

=

Радиус сходимости равен 1. Промежуток сходимости есть (-2-1; -2+1) или (-3; -1).

Внутри этого промежутка ряд сходится, вне его – расходится.

При х=-3 ряд принимает вид:

,

и он расходится согласно интегральному признаку сходимости для положительных рядов, так как каждый член положительного ряда меньше предшествующего и несобственный интеграл расходится, равен :

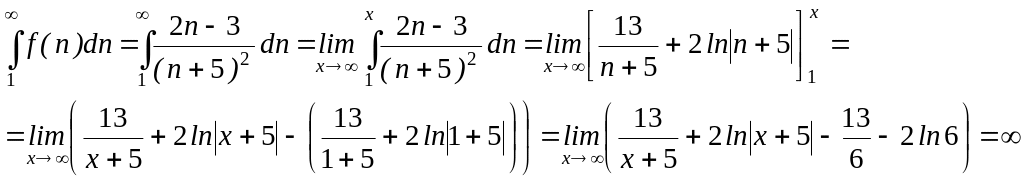
Следовательно, х=-3 не принадлежит области сходимости данного ряда.

При х=-1 ряд принимает тот же вид:

,

и он расходится согласно интегральному признаку сходимости для положительных рядов.

Следовательно, х=-1 не принадлежит области сходимости данного ряда.

Итак, (-3; -1) - область сходимости данного ряда.

Ответ: (-3; -1).

Найти область сходимости ряда

Решение:

Радиус сходимости R степенного ряда равен пределу отношения при условии, что этот предел (конечный или бесконечный) существует:

Здесь а_n= , a_n+1=

Имеем:

=

R=⁶/₇

Радиус сходимости равен ⁶/₇.

Промежуток сходимости есть (-⁶/₇; ⁶/₇). Внутри этого промежутка ряд сходится, вне его – расходится.

При х=-⁶/₇ ряд принимает вид:

,

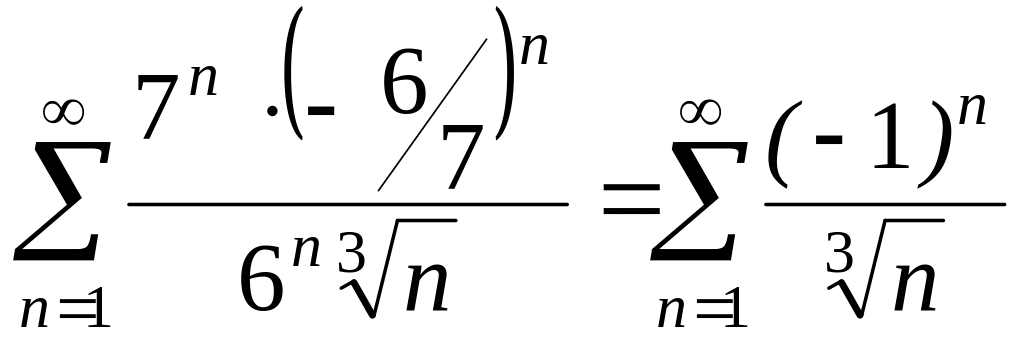и он сходится согласно признаку Лейбница для знакопеременных рядов (так как члены его стремятся к нулю, всё время убывая по абсолютному значению).

Следовательно, х=-⁶/₇ принадлежит области сходимости данного ряда.

При х=⁶/₇ ряд принимает вид:

,

и он расходится по признаку сравнения положительных рядов (так как члены исследуемого ряда не меньше соответствующих членов расходящегося гармонического ряда )

Следовательно, х=⁶/₇ не принадлежит области сходимости данного ряда.

Итак, [-⁶/₇; ⁶/₇) - область сходимости данного ряда.

Ответ: [-⁶/₇; ⁶/₇).

92. Разложение функций в степенной ряд

Разложить функцию f(x) в степенной ряд, расположенный по степеням х - х₀ – это значит составить ряд, у которого радиус сходимости не равен нулю, а сумма тождественно равна данной функции всюду внутри промежутка сходимости.

Если функция f(x) разлагается в степенной ряд, то разложение единственно.

Разложение простейших функций по степеням х:

• показательные (2);

• тригонометрические (4);

• гиперболические (4);

• логарифмические (2);

• биномиальные ряды (6);

• обратные тригонометрические (4);

• обратные гиперболические (4).