Лекция 22. Ряды.

92. Понятие числового ряда.

Пусть дана числовая последователь­ность а₁, а₂, а₃, ..., а_n, ... Выражение вида

называется числовым рядом или просто рядом. Числа а₁, а₂, а₃, ..., а_n ... называются членами ряда, член а_n с про­извольным номером — общим членом ряда. Суммы конечного числа членов ряда

S₁=а₁, S₂=а₁+а₂, S₃=а₁+а₂+а₃,…, S_n=а₁+а₂+а₃+…+а_n,

называются частичными суммами ряда.

Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм S₁, S₂, S₃, ..., S_n, ...

Ряд называется сходящимся, если последовательность его частичных сумм сходится к какому-нибудь числу S, которое в этом случае называется суммой ряда. Это запи­сывается так:

Ряд называется расходящимся, если последовательность его частичных сумм расходится.

Геометрическая прогрессия: b_n=b₁·q^n-1

;

Частичная сумма S_n, при q1 имеет вид:

• Если |q|<1, то - ряд сходится;

• Если |q|1, то - ряд расходится.

Геометрическая прогрессия:

b_n=b₁·q^n-1; ;

Частичная сумма S_n, при q1 имеет вид:

Если |q|<1, то , то ряд сходится;

Если |q|1, то , то ряд расходится.

1. Написать пять первых членов ряда. Вычислить пять частичных сумм. Исследовать ряд на сходимость:

Данный ряд расходится, так как последовательность его частичных сумм имеет бесконечный предел.

Данный ряд_____________________, так как последовательность его частичных сумм имеет_________________________________.

92. Свойства сходящихся рядов.

• Если сходится ряд: 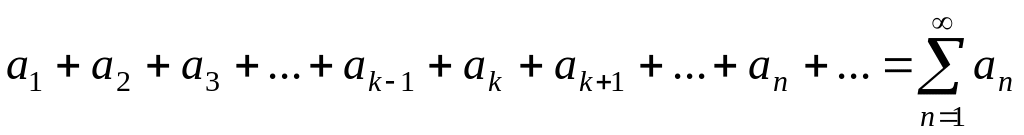, то сходится и ряд: 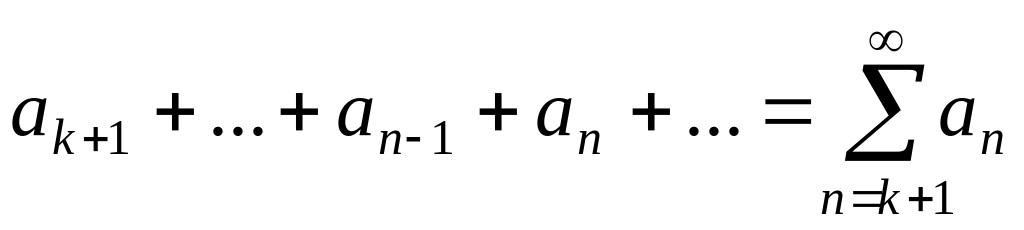, и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы:

• Если сходится ряд: и его сумма равна S, то и ряд 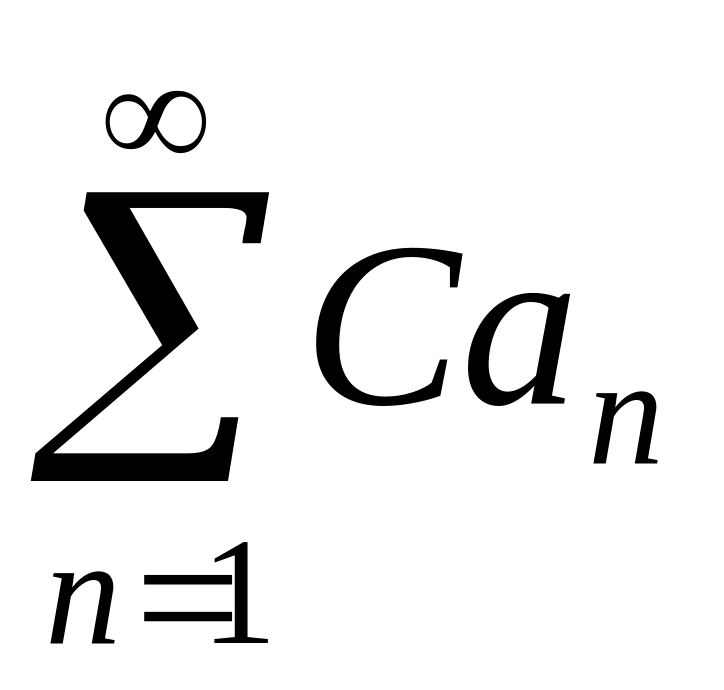где С=const, сходится и его сумма равна СS.

• Если сходятся ряды: и и их суммы равны S_а и S_b, то и ряд 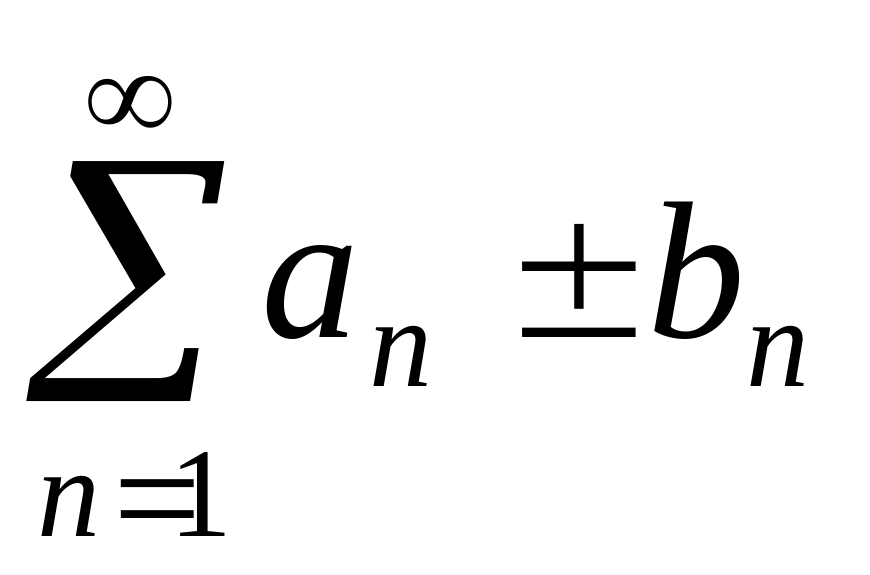, сходится и его сумма равна S_аS_b.

Необходимое условие сходимости ряда:

Если ряд сходится, то его общий член стремится к нулю, то есть .

Данное необходимое условие не является достаточным, а именно, если , то этого не достаточно для того, чтобы ряд сходился (например, гармонический ряд: вычислим предел его общего члена − но известно, что он расходится).

Достаточное условие расходимости ряда:

Если общий член ряда не стремится к нулю, то есть (или предела не существует), то ряд расходится.

Поэтому при исследовании ряда на сходимость вычисляем и если:

• , то вывод сделать невозможно, необходимо проводить дальнейшие исследования;

• (или предела не существует), то делаем вывод о том, что ряд расходится.

2. Написать первые пять членов ряда и исследовать ряд на сходимость:

Необходимое условие сходимости ряда выполняется: . Данный ряд является геометрической прогрессией, в которой Так как , то ряд сходится.	Необходимое условие сходимости ряда _________________: Данный ряд является геометрической прогрессией, в которой Так как , то ряд ________________.
Необходимое условие сходимости ряда выполняется: . Данный ряд является геометрической прогрессией, в которой Так как , то ряд сходится.	Необходимое условие сходимости ряда _________________: Данный ряд является геометрической прогрессией, в которой Так как , то ряд _______________.
Необходимое условие сходимости ряда _________________: ряд _______________.	Необходимое условие сходимости ряда _________________: ряд _______________.