Свойства

1. , если   — простое число. В частности, при   имеем  ;

2. , если   и   взаимно просты. То есть Функция Эйлера мультипликативна;

3. , если   и   взаимно просты. Так называемая теорема Эйлера;

4. 

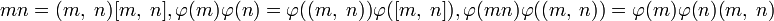5. , если   — наименьшее общее кратное, a   — наибольший общий делитель.

33. Теорема Эйлера и ее доказательства, малая теорема Ферма : примеры.

Теоре́ма Э́йлера в теории чисел гласит:

Если   и   взаимно просты, то  , где   — функция Эйлера.

Доказательства с помощью теории чисел

Пусть   — все различные натуральные числа, меньшие   и взаимно простые с ним.

Рассмотрим всевозможные произведения   для всех   от   до  .

Поскольку   взаимно просто с   и   взаимно просто с  , то и   также взаимно просто с  , то есть   для некоторого  .

Отметим, что все остатки   при делении на   различны. Действительно, пусть это не так, то существуют такие  , что

или

Так как   взаимно просто с  , то последнее равенство равносильно тому, что

 или  .

Это противоречит тому, что числа   попарно различны по модулю  .

Перемножим все сравнения вида  . Получим:

или

.

Так как число   взаимно просто с  , то последнее сравнение равносильно тому, что

или

 

Ма́лая теоре́ма Ферма́ — классическая теорема теории чисел, которая утверждает, что

Если p — простое число, и   не делится на  , то   Другими словами,   при делении нацело на   даёт в остатке 1.

Равносильная формулировка:

Для любого простого   и целого  :  делится на

Свойства и некоторые следствия

• Если   — простое число, а   и   — такие положительные целые числа, что  , тогда  . Это утверждение используется в системе шифрования с открытым ключом RSA.

• Если   — простое число, отличное от 2 и 5, то число  , запись которого состоит из одних девяток, делится на  . Отсюда легко следует, что для любого целого числа  , которое не делится на 2 и на 5, можно подобрать число, состоящее только из девяток, которое делится на   ^[1]. Этот факт используется в теории признаков делимости и периодических дробей.

34. Способы деления чисел в конечном простом поле: примеры.

35. Задача факторизации больших чисел и криптографическая система RSA. Общая схема и пример шифрования и дешифрования. Сложность факторизации числа.

Факториза́цией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики.

В отличие от задачи распознавания простоты числа, факторизация предположительно является вычислительно сложной задачей.

Применение в криптографии

Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA.

Всеобщий интерес к проблеме разложения на простые множители резко возрос в 1977 году, когда Р. Л. Райвест (R. L. Rivest), А. Шамир (A. Shamir) и Л. Адэлман (L. Adleman) разработали первую систему шифрования с открытым ключом, известную в настоящее время как RSA. В данной системе процедуры зашифрования и расшифрования выполняются на различных ключах. Знание только ключа зашифрования не позволяет расшифровать сообщение, поэтому он не является секретным элементом шифра и обычно публикуется, чтобы любой желающий мог отправить владельцу этого ключа шифрованное сообщение. Зная только открытый ключ, секретный ключ вычислить невозможно. Криптостойкость данной системы основана на трудности разложения больших целых чисел на простые множители. Так как до сих пор не найден эффективный алгоритм разложения чисел на простые множители, этот метод позволяет почти гарантированно защитить засекреченные данные и сообщения в компьютерной сети.

RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других.